Characterization of Exponential Distribution Through Normalized Spacing of Generalized Order Statistics
- DOI
- 10.2991/jsta.d.190818.004How to use a DOI?
- Keywords
- Continuous distribution; Generalized order statistics; Meijer's G-function; Characterization
- Abstract
In this paper, exponential distribution is characterized by normalized spacing of generalized order statistics (gos) using Meijer's G-function. While the necessary part of the theorem was given by U. Kamps, E. Cramer, Statistics. 35 (2001), 269–280, we have given an easy proof of sufficient part in this paper. This paper contains the result of characterization of exponential distribution through normalized spacing of order statistics, sequential order statistics, progressive type II censoring and record values. Also, by simulation study, we have shown that the confidence interval based on upper records is shorter in length than asymptotic confidence interval constructed by maximum likelihood estimate.
- Copyright
- © 2019 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Ordered random variables like order statistics, record values, sequential order statistics and progressive type II censored order statistics frequently arise in real life situations. For application of ordered random variables, one may refer to [1], to [2] for order statistics, to [3] and [4] for record values and to [5] for progressive type II censored order statistics and reference cited therein. The concept of generalized order statistics
Let
Let
Suppose
In this paper, we have extended the result of [16] and [14] and characterized the exponential distribution using normalized spacing of goss. While the necessary part of the main theorem was given by [20], in this paper, we have given a simple and easy proof for the sufficient part of the theorem. The paper is divided into four sections. In Section 2, based on
2 CHARACTERIZATION OF EXPONENTIAL DISTRIBUTION
In this section, exponential distribution has been characterized through the normalized spacing based on goss.
The following two Lemmas are given, which have been used in the proof of the theorem. Proof of the Lemmas are straightforward and hence omitted.
Lemma 2.1.
Let
Lemma 2.2.
Let
Theorem 2.1.
Let
Proof.
The necessary part was established by [20] as follows:
This implies that
To prove the sufficient part, we have for any positive and finite
Let
Integrating
Now, we know from [8] (p. 130), that
Let
Using (13) and (14) in (12), we get
This implies that
Now in view of Lemma 2.1 together with Lemma 2.2, we have
Since both
For
3 SIMULATION STUDY
Here we have followed the procedure adopted by [19] and carried out the simulation to construct the confidence interval for scale parameter
Let
To construct these confidence intervals we simulate 10,000 samples of size

Plot of confidence interval for θ = 0.2.
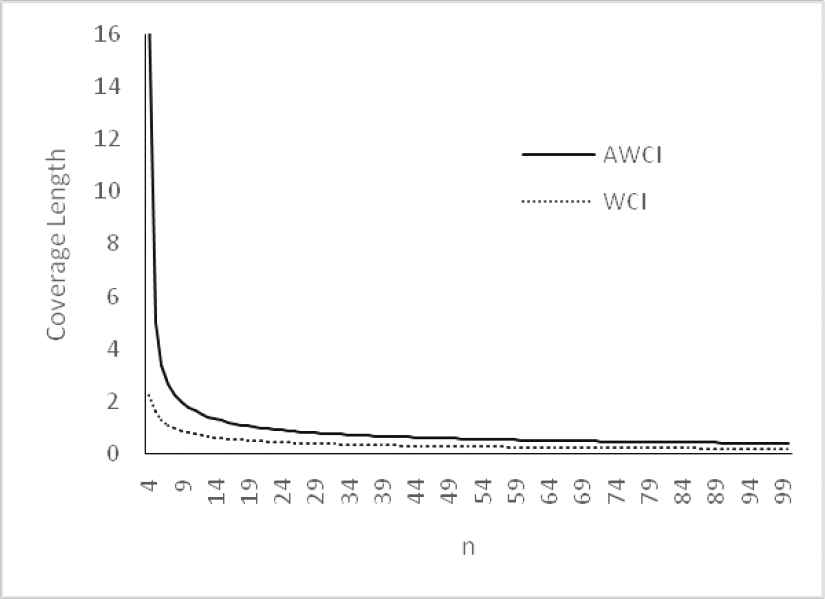
Plot of confidence interval for θ = 0.5.

Plot of confidence interval for θ = 1.

Plot of confidence interval for θ = 2.
4 CONCLUDING REMARK
In real life, a statistician is often interested in guessing the probability distribution from which the true data is obtained. Characterization problem is a theoretical approach to obtain the distribution function if certain conditions are fulfilled. A probability distribution can be characterized in many ways and the method under study here is one of them. Further this result may be used to ease statistical computation. For example, if we are computing moments of difference between two gos (order statistics, records, sequential order statistics, progressive type II censored order statistics), when the random variables
REFERENCES
Cite this article
TY - JOUR AU - M. J. S. Khan AU - S. Iqrar AU - M. Faizan PY - 2019 DA - 2019/09/02 TI - Characterization of Exponential Distribution Through Normalized Spacing of Generalized Order Statistics JO - Journal of Statistical Theory and Applications SP - 303 EP - 308 VL - 18 IS - 3 SN - 2214-1766 UR - https://doi.org/10.2991/jsta.d.190818.004 DO - 10.2991/jsta.d.190818.004 ID - Khan2019 ER -
