Optimization for Line of Cars Manufacturing Plant using Constrained Genetic Algorithm
In 2007 he obtained his PhD at the Department of Brain Science and Engineering, Kyushu Institute of Technology. From April, 2007 to March, 2014, he was a lecturer. Since April, 2014, he has been an associate professor, Nishinippon Institute of Technology.
- DOI
- 10.2991/jrnal.2018.5.2.13How to use a DOI?
- Keywords
- Constrained Genetic Algorithm; Plant Optimization; Industrial Application; Car manufacturing
- Abstract
Recently, improvement of production efficiency on cars manufacturers is required. However, that improvements under existing circumstances are depending on experience and intuition by workers. We propose to objectively and efficiently improve a production line based on a GA. The difficulty of applying a GA is the number of racks and boxes is predetermined, and so we apply constrained GA. The results of simulation for virtual production line show that our proposal succeeded in reducing about 10 seconds per a car compared with random positioning.
- Copyright
- Copyright © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Recently, improvement of production efficiency on cars manufacturers is required owing to increasing of demands in developing countries. On the other hand, that improvements under existing circumstances are depending on experience and intuition by workers at a production line1, 2. To overcome this situation, we propose to objectively and efficiently improve a production line without depending on experience and intuition. The production line of candidate for optimization is “Picking up assemblies” area, so that our aim is to optimize the positions of racks and boxes for assemblies. The difficulty of optimization of “Picking up assemblies” area is that the number of racks to put assembly boxes and that boxes is predetermined.
Our optimization problem is similar to several path planning problems such as “Traveling Salesman Problem (TSP),” “Minimum Spanning Tree problem(MST).” Workers pick up assemblies while they goes back and forth between racks and an AGV. Accordingly, our optimization problem becomes synonymous with minimization of total length of moving path of a worker. The difference between path planning problems and our problem is that positions of waypoints for path planning problems are fixed; on the other hand, our problem changes positions of waypoints that are racks and boxes.
Since the number of racks and boxes is predetermined as mentioned, our approach has to put predetermined number of racks and boxes into a production line. For this, there is also a problem of “Knapsack Problem(KP)” in our optimization problem. It can be said that our optimization problem combines TSP, MST and KP for the reasons stated above.
To overcome difficulties, we propose to apply a Genetic Algorithm(GA)3, 4 to optimization for positions of racks and boxes. A GA is suitable for global search in a high dimensional space because a GA has also the ability of probabilistic random search based on genetic operations in addition to local search. A GA has many individuals(populations), and an individual has a chromosome that cords the parameters for optimization. Optimization processes are on the basis of genetic operations, i. e., selection, crossover and mutation. A process of crossover and mutation does not be constrained because parameters for optimization in a chromosome are independent in each; therefore, generated parameters of optimization are able to take all values within a set condition. By contrast, parameters of optimization in our problem are dependent on each other because the number of racks to put assembly boxes and that boxes is predetermined. Consequently, we are not able to apply a conventional GA to optimization. For this, we apply a “constrained GA” to optimization for positions of racks and boxes in a production line.
The details of our constrained GA are below. Gene loci correspond to racks and boxes positions in a constrained GA. Selection process in genetic operations is same way as a conventional GA. In crossover process, loss or duplication of some racks and boxes will occur. The way of adjustment of the number of racks is that all of duplicative racks are deleted then missing racks are randomly inserted to those positions. Mutation process for racks is executed after the adjustment of crossover process. Mutation process in a constrained GA changes gene loci in order to meet the conditions for the number of racks. Crossover and mutation process for positions of boxes in racks is executed after crossover and mutation process for racks. Crossover process for boxes is executed on the same stage each other, e.g., boxes in top stage of a rack are changed with boxes in top stage of another rack. In mutation process, genes for boxes are mutated randomly as same as a conventional GA in first. Following that, excess boxes are randomly chosen, then those boxes are deleted. Subsequently, shortfall in boxes are inserted randomly to meet the conditions for the number of boxes. From a constrained GA in above, our proposal is able to meet the conditions for our optimization problem.
The results of simulation for virtual production line show that our proposal succeeded in reducing about 10 seconds per a car compared with random positioning.
2. Virtual Environment of Production Line
We construct a virtual environment of production line to validate the effectiveness of our proposal. Table 1 shows the conditions for virtual environment, and Table 2 shows the number of assembly boxes for each car.
| Kinds of Rack(Length) | 3(1000, 1500, 2000) |
| Stages in a Rack | 3(Top, Middle, Bottom) |
| Kinds of Assembly Boxes | 3 |
| Length of a Line | 15000 |
| Distance of AGV and Racks | 1500 |
| Moving Speed of AGV | 200[mm/s] |
| Walking Speed of a Worker | 2000[mm/s] |
| Number of racks | 1000×3, 1500×4, 2000×3 |
| Types of Cars(Car names) | 4(Car1, Car2, Car3, Car4) |
| Mixing Rate of Cars in Productions | Car1:0.5, Car2:0.25, Car3:0.15, Car4:0.1 |
Conditions of virtual environment. Length unit is millimeter.
| Width of assembly boxes | |||
|---|---|---|---|
| 300 | 600 | 1000 | |
| Car1 | 15 | 4 | 2 |
| Car2 | 15 | 3 | 1 |
| Car3 | 10 | 3 | 1 |
| Car4 | 10 | 0 | 1 |
| Shared | 30 | 5 | 5 |
Number of assembly boxes for each car. “300”,”600” and “1000” correspond to width of assembly boxes. Width unit is millimeter.
A worker in virtual environment picks up the all of assemblies which correspond to a designated car in the Table 2. Besides, 20 shared assemblies are randomly designated from the all of shared assemblies.
The Fig. 1 shows the bird’s-eye view of an example of virtual production line. The condition in that figure is initial state of picking up assemblies. A worker goes back and forth between racks and an AGV. An AGV moves at a constant speed on a lane.

Bird’s eye view of an example of virtual production line. Values are distance and size of rack. Unit is millimeter. The red circle indicates a worker. The blue, yellow and magenta squares correspond to 1000, 1500 and 2000 size of racks, respectively.
Consequently, our optimization problem is same as minimization of the moving distance of a worker.
3. Optimization Problem
From the above section, our optimization problem is similar to several path planning problems such as “Traveling Salesman Problem (TSP),” “Minimum Spanning Tree problem(MST).” Our optimization problem becomes synonymous with minimization of total length of moving distance of a worker. The difference between path planning problems and our problem is that positions of waypoints for path planning problems are fixed; on the other hand, our problem changes positions of waypoints that are racks and boxes in order to minimize length of moving distance.
In addition, since the number of racks and boxes is predetermined as mentioned in the table 1 and 2, our approach has to put predetermined number of racks and boxes into a production line. For this, there is also a problem of “Knapsack Problem(KP)” in our optimization problem. It can be said that our optimization problem combines TSP, MST and KP for the reasons stated above.
4. Genetic Algorithm and Constrained
To overcome difficulties mentioned in the section 3, we propose to apply a GA to optimization for positions of racks and boxes. We explain the details of a conventional GA, and of a constrained GA to solve our problem.
4.1. Genetic Algorithm
A Genetic Algorithm(GA) is suitable for global search in a high dimensional space because a GA has also the ability of probabilistic random search based on genetic operations in addition to local search. A GA has many individuals(populations), and an individual has a chromosome that cords the parameters for optimization. Optimization processes are on the basis of genetic operations, i. e., selection, crossover and mutation.
In a conventional GA, a process of crossover and mutation does not be constrained because parameters for optimization in a chromosome are independent in each; therefore, generated parameters of optimization are able to take all values within a set condition. On the other hand, parameters of optimization in our problem depend on each other because the number of racks and assembly boxes is predetermined. For this, we apply a “constrained GA” to optimization for positions of racks and boxes as mentioned in the next section.
4.2. Constrained Genetic Algorithm
We explain the details of a “constrained GA” in this section. Gene loci correspond to racks and to boxes positions in a constrained GA. Selection process in genetic operations is same way as a conventional GA. In crossover process, loss or duplication of some racks and boxes will occur. The way of adjustment of the number of racks is that all of duplicative racks are deleted then missing racks are randomly inserted to those positions. The Fig. 2 illustrates an example of the way of adjustment.

An example of crossover process for racks. P1, P2, C1 and C2 correspond to parent 1, 2 and child 1, 2, respectively. (a)Duplication and loss. (b)After adjustment.
Mutation process for racks is executed after the adjustment of crossover process. The Fig. 3 illustrates an example of mutation for racks.

An example of mutation process for racks. C1 and C2 correspond to child 1 and 2, respectively. Colored cells represent the mutated positions.
Mutation process in a conventional GA changes genes; by contrast, that process in a constrained GA changes gene loci in order to meet the conditions for the number of racks.
Crossover process for boxes is executed on the same stage each other, e.g., boxes in top stage of a rack are changed with boxes in top stage of another rack. In mutation process, genes for boxes are mutated randomly as same way as a conventional GA. Following those processes, the adjustment process in order to meet conditions is proceeded. Firstly, excess boxes that do not meet conditions in Table 2 are randomly chosen, then those boxes are deleted. Subsequently, shortfall in boxes are inserted randomly to meet the conditions for the number of boxes. If a box may not be able to insert to anywhere, that individual is deleted and an individual is newly generated.
From a constrained GA in above, our proposal is able to meet the conditions for our optimization problem.
5. Experiments
In this section, we validate the effectiveness of a constrained GA for optimization of a production line. The parameters for a constrained GA are shown in Table 3. The fitness function is as the Eq. (1).
Fig. 4 illustrates the changes in the fitness value of the best individual. Positions for racks and assembly boxes are randomly determined in the first generation; therefore, the maximum time for picking up in the first generation is about 70.9 second and the minimum is about 65.3 second.
| Case 1 | Case 2 | |
|---|---|---|
| Num. of Individuals | 4000 | |
| Num. of Generations | 50000 | |
| Prob. of Crossover(Racks) | 0.08 | 0.07 |
| Prob. of Mutation(Racks) | 0.02 | 0.025 |
| Prob. of Crossover(Boxes) | 0.08 | 0.07 |
| Prob. of Mutation(Boxes) | 0.02 | 0.025 |
| Num. of Evaluation Cars | 500 | |
The parameters for a constrained GA.
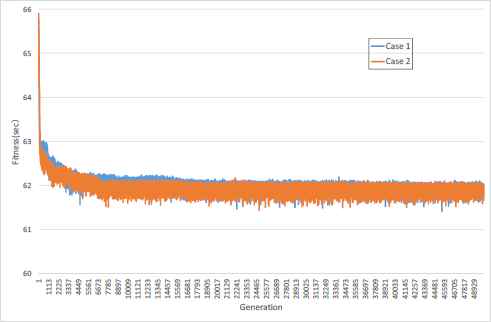
Optimization results. “Blue line” shows “Case 1” and “Orange line” shows “Case 2” in Table 3.
In contrast with the first generation, the time for picking up assemblies from the optimized positions in last generation is about 61.7 second from Fig. 4. For this, our proposal achieved to reduce about 10 seconds per a car compared with random positioning.
6. Conclusions
We propose to optimize a production line of cars manufacturing plant by GA in this paper. The difficulties of our aim are that parameters of optimization in our problem are dependent on each other because the number of racks to put assembly boxes and that boxes is predetermined. Consequently, we are not able to apply conventional GA to optimization. For this, we apply a “constrained GA” to optimization for positions of racks and boxes in a production line.
From the results of experiment, our proposal achieved to reduce about 10 seconds per a car compared with random positioning.
References
Cite this article
TY - JOUR AU - Keiji Kamei AU - Takafumi Arai PY - 2018 DA - 2018/09/30 TI - Optimization for Line of Cars Manufacturing Plant using Constrained Genetic Algorithm JO - Journal of Robotics, Networking and Artificial Life SP - 131 EP - 134 VL - 5 IS - 2 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.2018.5.2.13 DO - 10.2991/jrnal.2018.5.2.13 ID - Kamei2018 ER -
