Utilizing the Similarity Meaning of Label in Class Cohesion Calculation
- DOI
- 10.2991/jrnal.k.201215.013How to use a DOI?
- Keywords
- Software engineering; software quality; design quality; cohesion metric; D3C2 metric
- Abstract
The cohesion is one of the design quality indicators in software engineering. The measurement of the value of cohesion is done by looking at the correlation between attributes and methods that are in a class. In Direct Distance Design Class Cohesion (D3C2) metrics, attributes, and methods are assumed to have a good correlation if they have a similar type. But, the similarity of type parameters and attributes do not always indicate that these attributes are managed (correlated) in the method. This study is trying to gain information that can enhance the degree of certainty of a correlation between the methods and attributes. Relatedness between them has been seen from closeness the meaning of the name tag attribute, method, and parameters. The experimental results declared an increase in the value of cohesion produced in line with the similarity of meaning.
- Copyright
- © 2020 The Authors. Published by Atlantis Press B.V.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Software engineering is a discipline that has a purpose to provide a way or method to build a qualified software system [1]. Each development phase must be carried out in an orderly and synchronous manner with each other. So that one phase and the other is traceable. The previous phase will give effect to the next phase. Maintaining the quality of the software not only focuses on one specific phase, but it should be maintained at every phase so that the resulting qualified software. The design phase is the second phase after requirement analysis is finished. The design phase aims to produce a description of the structure of the software, data models, data structures, interfaces between system components, and the algorithms used [1]. The quality of design affects the final result of the software. There is a mechanism to assess the quality of software design artifact. Metric is one that can be used to quantified the quality. Cohesion is one of the indicators for assessing the quality of a result of design [2–4].
Cohesion is a level of relatedness between elements within a component [2]. The higher value of cohesion means the relatedness between elements is high. The higher the value of cohesion in a component, then the better the design [5,6]. For example, in the development of software with an object-oriented approach, there is a class which is a component, an element that is in the class include the attributes and methods [2]. The high cohesion means the relation between attribute and method, attribute and attribute, and method and method is high. If it is high then the class is full of relations and compact. The high cohesion can increase the maintainability of classes that exist in the system. The changes in one class will not affect the other class. The maintenance of the system can be easily and focus on the problem [6].
The process of calculating the value of the cohesion of a class will be very useful in maintaining the quality of the design [2,3]. The measurement of cohesion at the design phase has a purpose to provide information about the quality of the design as soon as possible. Knowing it can save the cost and effort of developers to perform maintenance.
One metric that can be used to measure the value of cohesion that considers the interrelationships between attributes and methods are the Distance Design-based Direct Class Cohesion and then called D3C2 [2]. D3C2 metric considering the relatedness between elements by seeing the similarity of parameter type in the method of class and the unique attribute type. A method assumed has high relatedness if the parameter type of method is the same as the attribute type of the class. At the design phase, the source code of the system has not been defined yet. The certainty that an attribute is manipulated by a method is low. This condition raises the thought that similarity parameter types and attribute types do not always indicate that an attribute associated with the method. On the other hand, some attributes are manipulated by a method which does not have the same parameter types as attribute types.
This study tries to explore the information that can enhance the degree of certainty of the relationship between methods and attributes of the class. Based on the theory, the maintainability of software is affected by the naming of a variable (attributes and method) [1]. The naming of a label of attributes and methods in the inner class must be informative. the naming of attributes and methods must describe the purpose of why they must be defined. This research is assumed that the naming of attributes and methods is done informatively. One of the purposes of this research is to find the correlation between attributes and methods not only looked at the similarity of type but also the name. The similarity of names is not only seen from the similarities of syntax but also views of the similarity of meaning (semantics). Then, the experimental results applied to the D3C2 metrics to calculate the value of cohesion in a real case. The result using D3C2 cohesion metrics with the semantic approach is used to compare with the previous approach.
2. COHESION METRIC
Cohesion metric is a measure of the quality attributes of the object-oriented program and refers to the level where class members are related. Measurement cohesion class to get the value of the quality of software products and as a guide for the restructuring of the bad class design program. Some metrics class cohesion has a purpose as literature, and some of these metrics are used for validation purposes based on mathematical measurement of class cohesion [7].
Direct Attribute Type (DAT) is a matrix used to map the relatedness between method and attribute [2]. DAT is created as the basis for the calculation of the D3C2 metric. DAT matrix is prepared by comparing the method’s type and the attribute’s type. The example of the DAT matrix from class ColourSettings (Figure 1) is described in Table 1. Based on the DAT matrix, the following four metrics have to calculate before D3C2 will calculate [2].

Class ColourSettings.
| long | ColourEntry | ColourEntry | ColourEntry | ColourEntry | Picture | |
|---|---|---|---|---|---|---|
| ColourSettings | 0 | 0 | 0 | 0 | 0 | 1 |
| restore | 0 | 0 | 0 | 0 | 0 | 0 |
| toString | 0 | 1 | 1 | 1 | 1 | 0 |
| toString | 0 | 0 | 0 | 0 | 0 | 0 |
DAT matrix using previous research
2.1. Method–Method through Attributes Cohesion
Method–Method Attributes through Cohesion (MMAC) is a metric to calculate an average value of cohesion of all pairs of methods. MMAC is formally written as follows:
2.2. Attribute–Attribute Cohesion
Attribute–Attribute Cohesion (AAC) is a metric to calculate the average value of cohesion of pair of attributes. AAC is formally written as follows:
2.3. Attribute–Method Cohesion
Attribute–Method Cohesion (AMC) is a metric to calculate an average value of cohesion based on the interaction of attributes and methods. AMC is formally written as follows:
2.4. Distance Design-based Direct Class Cohesion
This process can’t be defined if a class does not have class methods and attributes. D3C2 metrics used to calculate the final summation of the result of MMAC, AAC, and AMC. D3C2 is formulated as follows:
3. SEMANTIC SIMILARITY
Dictionary or repository of words that can be used to assist in the identification of words that mean the same thing has been developed and used in several studies [8,9]. A WordNet is a dictionary that has been prepared based on the relation of synonyms, antonyms, hyponyms, and hypernyms, meronyms, troponin, and entailment relationships [10]. Wu and Palmer [11] formulate a way of comparing the meanings of the two words by considering the proximity of the relations in the word’s dictionary.
In a study conducted by Dijkman et al. [12], Dijkman defines a formula for calculating the similarity between the two labels or sentence by considering the similarity of meanings (synonyms). Semantic similarity can be calculated using the following formula:
4. METHODOLOGY
Figure 2 shows the flow of the automatic calculation system. The first step in this research is receiving the XML files. Those files are generated from design tools named Visual Paradigm for UML. The calculation of the value of cohesion is performed by using prototype software that is developed using Java language. The results will be stored in storage, which will then be analyzed.

The process of calculation.
In D3C2 metric calculation process, it is necessary first to calculate metrics MMAC, ACC, and AMC. In previous studies, the DAT matrix is formed by giving the value 1 for the pair method and attribute which has the same type. In this study, the DAT matrix is prepared by comparing the method of the semantic similarity of the name of the method and attributes besides considering the similarity of type. If there is no type recognized, then the semantic similarity is considered. The system has to be able to split the words inner both names to make a comparison semantically between words from the label name of method and attribute.
After splitting the name of methods and attributes, then every name label (consist of words after splitting) is comparing semantically using Equation (5) and a threshold of 0.5. WordNet will enrich Equation (5) to calculate the similarity of words. If the score is above the threshold, then it is considered as similar semantically. For an example of the calculation is, there are two label name “getBirthDate” and “BirthDay”. Syntactically, it is different, but if we look at the context meaning it is very close. The implementation of the calculation using Equation (5) to the example of the label is explained as follows. First “getBirthDate” is split to “get”, “Birth” and “Date” (w1). And, “BirthDate” split into “Birth” and “Date” (w2). |w1 ∩ w2| = 1, because there is a couple of words that exactly similar is “Birth”. (|s(w1, w2)| + |s(w2, w1)|) is looking at the rest of the words that have synonym similarity from w1 to w2 and w2 to w1. Between the rest of the words in w1 to w2 there is only one couple synonym, the word is “Date” and “Day”. “Date” and “Day” are calculated using WordNet has a score of synonymity of 0.92. So, (|s(w1, w2)| + |s(w2, w1)|) = 1, represent the number of synonym couple between w1 and w2. If all of this is put together using Equation (5) then can be described as follow (wi = 1 and ws = 0.75).
Because the result of the calculation is 0.55 (above threshold 0.5), then “getBirthDate” and “BirthDay” are considered semantically similar. And, this result will be represented to the purposed DAT matrix by giving a value of 1 into the purposed DAT matrix. The example of the semantic DAT matrix is described in Table 2. After the DAT matrix is completed, then the calculation of the D3C2 metric can be done.
| (serialVersion UID) long | (foreground) ColourEntry | (background) ColourEntry | (transparent) ColourEntry | (pictureBackground) ColourEntry | (picture) Picture | |
|---|---|---|---|---|---|---|
| ColourSettings | 0 | 0 | 0 | 0 | 1 | 1 |
| restore | 0 | 1 | 0 | 0 | 0 | 0 |
| toString | 0 | 1 | 1 | 1 | 1 | 0 |
| toString | 0 | 0 | 0 | 0 | 0 | 0 |
Proposed DAT matrix (Semantic DAT)
5. RESULT AND DISCUSSION
It needs several things to test the prototype. The input is the class diagram that is exported as an XML file by using Visual Paradigm. The data selected for this testing is the source code of the application jDraw version 1.1.5 available on the website www.sourceforge.net.
5.1. Result
The result of the calculation will be compared with the manual observation to get the conformance between the approach. Calculating the conformance between approach is using the Kappa coefficient. The Kappa coefficient between the previous approach and the semantic approach is descript in Tables 3 and 4.
| KOHENS KAPPA | |||
|---|---|---|---|
| Observer | |||
| System | Y | N | Total |
| Y | 49 | 343 | 392 |
| N | 123 | 1401 | 1524 |
| Total | 172 | 1744 | 1916 |
| Po | 0.756785 | ||
| Pc | 0.7423695 | ||
| Kappa | 0.055954 | Slight agreement | |
Kappa of the previous approach
| KOHENS KAPPA | |||
|---|---|---|---|
| Observer | |||
| System | Y | N | Total |
| Y | 54 | 82 | 136 |
| N | 118 | 1662 | 1780 |
| Total | 172 | 1744 | 1916 |
| Po | 0.895616 | ||
| Pc | 0.851992 | ||
| Kappa | 0.29474 | Fair agreement | |
Kappa of semantic approach
The result shows that there is an increment of value of Kappa from 0.055954 to 0.29474 between the previous and semantic approaches. Based on the level of Kappa, it is also increasing from slight agreement to fair agreement.
5.2. Discussion
Examples of cases of jDraw are a class named ColourSettings, as illustrated in Figure 1. Table 5 shows the result of calculation D3C2 using the previous approach and the semantic approach.
| Previous approach | Semantic approach | ||||||
|---|---|---|---|---|---|---|---|
| MMAC | ACC | AMC | D3C2 | MMAC | ACC | AMC | D3C2 |
| 0.0 | 0.1 | 0.21 | 0.14 | 0.05 | 0.11 | 0.29 | 0.2 |
Comparison D3C2 value
D3C2 metric final results showed an increase in the value of 0.144 into 0.2 (0.056 difference). In a previous study, attributes pictureBackground has no connection with the method ColourSettings (constructor), due to ColourEntry data types not contained in the type parameter or returns the data type of a method ColourSettings. pictureBackground has close meaning with the method ColourSettings and parameter aPicture using the semantic approach. In the source code of method ColourSettings, the method manipulates attributes pictureBackground. It shows that there is a connection between the pictureBackground attribute with a constructor method ColourSettings. Figure 3 shows the presence of pictureBackgound in the body of the ColourSettings method.
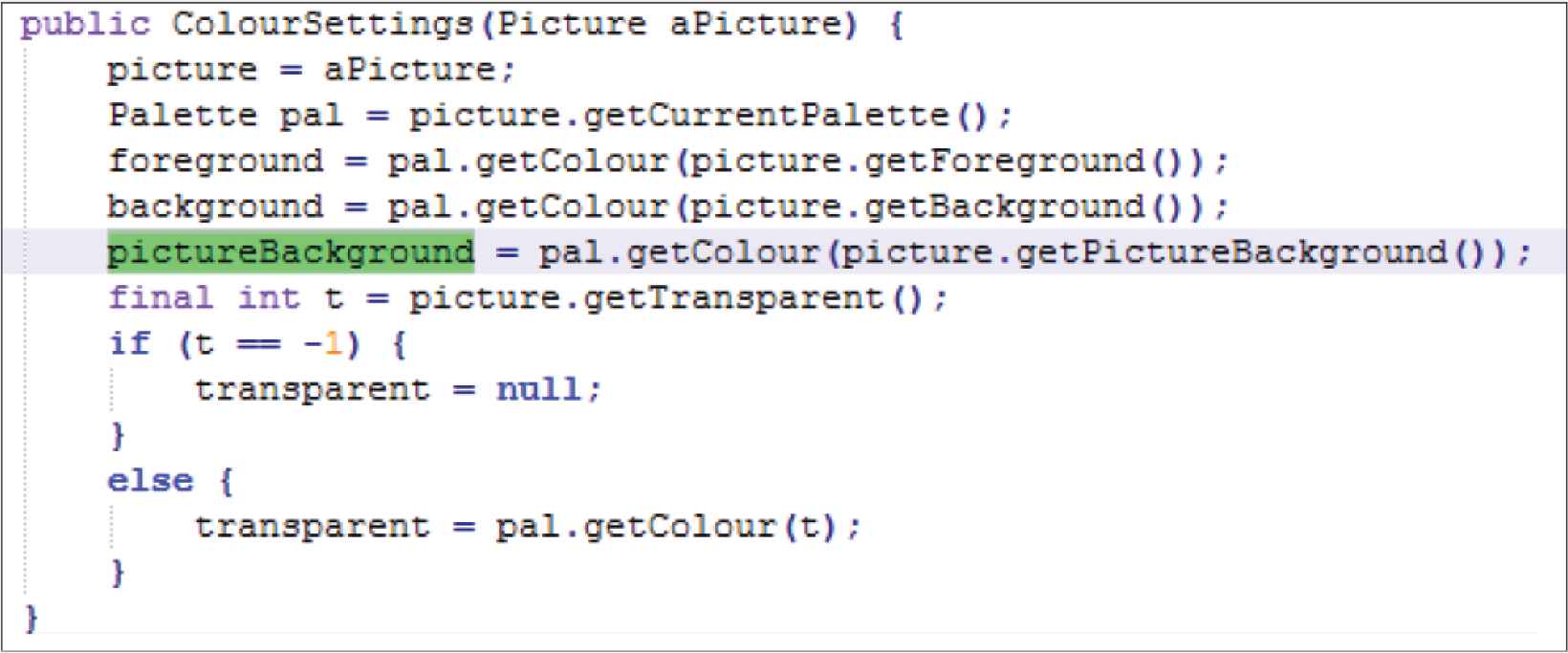
The code of method ColourSettings.
6. CONCLUSION
Cohesion calculation at the design phase has challenges because of the lack of information is provided by the design artifact, such as class diagram. The application of the semantic approach in calculating D3C2 metrics can increase the conformance of the calculation results. In the future, it is essential if there is any additional information considered other than class diagrams.
The process flow in the method described in the flow diagram or pseudo code in the design phase is worth considering.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
AUTHORS INTRODUCTION
Bayu Priyambadha
 He has received his Bachelor of Computer from 10 November Institute of Technology Surabaya. He also has got a Master of Computer from 10 November Institute of Technology Surabaya. He is a member of the Software Engineering Research Group (SERG) in the Faculty of Computer Science, Brawijaya University, Indonesia. He is currently a doctoral student at the University of Miyazaki, Japan. His current research interest is Software Engineering, Software Design, Software Quality, and Software Maintenance.
He has received his Bachelor of Computer from 10 November Institute of Technology Surabaya. He also has got a Master of Computer from 10 November Institute of Technology Surabaya. He is a member of the Software Engineering Research Group (SERG) in the Faculty of Computer Science, Brawijaya University, Indonesia. He is currently a doctoral student at the University of Miyazaki, Japan. His current research interest is Software Engineering, Software Design, Software Quality, and Software Maintenance.
Tetsuro Katayama
 He received a PhD degree in engineering from Kyushu University, Fukuoka, Japan in 1996. From 1996 to 2000 he has been a Research Associate at the Graduate School of Information Science, Nara Institute of Science and Technology, Japan. Since 2000 he has been an Associate Professor at Faculty of Engineering, Miyazaki University, Japan. He is currently a Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include software testing and quality. He is a member of the IPSJ, IEICE, and JSSST.
He received a PhD degree in engineering from Kyushu University, Fukuoka, Japan in 1996. From 1996 to 2000 he has been a Research Associate at the Graduate School of Information Science, Nara Institute of Science and Technology, Japan. Since 2000 he has been an Associate Professor at Faculty of Engineering, Miyazaki University, Japan. He is currently a Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include software testing and quality. He is a member of the IPSJ, IEICE, and JSSST.
Yoshihiro Kita
 He received a PhD degree in systems engineering from the University of Miyazaki, Japan, in 2011. He is currently an Associate Professor with the Faculty of Information Systems, University of Nagasaki, Japan. His research interests include software testing and biometrics authentication.
He received a PhD degree in systems engineering from the University of Miyazaki, Japan, in 2011. He is currently an Associate Professor with the Faculty of Information Systems, University of Nagasaki, Japan. His research interests include software testing and biometrics authentication.
Hisaaki Yamaba
 He received the B.S. and M.S. degrees in chemical engineering from the Tokyo Institute of Technology, Japan, in 1988 and 1990, respectively, and the PhD degree in systems engineering from the University of Miyazaki, Japan, in 2011. He is currently an Assistant Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include network security and user authentication. He is a member of SICE and SCEJ.
He received the B.S. and M.S. degrees in chemical engineering from the Tokyo Institute of Technology, Japan, in 1988 and 1990, respectively, and the PhD degree in systems engineering from the University of Miyazaki, Japan, in 2011. He is currently an Assistant Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include network security and user authentication. He is a member of SICE and SCEJ.
Kentaro Aburada
 He received the B.S., M.S., and PhD degrees in computer science and system engineering from the University of Miyazaki, Japan, in 2003, 2005, and 2009, respectively. He is currently an Associate Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include computer networks and security. He is a member of IPSJ and IEICE.
He received the B.S., M.S., and PhD degrees in computer science and system engineering from the University of Miyazaki, Japan, in 2003, 2005, and 2009, respectively. He is currently an Associate Professor with the Faculty of Engineering, University of Miyazaki, Japan. His research interests include computer networks and security. He is a member of IPSJ and IEICE.
Naonobu Okazaki
 He received his B.S., M.S., and PhD degrees in electrical and communication engineering from Tohoku University, Japan, in 1986, 1988 and 1992, respectively. He joined the Information Technology Research and Development Center, Mitsubishi Electric Corporation in 1991. He is currently a Professor with the Faculty of Engineering, University of Miyazaki since 2002. His research interests include mobile network and network security. He is a member of IPSJ, IEICE and IEEE.
He received his B.S., M.S., and PhD degrees in electrical and communication engineering from Tohoku University, Japan, in 1986, 1988 and 1992, respectively. He joined the Information Technology Research and Development Center, Mitsubishi Electric Corporation in 1991. He is currently a Professor with the Faculty of Engineering, University of Miyazaki since 2002. His research interests include mobile network and network security. He is a member of IPSJ, IEICE and IEEE.
REFERENCES
Cite this article
TY - JOUR AU - Bayu Priyambadha AU - Tetsuro Katayama AU - Yoshihiro Kita AU - Hisaaki Yamaba AU - Kentaro Aburada AU - Nanoubu Okazaki PY - 2020 DA - 2020/12/31 TI - Utilizing the Similarity Meaning of Label in Class Cohesion Calculation JO - Journal of Robotics, Networking and Artificial Life SP - 270 EP - 274 VL - 7 IS - 4 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.201215.013 DO - 10.2991/jrnal.k.201215.013 ID - Priyambadha2020 ER -
