Digital Hardware Spiking Neuronal Network with STDP for Real-time Pattern Recognition
- DOI
- 10.2991/jrnal.k.200528.010How to use a DOI?
- Keywords
- SNN; STDP; DSSN; FPGA; ethernet
- Abstract
By mimicking or being inspired by the nervous system, neuromorphic systems are designed to realize robust and power-efficient information processing by highly parallel architecture. Spike Timing Dependent Plasticity (STDP) is a common learning method for Spiking Neural Networks (SNNs). Here, we present a real-time SNN with STDP implementation on Field Programmable Gate Array (FPGA) using digital spiking silicon neuron model. Equipped with Ethernet Interface, FPGA allows online configuration as well as real-time processing data input and output. We show that this hardware implementation can achieve real-time pattern recognition tasks and allows the connection between multi-SNNs to extend the scale of networks.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
Neuromorphic systems are designed by mimicking or being inspired by the nervous system, which aims to process information in robust, autonomous, and power-efficient manner. There are three common methods to realize them, which are software [1], analog hardware [2,3] and digital hardware [4–6]. Compared to analog circuits, digital implementations generally consume higher power but are more scalable and tunable and less sensitive to noise and fabrication mismatch. Compared to software implementation, digital hardware works in real-time.
Spiking Neuronal Network (SNN) is inspired by information processing in the nervous system and can reproduce its electrophysiological activities by implementation on neuromorphic circuits.
The SNNs are modeled by focusing on asynchronous spiking dynamics in the neuronal cells and their transmission via the synapses. Their application includes bio-inspired information processing such as pattern recognition [7,8] and associative memory [9] as well as neuro-prosthetic devices [10–12].
Digital SNNs are expected to realize a very large-scale network comparable to the human brain in the future exploiting the scalability of digital circuits. In the last years, several very large-scale SNNs with one million neurons were developed [13].
Spike Timing Dependent Plasticity (STDP) is a well-known rule for updating the synaptic efficacy in SNNs, which uses only local information. There are many evidences found for STDP process in the synapses [14,15] in biological experiments.
In this paper, we report an implementation of digital SNN with online STDP learning on Field Programmable Gate Array (FPGA). The model and implementation of our SNN are explained in Sections 2 and 3, respectively. Then results and conclusion follows.
2. ARCHITECTURE OF THE NETWORK MODEL
2.1. DSSN Model
Choice of neuronal models needs considering the balance between the reproducibility of neuronal activity and computational efficiency. Integrate-and-fire-based models are able to be implemented by compact hardware, but they lack reproducibility of complex neuronal dynamics. Ionic-conductance models have a high ability to reproduce neuronal activities, but it requires massive computational resources. The Digital Spiking Silicon Neuron (DSSN) model is a qualitative neural model [16], which was designed for efficient implementation in digital circuits. The simplest version of DSSN model supports the Class I and II cells in Hodgkin’s Classification [17]. The differential equations of DSSN model are as follows.
Here v represents the membrane potential, n is a variable that reflects the activities of hyperpolarizing ionic channels. axy, bxy, and cxy (x = f, g and y = n, p) are parameters. Istm represents the input stimulus and the parameter I0 is a bias constant. The only nonlinearity in the DSSN model is a quadratic function. Therefore, numerically solving this model using Euler’s method requires just one multiplication operation per step if the parameters are carefully selected [9,18]. Due to the high resource requirements of digital circuits for multiplication operations, the DSSN model is suitable for digital SNN circuit.
2.2. Synaptic Model
Post-synaptic Current (PSC) is a type of current inserted into the post-synaptic cell that induces temporal change in its membrane potential. The PSCs generated by pulse-stimulated chemical synapses are able to be modeled by the alpha function with double-exponential generalization [19]. In our network model, the PSP model was simplified to one exponential function as follows.
2.3. STDP Algorithm and Architecture
Synaptic plasticity is a basis for learning in the nervous system. The synaptic efficacy is updated in response to the activities of pre- and post-synaptic neurons.
The STDP is a rule for synaptic plasticity that adjusts the strength of synaptic connections (w) based on the relative timing of the spikes in a pre- and post-synaptic neurons. Recently it has been shown how STDP rule play a key role by detecting repeating patterns and generating selective response to them [20].
The STDP rule is a most common form of learning rules used in SNNs. Here is the standard exponential STDP equations.
3. IMPLEMENTATION
The overall architecture of our SNN is shown in Figure 1. The DSSN, STDP, and PSC blocks were implemented on a FPGA board. In this development platform, three post-synaptic neurons are each connected with 500 input afferent neurons for detecting one certain repeating pattern. All the circuits were described using Very High Speed Hardware Description Language (VHDL). Stimulus spike trains were generated by Brian2 on PC and sent to FPGA via Ethernet connection which are explained in Subsection 3.4.
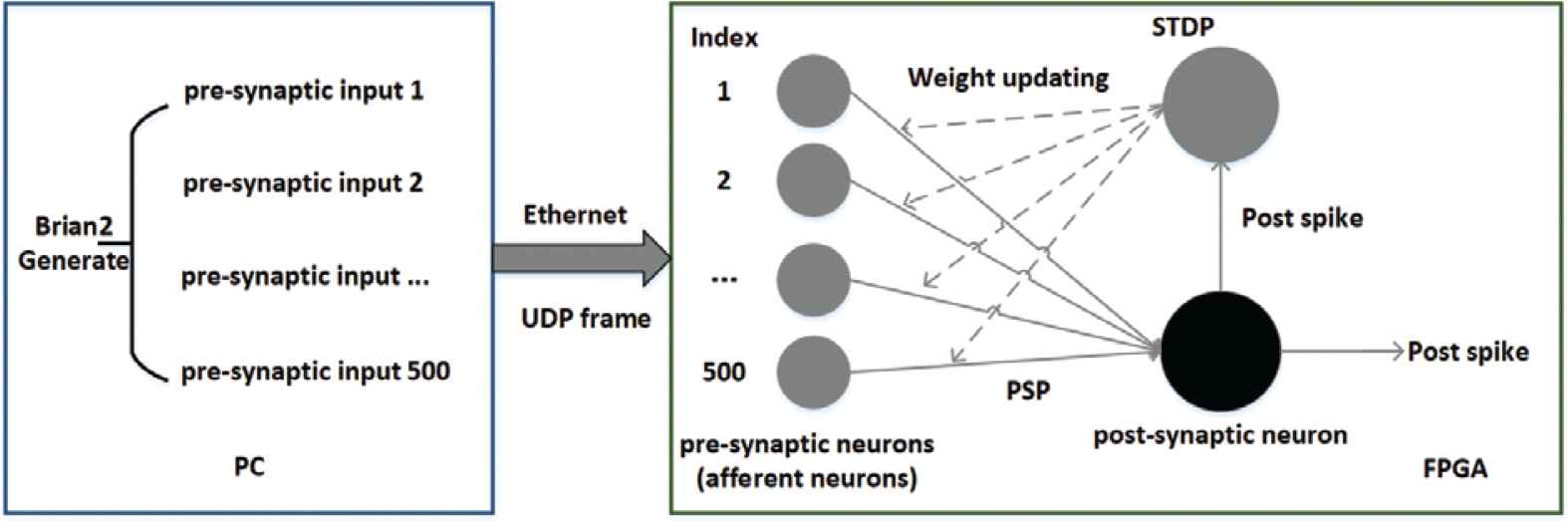
Overall architecture of STDP learning.
3.1. Implementation of DSSN
Euler’s method is used to solve the differential equation of the DSSN model with the timestep of 0.1 ms. The solver circuit uses Time Division Multiplexing (TDM) and pipelined architecture Each DSSN model cost 0.19% Look-Up-Tables (LUT) in Xilinx XC7K325T chip [18].
3.2. Implementation of PSC
As introduced in Subsection 2.2, we use a simplified exponential decay to approximate the PSCs. The connection between a post-synaptic neuron and the 500 pre-synaptic neurons was calculated efficiently by using TDM and two-stage pipeline as in the DSSN solver circuit. By using a single multiplier and a single adder, 500 sets of PSC operations are completed in 1000 clock cycles with a frequency of 100 MHz. If the system clock is higher than 100 MHz, the time step of the summation of PSCs is within 0.1 ms.
3.3. Implementation of STDP Learning
Based on the STDP rule, each pre-synaptic (post-synaptic) spike, induces an LTD (LTP) where the synaptic weight is updated according to Equation (7). An example waveform of STDP learning process is shown in Figure 2, where the solid and dotted red curve represent the pre- and post-synaptic spikes, as well as the black curve is the strength of synaptic connection. In order to simulate 500 afferent inputs, 500 clock cycles were consumed. Calculation of exponential function and update of synaptic efficacy are executed by TDM.

Waveform of STDP method implementation.
3.4. Ethernet on FPGA
Ethernet is a computer networking technology commonly used in Local Area Networks (LAN). Devices equipped with Ethernet interfaces are connectable to LAN as well as the internet by supporting common communication protocol, for instance, TCP/IP and User Datagram Protocol (UDP). When implementing neuron networks on FPGAs, the transmission of spikes has always been an issue when the neuronal network becomes large.
By implementing Ethernet interface and a full hardware protocol stack including IP, UDP and Address Resolution Protocols (ARP), our SNN on FPGA is capable of receiving input spike patterns from a PC via Ethernet connection and sending report frame back to the PC for monitoring the SNN working status.
The configuration and parameter setting are also possible by the Ethernet connection, which contribute to take full advantage of the flexibility and portability of FPGAs.
4. PATTERN RECOGNITION
Spatiotemporal spike pattern recognition tasks proposed by Masquelier et al. [21] were performed on our network. In these tasks, the stimulus patterns were generated by superimposing a spatiotemporal spike pattern at many time points on a background random spike pattern (see Figure 3a). The former spike patterns (ones to be detected) were generated by PoissonGroup Function in Brian2 (a Python library) on PCs. The background random spike patterns were generated using the same library. The stimulus patterns were stored in files and sent from the PC to the FPGA via the Ethernet connection. In the afferent input spike train, spike patterns to be detected appears repeatedly. Given such input, STDP learning eventually makes post-synaptic neurons generate a spike in response to one of the spike patterns to be detected (see Figure 3b). Rate of successful recognition versus number of post-synaptic neurons is shown in Figure 4. Here, the post-synaptic neurons have different initial weight distributions each other. When the network comprises three post-synaptic neurons or more, the success rate was 100%. Our circuit performed this task in real-time with FPGA’s system clock of 100 MHz.

(a) An example of afferent input data and (b) waveform of a postsynaptic neuron’s membrane potential that learned to generate a spike in response to an input spike pattern [red dots in (a)].
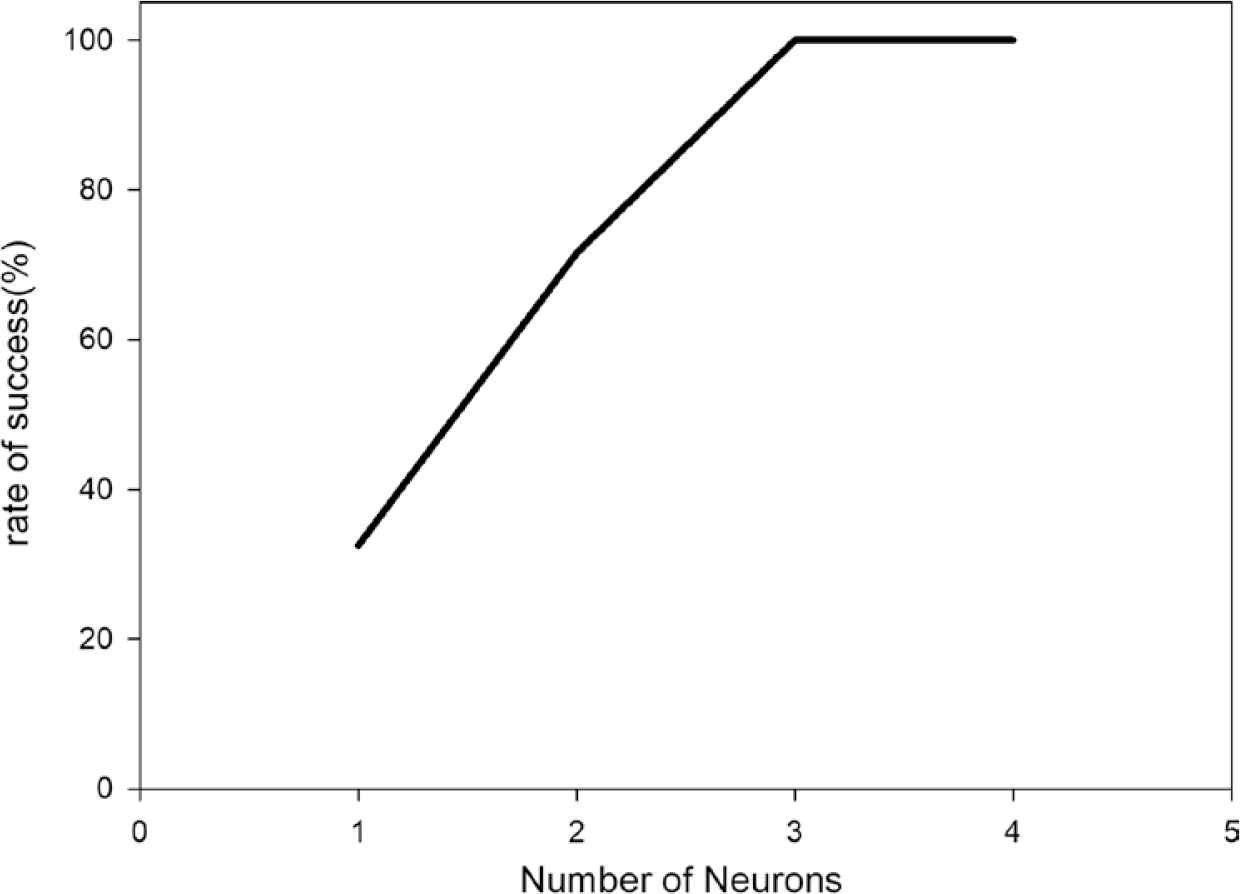
Three post-synaptic neurons lead to 100% of learning success rate.
5. CONCLUSION
In this paper, a SNN on an FPGA with STDP learning capability were reported. The stimulus spikes were transmitted to the FPGA chip in real-time via Ethernet connection. Experimental results support that our SNN has real-time spatiotemporal spike pattern recognition capability.
In this work, the input patterns were generated on a PC. Generating them in real-time with another SNN is a future work. By increasing the number of the post-synaptic neurons, multi-repeating-pattern detection at the same time will be realized in our circuit in the future. Since the number of on-chip memories used to store the strength of synaptic connections limits the size of the network on the FPGA chip, it is also planned to develop an FPGA–FPGA connection bus to extend the scalability of FPGA-based SNNs. From the perspective of real-time and power consumption, the SNN platform has higher scalability than software simulation.
CONFLICTS OF INTEREST
The authors declare they have no conflicts of interest.
ACKNOWLEDGMENT
This work was supported by JSPS KAKENHI Grant Number 15KK0003.
AUTHORS INTRODUCTION
Mr. Yang Xia
 He is a PhD student in Kohno laboratory at University of Tokyo. He got his bachelor and master degree in Beijing Insistute of Techonology. His research interests are Silicon Neuronal Network, communication protocol and FPGA devices.
He is a PhD student in Kohno laboratory at University of Tokyo. He got his bachelor and master degree in Beijing Insistute of Techonology. His research interests are Silicon Neuronal Network, communication protocol and FPGA devices.
Dr. Timothée Levi
 He received the PhD degree in Electronics at The University of Bordeaux, France, in 2007. He is an Associate Professor at IMS lab. of The University of Bordeaux, since 2009, and a Project Associate Professor at The University of Tokyo since 2017. His research interest deals with neuromorphic engineering for bio-hybrid experiments.
He received the PhD degree in Electronics at The University of Bordeaux, France, in 2007. He is an Associate Professor at IMS lab. of The University of Bordeaux, since 2009, and a Project Associate Professor at The University of Tokyo since 2017. His research interest deals with neuromorphic engineering for bio-hybrid experiments.
Dr. Takashi Kohno
 He has been with the Institute of Industrial Science at the University of Tokyo, Japan since 2006, where he is currently a Professor. He received the B.E. degree in medicine in 1996 and the PhD degree in Mathematical Engineering in 2002 from the University of Tokyo, Japan.
He has been with the Institute of Industrial Science at the University of Tokyo, Japan since 2006, where he is currently a Professor. He received the B.E. degree in medicine in 1996 and the PhD degree in Mathematical Engineering in 2002 from the University of Tokyo, Japan.
REFERENCES
Cite this article
TY - JOUR AU - Yang Xia AU - Timothée Levi AU - Takashi Kohno PY - 2020 DA - 2020/06/02 TI - Digital Hardware Spiking Neuronal Network with STDP for Real-time Pattern Recognition JO - Journal of Robotics, Networking and Artificial Life SP - 121 EP - 124 VL - 7 IS - 2 SN - 2352-6386 UR - https://doi.org/10.2991/jrnal.k.200528.010 DO - 10.2991/jrnal.k.200528.010 ID - Xia2020 ER -
