Journal of Nonlinear Mathematical Physics

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 27, Issue 2, January 2020, Pages 243 - 266

Canonical spectral coordinates for the Calogero-Moser space associated with the cyclic quiver

Authors
Tamás Görbe
School of Mathematics, University of Leeds Leeds, LS2 9JT, UK,T.Gorbe@leeds.ac.uk
Ádám Gyenge
Mathematical Institute, University of Oxford Andrew Wiles Building, Radcliffe Observatory Quarter Woodstock Road OX2 6GG, Oxford, UK,Adam.Gyenge@maths.ox.ac.uk
Received 3 February 2019, Accepted 29 August 2019, Available Online 27 January 2020.
DOI
10.1080/14029251.2020.1700634How to use a DOI?
Keywords
Calogero-Moser; cyclic quiver; Darboux coordinates; canonical spectral coordinates; Sklyanin’s formula
Abstract

Sklyanin’s formula provides a set of canonical spectral coordinates on the standard Calogero-Moser space associated with the quiver consisting of a vertex and a loop. We generalize this result to Calogero-Moser spaces attached to cyclic quivers by constructing rational functions that relate spectral coordinates to conjugate variables. These canonical coordinates turn out to be well-defined on the corresponding simple singularity of type A, and the rational functions we construct define interpolating polynomials between them.

Copyright
© 2020 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. Introduction

The n-th Calogero-Moser space 𝒞n can be viewed as the completed phase space of the n-particle rational Calogero-Moser (CM) system [1,11, 19]. This system describes n interacting particles with positions q =(q1,...,qn) and momenta p =(p1,...,pn) evolving in time according to Hamilton’s equations

dqjdt=∂H∂pj,dpjdt=−∂H∂qj,   j=1,…,n(1.1)
given by the Hamiltonian
H(p,q)=∑j=1npj22+∑1≤j<k≤nγ(qj−qk)2.(1.2)

Here γ is a parameter that controls the strength of particle interaction, which itself is defined via a pair-potential that is inversely proportional to the square of the difference of particle-positions. This system has many conserved quantities, i.e. functions F such that {H,F} = 0, that can be obtained as spectral invariants of a matrix-valued function of q and p, that is the Lax matrix of the system. Moreover, the eigenvalues of the Lax matrix of the CM system form a complete set of Poisson commuting first integrals, hence the CM system is Liouville integrable [11]. This encourages the investigation of the spectrum of the Lax matrix. These eigenvalues provide partial parametrisation of the CM space on the dense open subset where the Lax matrix is diagonalisable. A natural question is to find a set of conjugate variables in order to obtain a full parametrisation compatible with the symplectic structure ∑j=1ndpj∧dqj. Sklyanin formulated a conjectural expression for conjugate variables in [16]. Utilizing the bi-Hamiltonian structure of the classical CM system, this conjecture was proved in [5]. Another proof of Sklyanin’s formula was given in [8] using Hamiltonian reduction [9].

Canonical spectral coordinates are central to the algebro-geometric approach to integrable systems [15]. In general, when the Lax matrix of a system depends on a spectral parameter z, canonical coordinates are given by the location of the poles of a (suitably normalized) eigenvector of the Lax matrix L(z). Equivalently, the coordinates are given by the locations on the spectral curve det(λ1 − L(z)) of the points corresponding to the zeros of a specific polynomial. However, this method cannot be applied directly to the rational CM-system, because all poles of the eigenvector are located above z = ∞, hence the z coordinates of these poles do not provide conjugate variables to the eigenvalues of the specialized (spectral parameter independent) Lax matrix L(∞). A formula conjectured by Sklyanin [16] resolves exactly this problem. Instead of the coordinate z, some other function associated with the dynamical variables should be used to express the conjugate variables.

The classical CM space 𝒞n is also a particular example of a quiver variety [7, 12]. Namely, it is associated with the quiver consisting of only one vertex with a loop attached to it. More general Calogero-Moser spaces associated with other quivers can be constructed in a similar manner. In this work, we investigate the CM space associated with the cyclic quiver as introduced in [3]. For short, we will call it the equivariant Calogero-Moser space since it can be thought of as the completed phase space of the equivariant n-particle rational Calogero-Moser system under the action of the cyclic group of order m. We will denote it by 𝒞nm. Our main observation is that, similarly to the non-equivariant case 𝒞n=𝒞n1, an explicit formula for the conjugate variables on 𝒞nm can be given.

One can go even further by allowing the particles to have spin, i.e. internal degrees of freedom. The corresponding space will be denoted by s𝒞nm, where we suppressed the dimension of the space of internal states. We extend our results to this case as well. Although the resulting formulas look the same as in the spinless case, the proofs differ at several points.

It was shown in [3] that on the dense open subset where the specialized Lax matrix is diagonalisable, if (λ1,...,λn) are its the eigenvalues, then there is a certain set of variables (ϕ1,...,ϕn) which are conjugate to the eigenvalues. Our first main result is the following

Theorem 1.1.

On a dense open subset of the Calogero-Moser space 𝒞nm (resp., s𝒞nm) there is a certain rational function r(z) ∈ ℂ(z) such that on a dense open subset the relationship

φi=r(λi)i=1,…,n(1.3)
between the sets of conjugate variables (ϕ1,..., ϕn) and (λ1,..., λn) holds.

Theorem 1.1 shows that although the specialized Lax matrix of the equivariant CM system does not contain a spectral parameter, the conjugate variable pairs (λi, ϕi) are still lying on an “interpolation curve” defined by the equation y = r(z). More precisely, the pair (λi, ϕi) is a well-defined point on the singular surface of type Am−1, and the interpolation curve between the points {(λi, ϕi)} is a rational curve on this singular surface.

The datum which represents a point on 𝒞nm or on s𝒞nm contains a framing, which consists of two additional vectors v and w. In the spin case the variables (λ1,...,λn) and (ϕ1,..., ϕn) together with the coordinates of the vectors v and w form a complete set of canonical coordinates, whereas in the spinless case the coordinates of v and w can always be gauged away and (λ1,...,λn, ϕ1,...,ϕn) are enough for a complete local parametrisation.

It turns out that on 𝒞n (resp., s𝒞nm) the set (ϕ1,..., ϕn) is not the only natural set of variables which is conjugate to (λ1,...,λn) [8]. The function r(z) appearing in Theorem 1.1 (including its special case for m = 1) does not depend on the framing part of the datum whereas the conjectured formula in [16], which gives another set of conjugate variables on 𝒞n in the m = 1 case, does depend on the framing. Our second result is that an analogue of Sklyanin’s formula from [16] is also valid in the equivariant case, and there is a second natural set of conjugate variables to (λ1,...,λn) which depends on the framing as well.

Theorem 1.2.

On a dense open subset of the Calogero-Moser space 𝒞nm (resp., s𝒞nm) there is a certain rational function s(z) ∈ 𝒞(z), depending also on the framing part of the datum, such that on a dense open subset the variables θ1,...,θn, defined as

θi=s(λi),  i=1,…,n(1.4)
are conjugate to λ1,...,λn, respectively.

It is known that the non-equivariant CM space 𝒞n is a deformation of the Hilbert scheme Hilbn(ℂ2) of n points on ℂ2. The framing vectors play an essential role in the stability condition of the GIT construction of Hilbn(ℂ2) as a quiver variety [13]. Hence, it seems useful to keep track of the framing vectors (or their steadiness) during a degeneration of 𝒞n into Hilbn(ℂ2). The advantage of Theorem 1.2 is that as opposed to r(z) the functions s(z) can measure such a steadiness.

Theorems 1.1 and 1.2 show that there are at least two natural sets of variables conjugate to the spectral variables (λ1,...,λn). Correspondingly, there are two natural interpolation curves on the singular surface of type Am−1.

The structure of the paper is as follows. In Section 2 we recall the recipe of separation of variables and its relation to the spectral curve with a special emphasis on the rational CM system. In Section 3 we summarize the construction and the symplectic structure on the CM space associated with the cyclic quiver. In Section 4 we prove Theorems 1.1 and 1.2 for the spinless case. In Section 5, after introducing the equivariant CM space with spin, we give the proofs of Theorems 1.1 and 1.2 for this case. In Section 6 we construct the interpolation curves on the singular surface of type Am−1.

2. Separation of variables and the spectral curve of the rational Calogero-Moser system

We briefly review the method of separation of variables (SoV) following [15]. Consider a Liouville integrable system having n degrees of freedom. This means a 2n-dimensional symplectic manifold (𝒫,ω) with n independent smooth functions H1,...,Hn on it that commute with respect to the Poisson bracket {,} induced by the symplectic form ω, i.e. {Hj,Hk} = ω(XHj,XHk)= 0, j,k = 1,...,n. A system of canonical coordinates (pj,qj), j = 1,...,n, i.e. local coordinates on the symplectic manifold satisfying

{pj,pk}={qj,qk}=0,   {pj,qk}=δj,k   j,k=1,…,n(2.1)
is called separated if there exist n relations of the form
Φj(qj,pj,H1,…,Hn)=0,   j=1,…,n.(2.2)

Such a system of variables induces an explicit decomposition of the Liouville tori into one-dimensional tori and makes several calculations about the system straightforward [15].

Suppose that the system under consideration has a Lax representation. This means that the equations of motion (1.1) can be written in the form

L˙(z)=[L(z),M(z)](2.3)
with some matrices L(z) and M(z) of size n×n, whose elements are functions on the phase space and which depend on an additional parameter z called spectral parameter. Then the functions H1,...,Hn can be expressed in terms of the coefficients t1(z),...,tn(z) of the characteristic polynomial W (Λ,z) of the matrix L(z)
W(Λ,z)=det(Λ1−L(z))=∑k=0n(−1)ktk(z)Λn−k.(2.4)

The characteristic equation

W(Λ,z)=0(2.5)
defines the eigenvalue Λ(z) of L(z) as a function on the corresponding n-sheeted Riemannian surface of the parameter z. The Baker-Akhiezer function Ω(z) is defined as the eigenvector of L(z) corresponding to the eigenvalue Λ(z), i.e. we have
L(z)Ω(z)=Λ(z)Ω(z).(2.6)

After a suitable normalization, Ω(z) becomes a meromorphic function on the Riemannian surface (2.5). Sklyanin’s formula hints that the coordinates zj of these poles play an important role. The formula is based on the observation that for many models the variables zj Poisson commute and, together with the corresponding eigenvalues Λj = Λ(zj) of L(zj), or some functions pj of zj, provide a set of separated canonical variables for the Hamiltonians H1,...,Hn. One reason for this is that since Λj = Λ(zj) is an eigenvalue of L(zj), the pair (Λj,zj) lies on the spectral curve (2.5), i.e.

W(Λj,zj)=0.(2.7)

If, furthermore, zj is a function of pj, then (2.7) provides the equations (2.2) as well.

The (complexified) rational Calogero-Moser system is a completely integrable Hamiltonian system describing a collection of n identical particles on the affine line ℂ. The phase space of the Calogero-Moser system is T *(ℂn \{all diagonals}), the configurations are n distinct unlabelled points qj ∈ ℂ with momenta pj ∈ ℂ. The Lax matrix of the system can be brought to the form [2, 10] [18, (53)]

L(z)=L+igz−1ee⊤,(2.8)
where e ∈ ℝn is the vector given by
e=(1,…,1)⊤,(2.9)
and the components of the z-independent matrix L are
Lj,k=pjδj,k+ig(qj−qk)−1(1−δj,k),   j,k=1,…,n.(2.10)

As it was observed in [18, Section 5.2], the matrix determinant lemma

det(M+xy⊤)=det(M)+y⊤adj(M)x(2.11)
implies that the characteristic polynomial of L(z) simplifies to
det(Λ1−L(z))=P0(Λ)−igz−1P1(Λ),(2.12)
where
P0(Λ)=det(Λ1−L)(2.13)
is the characteristic polynomial of L, and
P1(Λ)=e⊤adj(Λ1−L)e=tr(adj(Λ1−L)ee⊤).(2.14)

(We note that adj(M) denotes the adjugate matrix of M.) In particular, the characteristic equation of the spectral curve of the system takes the form of a graph of a rational function

z=igP1(Λ)P0(Λ).(2.15)

It follows that if |z| < ∞, then the eigenvector equation (2.6) can always be solved, and the solution has a finite magnitude. This means that all poles of the Baker-Akhiezer function Ω(z) are at z = ∞. The eigenvalues of L(∞) are exactly the eigenvalues of the matrix L due to (2.8). Let us denote these by λ1,...,λn. They form one half of a set of conjugate variables. Since each λj lies on the level set z = ∞, the function z cannot be a conjugate variable to them on the moduli space of all solutions of the system.

A similar situation occurs for the open Toda chain, which was resolved in [17, 2.20b]. In that case one looks for another rational expression which provides the sought-after conjugate variables. For the classical CM system such an expression for conjugate variables was conjectured in [16]. The formula turns out to be again a rational function, depending on the eigenvalues λ1,...,λn, the matrix L, and another matrix X, which, in a suitable basis, has the particle-positions q1,...,qn along its diagonal. The formula was verified using two different approaches, first in [5] and then in [8].

Our aim in the forthcoming sections is to adapt these methods to more general Calogero-Moser systems and the moduli spaces of their solutions. Formally, the resulting formulas for the Calogero-Moser space associated with the cyclic quiver look similar to the classical case [5, 8]. Hence, one may expect that the formulas may hold more generally to Calogero-Moser spaces associated with any “nice” quiver. For a detailed study of the geometry of moment maps for quiver representations, see [4].

3. Calogero-Moser space associated with the cyclic quiver

Let m be a positive integer. In this section we introduce the Calogero-Moser space associated with the affine Dynkin quiver Am−1(1) shown in Figure 1 below.

Fig. 1.

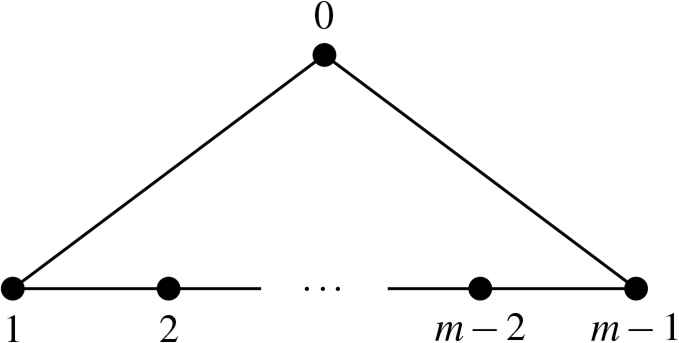
The cyclic quiver.

Starting from this quiver we first take the corresponding doubled quiver. This means that we replace each edge with a pair of edges with opposite orientation to each other. We also equip the quiver with a one-dimensional framing at the vertex 0, and construct the associated Calogero-Moser quiver variety. See Figure 2 for a particular example. The precise procedure of the construction is as follows.

Fig. 2.

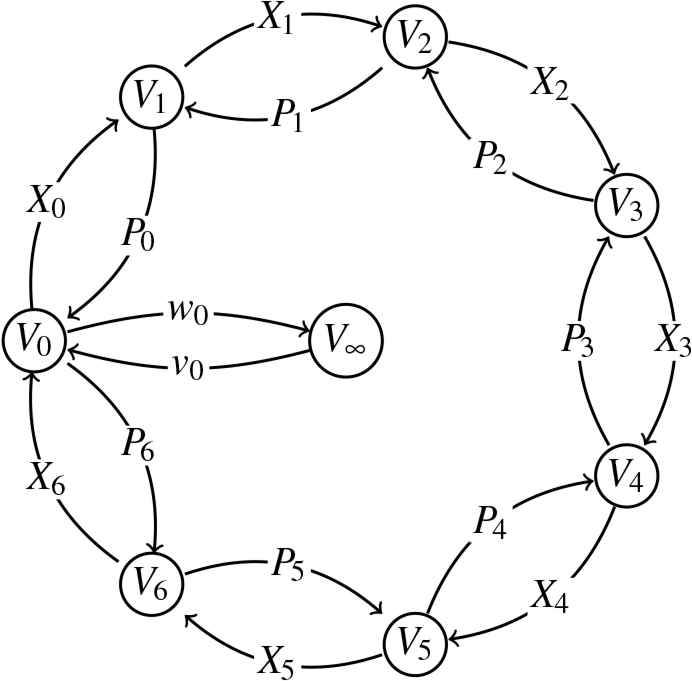
The doubled cyclic quiver for m = 7 with a special framing.

Fix a positive integer n and let V0,V1,...,Vm−1 be vector spaces of dimension n and V∞ be a one-dimensional vector space over the complex field ℂ. Let 𝕑m stand for the additive group 𝕑/m𝕑 of integers modulo m, that is the cyclic group of order m. Let us consider the linear maps

Xi:Vi→Vi+1,   Pi:Vi+1→Vi,   i∈𝕑m(3.1)
and by introducing a one-dimensional vector space V∞ over ℂ we also define the linear maps
v0:V∞→V0,   w0:V0→V∞.(3.2)

Take the direct sum V = V0 ⊕ V1 ⊕ ···⊕ Vm−1 and define the transformations X,P ∈ End(V) by

X(v0⊕v1⊕⋯⊕vm−1)=Xm−1vm−1⊕X0v0⊕…⊕Xm−2vm−2(3.3)
and
P(v0⊕v1⊕⋯⊕vm−1)=P0v1⊕P1v2⊕⋯⊕Pm−1v0.(3.4)

Let 1V denote the identity map on V. The commutator [X,P] ∈ End(V) of X and P can be expressed as

[X,P](v0⊕v1⊕⋯⊕vm−1)=⊕i∈𝕑m(Xi−1Pi−1−PiXi)vi.(3.5)

Extend v0, w0 introduced in (3.2) to maps v: V∞ → V and w: V → V∞, respectively, by

v(z)=v0(z)⊕0V1⊕⋯⊕0Vm−1   and   w(v0⊕v1⊕⋯⊕vm−1)=w0(v0).(3.6)

An m-tuple g =(g0,g1,...,gm−1) ∈ ℂm is called regular if

g0+⋯+gm−1≠0   and   k(g0+⋯+gm−1)≠gh+⋯+gi−1(3.7)
for all k ∈ 𝕑 and 1 ≤ h < i ≤ m − 1. We introduce g1V ∈ End(V) via
g1V(v0⊕v1⊕⋯⊕vm−1)=g0v0⊕g1v1⊕⋯⊕gm−1vm−1.(3.8)

Let Cn,gm stand for the space of quadruples (X, P, v, w) satisfying

[X,P]=g1V+vw.(3.9)

The group GL(V) ⊂ End(V) of invertible linear transformations acts on Cn,gm by

M⋅(X,P,v,w)=(MXM−1,MPM−1,Mv,wM−1),   M∈GL(V).(3.10)

If g is regular, then this action is free. The equivariant Calogero-Moser space Cn,gm for the cyclic group 𝕑m is defined as the space of orbits, i.e.

𝒞n,gm≅Cn,gm/GL(V).(3.11)

In the rest of the paper we will suppress the dependence of Cn,gm on g, and simply write 𝒞nm.

In [3] Chalykh and Silantyev introduced local coordinates on the open dense subset 𝒞nm,X⊂𝒞nm consisting of orbits with invertible and diagonalisable maps Xi. Namely, they diagonalised each of the Xi by choosing such an M ∈ GL(V) that Q = MXM−1, when written in the standard basis, has an m-by-m block matrix structure with blocks of size n. The non-zero blocks are at positions (i + 1,i) and are of the form

q:=[Q]i+1,i=diag(q1,…,qn),   i∈𝕑m.(3.12)

By using the group action and the constraint (3.9) they showed that each point of 𝒞nm,X can be represented by (Q, L, Mv, wM−1) with Q as displayed above and L = MPM−1 having a similar block matrix structure with non-zero blocks at positions (i, i + 1) whose components are

(Li)j,k:=([L]i,i+1)j,k=(pj−ciqj−1)δj,k+|g|qjiqkm−i−1(qjm−qkm)−1(1−δj,k),(3.13)
i ∈ 𝕑m, j,k ∈{1,...,n}, where p1,..., pn are arbitrary and ci, |g| are constants, namely
ci=∑r=0igr−∑s=0m−1m−smgs   and   |g|=∑s=0m−1gs.(3.14)

The maps Mv, wM−1 are expressed as column and row vectors, respectively, with m blocks of size n each. The only non-zero blocks are the first ones, i.e.

[Mv]0=(11…1)⊤   and   [wM−1]0=−|g|(11…1).(3.15)

It was also proved in [3] that these local coordinates (pj/m,qj) are canonical. That is, the symplectic structure on 𝒞nm,X, obtained from the standard symplectic form on 𝒞nm, can be written as

ω=m∑j=1ndpj∧dqj.(3.16)

The Hamiltonians can be written as

Hk(p,q)=1mktr(Lmk),   k=1,…,n,(3.17)
and for m = 1wehave H1(p,q)= H(p,q) (1.2) with γ=−g02.

The same procedure can be repeated by introducing local coordinates (λj, ϕj) on the open dense subset 𝒞nm,P⊂𝒞nm consisting of orbits with diagonalisable maps Pi. We denote the corresponding objects by putting a tilde over them. Namely, we have an invertible transformation M˜∈GL(V) such that the matrix of L˜=M˜PM˜−1 has diagonal blocks at positions (i, i + 1)

λ:=[L˜]i,i+1=diag(λ1,…,λn),   i∈𝕑m,(3.18)
the matrix of Q˜=M˜XM˜−1 has non-zero blocks at positions (i + 1, i)
(Q˜i)j,k:=([Q˜]i+1,i)j,k=(φj+ciλj−1)δj,k−|g|λjm−i−1λki(λjm−λkm)−1(1−δj,k).(3.19)

The maps v˜=M˜v and w˜=wM˜−1 can be written as vectors of size mn with only the first n entries being non-zero:

[v˜]0=(11…1)⊤   and   [w˜]0=|g|(11…1).(3.20)

Finally, the symplectic structure on 𝒞nm,P can be written as

ω˜=m∑j=1ndλj∧dφj.(3.21)
hence the Poisson bracket of two functions f, g ∈ C∞ (𝒞nm,P) is given by
{f,g}=m∑j=1n(∂f∂λj∂g∂φj−∂f∂φj∂g∂λj).(3.22)

The Hamiltonians Hk (3.17), when expressed in terms of (λj, ϕk), take a much simpler form

Hk=1mktr(L˜mk)=1k(λ1mk+⋯+λnmk),   k=1,…,n.(3.23)

4. Canonical spectral coordinates in the spinless case

Now we turn to the task of finding explicit formulas for variables conjugate to the eigenvalues λ1,...,λn of Pi, i.e. such functions θ1,...,θn in involution that

{λj,θk}=δjk,   jk=1,…,n.(4.1)

It follows from (3.22) that the variables ϕ1/m,..., ϕn/m are such functions. Proposition 4.1 below provides explicit formulas for ϕk in terms of λ. To formulate the statement we need the following functions on 𝒞nm that depend on an extra variable z:

A(z)=det(z1V−P),(4.2)
C(z)=tr(Xadj(z1V−P)vw),(4.3)
D(z)=tr(Xadj(z1V−P)).(4.4)

Notice that these functions, besides z, depend only on the class of the quadruple (X,P,v,w) under the GL(V)-action (we have suppressed this dependence). Therefore A,C,D descend to well-defined functions on 𝒞nm for which we use the same notation. Here X,P,v,w are given by (3.3), (3.4), (3.6) and adj denotes the adjugate map. We remark that C(z) can also be written as

C(z)=wXadj(z1V−P)v.(4.5)

Lemma 4.1

The characteristic polynomial A(z)= det(z1V − P) can be written in terms of λ1,...,λn as

A(z)=∏j=1n(zm−λjm).(4.6)

Proof.

[Proof #1] Notice that A(z) is invariant under conjugation, i.e. constant along orbits of GL(V). Thus we can use L˜=M˜PM˜−1 instead of P. Let us express A(z) in the basis in which the matrix of L˜ is the one displayed in (3.18). This means that A(z) can be written as

A(z)=|z1n−λ0…00z1n−λ⋱⋮⋮⋱⋱⋱⋮0⋱⋱⋱−λ−λ0…0z1n|m×m,(4.7)
where the index m × m indicates that the number of blocks in each row and column is m. If we partition the matrix as indicated by the dashed lines and apply the block matrix determinant formula
det[αβγδ]=det(α)det(δ−γα−1β),(4.8)
(with the assumption that z ≠ 0) then we get
A(z)=zn|z1n−λ0…00z1n−λ⋱⋮⋮⋱⋱⋱⋮0⋱⋱⋱−λ−z−1λ20…0z1n|(m−1)×(m−1).(4.9)

By iterating this process (m − 2) times we obtain

A(z)=z(m−2)n|z1n−λ−z−(m−2)λm−1z1n|2×2.(4.10)

Applying the determinant formula (4.8) one more time yields

A(z)=z(m−1)ndet(z1n−z−(m−1)λm)=det(zm1n−λm)=∏j=1n(zm−λjm).(4.11)

This concludes the proof.

Let us give an alternative and more direct proof.

Proof.

[Proof #2] In this proof we partition the matrix the same way as in (4.7), but apply a different version of the block matrix determinant formula, namely

det[αβγδ]=det(δ)det(α−βδ−1γ).(4.12)

This requires the calculation of the determinant and inverse of the bottom right block. Fortunately, this block is an upper triangular matrix of size (m − 1)n. Its determinant is

det(δ)=z(m−1)n,(4.13)
and (with the assumption that z ≠ 0) its inverse exists and is, of course, also upper triangular. The (h,i)-th block of δ−1 is
[δ−1]h,i=zh−i−1λ−i−h,  if  h≤i,   [δ−1]h,i=0n  if  h>i.(4.14)

The product βδ−1γ is simply λ2[δ−1]1,m−1. Substituting everything into (4.12) yields

A(z)=z(m−1)ndet(z1n−z−(m−1)λm)=det(zm1n−λm)=∏j=1n(zm−λjm),(4.15)
which concludes the proof.

Lemma 4.2

The inverse of z1V − P can be written explicitly in terms of λ1,...,λn as an m × m block matrix with blocks of size n of the form

[(z1mn−L˜)−1]h,i=zm−(−i−h+1)(zm−λm)−1λi−h,h,i∈𝕑m,(4.17) (4.16)
where the exponents m − (i − h + 1) and i − h are understood modulo m.

If one does not wish to use mod m exponents one can write [(z1mm−L˜)−1] as

[(z1mn−L˜)−1]h,i=zh−i−1(zm−λm)−1λm−(h−i),   h,i=0,…,m−1,h>i,(4.17)
[(z1mn−L˜)−1]h,i=zm−(i−h+1)(zm−λm)−1λi−h,   h,i=0,…,m−1,h≤i,(4.18)

Proof.

A simple check confirms that the matrix defined by formulas (4.17)–(4.18) is such that (z1mn−L˜)(z1mn−L˜)−1=1mn.

We recall that the adjugate of an invertible linear transformation M can be written as adj(M)= det(M)M−1, hence assuming that z1V − P is invertible we have the following

adj(z1V−P)=A(z)(z1V−P)−1,(4.19)
where A(z)= det(z1V − P) as defined in (4.2).

The next statement gives Theorem 1.1 for the spinless CM space 𝒞nm.

Proposition 4.1.

For a point [(X,P,v,w)]∈𝒞nm,p let

r(z)=D(z)A′(z)∈ℂ(z),(4.20)
where A(z) and D(z) are the functions defined in (4.2) and (4.4), respectively. Then the variables ϕ1,..., ϕn can be expressed as
φk=r(λk),   k=1,…,n.(4.21)

Proof.

Since A(z) and D(z) are both invariant under conjugation by elements of GL(V), using Q˜=M˜XM˜−1 instead of X and L˜=M˜PM˜−1 instead of P in these functions gives the same results. We already expressed A(z) in terms of λ1,...,λn in Lemma 4.1, so let us consider D(z) and calculate the diagonal blocks of Q˜adj(z1mn−L˜). These blocks can be calculated by utilizing (4.19) and Lemma 4.2. Namely, we get

[Q˜adj(z1mn−L˜)]i,i=Q˜i−1A(z)zm−2λ(zm−λm)−1,   i∈𝕑m.(4.22)

The function D(z) can be written in terms of λ1,...,λn as

D(z)=tr(Q˜adj(z1mn−L˜))=∑i=0m−1tr([Q˜adj(z1mn−L˜)]i,i).(4.23)

Plugging (4.22) into this formula gives

D(z)=∑i=0m−1tr(Q˜iA(z)zm−2λ(zm−λm)−1)=∑i=0m−1∑j=1n(φj−ciλj−1)λjzm−2∏ℓ=1(ℓ≠j)n(zm−λℓm).(4.24)

Substituting z = λk causes all terms with j ≠ k to vanish leaving

D(λk)=∑i=0m−1(φk−ciλk−1)λkm−1∏ℓ=1(ℓ≠k)n(λkm−λℓm).(4.25)

Differentiating A(z) with respect to z yields

A′(z)=mzm−1∑j=1n∏ℓ=1(ℓ≠j)n(zm−λℓm),(4.26)
which at z = λk takes the following form
A′(λk)=mλkm−1∏ℓ=1(ℓ≠k)n(λkm−λℓm).(4.27)

Putting formulas (4.25) and (4.27) together gives

D(λk)A′(λk)=1m∑i=0m−1(φk−ciλk−1)=φk+c0+⋯+cm−1mλk.(4.28)

By using (3.14) a simple calculation reveals that c0 + ⋯ + cm−1 = 0 leaving us with

D(λk)A′(λk)=φk(4.29)
and the proof is complete.

Next, we will prove the analogue of Sklyanin’s formula [8, 16] in the equivariant case, which provides another set of variables θ1,...,θn conjugate to λ1,...,λn. The result gives Theorem 1.2 for 𝒞nm.

Proposition 4.2.

For a point [(X,P,v,w)]∈𝒞nm,p let us define the function

s(z)=C(z)|g|A′(z)∈ℂ(z)(4.30)
with A(z) and C(z) defined in (4.2) and (4.3), respectively, and use it to define the variables θ1,...,θn as
θk=s(λk),   k=1,…,n.(4.31)

Then θk can be written as

θk=φkm+fk(λ1,…,λn),   k=1,…,n,(4.32)
with such λ -dependent functions f1,..., fn that
∂fj∂λk=∂fk∂λj,   j,k=1,…,n.(4.33)

In particular, the variables θ1,...,θn given by (4.31) are conjugate to λ1,...,λn, i.e. we have{θj, θk} = 0 and {λj, θk} = δj,k, j, k = 1,...,n.

Proof.

Let us start with C(z). Using gauge invariance we replace the quadruple (X,P,v,w) by (Q˜, L˜, v˜, w˜) just as we did before, to get

C(z)=tr(Q˜adj(z1mn−L˜)v˜w˜)=tr([Q˜adj(z1mn−L˜]0,0[v˜w˜]0,0).(4.34)

Using (4.22) with i = 0 yields

C(z)=tr(Q˜m−1A(z)zm−2λ(zm−λm)−1[v˜w˜]0,0).(4.35)

Since [v˜w˜]0,0 is the n × n matrix that has |g| for all of its components we get

C(z)=|g|∑j,t=1n(Q˜m−1)j,tλtzm−2∏ℓ=1(ℓ≠t)n(zm=λℓm).(4.36)

Substituting z = λk into this expression yields

C(λk)=|g|∑j=1n(Q˜m−1)j,kλkm−1∏ℓ=1(ℓ≠k)n(λkm−λℓm).(4.37)

Putting formulas (4.27) and (4.37) together gives

θk=C(λk)|g|A′(λk)=1m∑j=1n(Q˜m−1)j,k=φkm+fk(λ1,…,λn)(4.38)
with
fk(λ1,…,λn)=cm−1mλk−|g|mλk∑ℓ=1(ℓ≠k)nλkmλkm−λℓm.(4.39)

This implies that {λj,θk} = δj,k, j, k = 1,...,n. The partial derivative of fk with respect to λj (j ≠ k) is

∂fk∂λj=−|g|(λjλk)m−1(λkm−λjm)2,(4.40)
which is clearly invariant under exchanging k and j, and therefore we have
∂fk∂λj=∂fj∂λk(4.41)
entailing {θj, θk} = 0 for all j, k = 1,...,n. This concludes the proof.

5. Calogero-Moser spaces with spin variables and their canonical variables

In this section, we derive the analogues of the results obtained in the previous section to models containing spin variables. Let d be a positive integer. The affine Dynkin quiver Am−1(1) in this case is equipped with a framing of dimension d at each of its vertices, or, equivalently, with one d dimensional framing which is connected to every other node. This latter formulation will be more convenient for us. Accordingly, we redefine the maps v,w (3.6) to be v: ℂdm → V, w: V → ℂdm given by

v(z0,…,zm−1)=v0(z0)⊕v1(z1)⊕⋯⊕vm−1(zm−1)(5.1)
and
w(v0⊕v1⊕⋯⊕vm−1)=(w0(v0),w1(v1),…,wm−1(vm−1)),(5.2)
where vi : ℂd → Vi, wi : Vi → ℂd (i ∈ 𝕑m) are linear maps. Points in the (equivariant) spin Calogero-Moser space are represented by quadruples (X, P, v, w) satisfying
[X,P]=g1V+vw.(5.3)

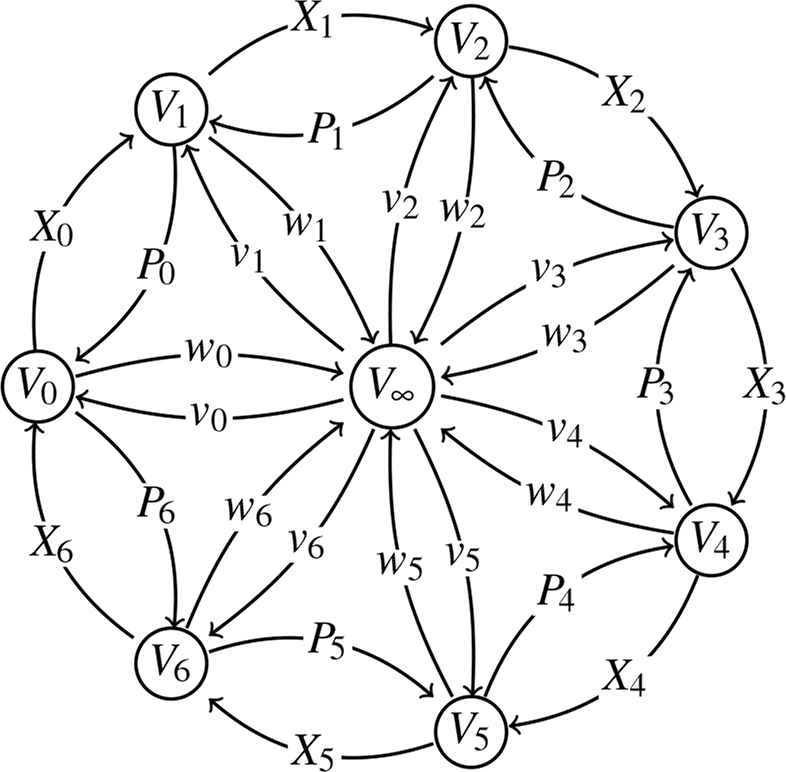
The space itself is denoted as s𝒞nm, where we have suppressed the dependence on the stability vector g as well as on the dimension d of the space of internal states. Two dual models of this space, similar to the ones presented in Section 4, can be given. For details, see [3, Subsection 5.4.].

Fig. 3.

The doubled cyclic quiver for m = 7 with the modified framing.

The objects we are most interested in are the ones corresponding to Q˜, L˜. With a slight abuse of notation, we let Q˜, L˜ denote the spin versions as well. They have the same block matrix structure as previously, but certain non-zero blocks are different. The map L˜ has the same matrix as before, so for non-zero blocks we have

λ=[L˜]i,i+1=diag(λ1,…,λn),(5.4)
while the non-zero blocks of the matrix of Q˜ are given by
(Q˜i)j,j=([Q˜]i+1,i)j,j=φj+λj−1(ci∑r−0i[v˜rw˜r]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j)(5.5)
for i ∈ 𝕑m, j = 1,...,n and
(Q˜i)j,k=([Q˜]i+1,i)j,k=−∑h=0m−1[v˜i−hw˜i−h]j,kλjm−h−1λkhλjm−λkm,(5.6)
for i ∈ 𝕑m, j, k = 1,...,n (j ≠ k). (The index i − h of v˜ and w˜ is understood modulo m.) The maps v˜, w˜ have matrices that satisfy the equation
∑i=0m−1[v˜iw˜i]j,j=|g|(5.7)
for all j = 1,...,n. It was shown in [3, Proposition 6.6] that the local coordinates (λj, ϕj/m, [w˜i]α,j, [v˜i]j,α) on the spin Calogero-Moser space s𝒞nm are canonical, i.e. the reduced symplectic form on s𝒞nm can be locally written as follows
ω˜=∑j=1n(mdλj∧dφj+∑i=0m−1∑α=1d[w˜i]α,j∧[v˜i]j,α).(5.8)

The Poisson bracket of two functions f,g on the spin Calogero-Moser space s𝒞nm can be locally computed via

{f,g}=∑j=1n[m(∂f∂λj∂g∂φj−∂f∂φj∂g∂λj)+∑i=0m−1∑α=1d(∂f∂[w˜i]α,j∂g∂[v˜i]j,α−∂f∂[v˜i]j,α∂g∂[w˜i]α,j)].(5.9)

The expressions of the functions A,C,D on the spin Calogero-Moser space are formally the same as in the spinless case. Namely,

A(z)=det(z1V−P),(5.10)
C(z)=tr(Xadj(z1V−P)vw),(5.11)
D(z)=tr(X adj(z1V−P)).(5.12)

Again, the dependence of them on the class of (X,P,v,w) is suppressed. In the spin case the product vw is understood to be the sum of the tensor (or dyadic) products

vw=⊕i=0m−1viwi,(5.13)
which can also be seen from the alternative expression
C(z)=wXadj(z1V−P)v.(5.14)

The next result gives Theorem 1.1 for the spin case.

Proposition 5.1.

The variables ϕ1,..., ϕn can be expressed using the functions A and D as follows

φk=D(λk)A′(λk),   k=1,…,n.(5.15)

Proof.

Using expression (4.23) we get

D(z)=∑i=0m−1tr(Q˜iA(z)zm−2λ(zm−λm)−1)=∑i=0m−1∑j=1n(Q˜i)j,jλjzm−2∏ℓ=1(ℓ≠j)n(zm−λℓm).(5.16)

Interchanging the order of summation and the identity

∑i=0m−1(ci+∑r=0i[v˜rw˜r]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j)=0,(5.17)
which follows from (5.7), give
D(z)=∑j=1nφjmλjzm−2∏ℓ=1(ℓ≠j)n(zm−λℓm).(5.18)

Substituting z = λk into this formula yields

D(λk)=φkmλkm−1∏ℓ=1(ℓ≠k)n(λkm−λℓm)=φkA′(λk)(5.19)
and the proof is complete.

The next statement completes the proof of Theorem 1.2 in the spin case.

Proposition 5.2.

For a point [(X,P,v,w)]∈s𝒞nm,p let

s(z)=C(z)|g|A′(z)∈ℂ(z)(5.20)
with A(z) and C(z) defined in (5.10) and (5.11), respectively. Let us moreover define the variables θ1,...,θn as
θk=s(λk),   k=1,…,n.(5.21)

Then the variables θ1,...,θn given by the generalized Sklyanin’s formula (5.21) are conjugate to λ1,...,λn.

Proof.

A direct calculation shows that

C(z)=∑i=0m−1∑j,t=1n[v˜iw˜i]t,j(Q˜i−1)j,tλtzm−2∏ℓ=1(ℓ≠t)n(zm−λℓm)(5.22)
hence by using (4.27) θk can be expressed as
θk=1m|g|∑i=0m−1∑j=1n[v˜iw˜i]k,j(Q˜i−1)j,k.(5.23)

Taking (5.5)–(5.7) into account, the variable θk can be explicitly spelled out as

θk=φkm+ek(λk,v˜,w˜)+fk(λ1,…,λn,v˜,w˜),(5.24)
where
ek(λk,v˜,w˜)=1m|g|λk∑i=0m−1[v˜iw˜i]k,k(ci−1+∑r=0i−1[v˜rw˜r]k,k−∑s=0m−1m−sm[v˜sw˜s]k,k),(5.25)
and
fk(λ1,…,λn,v˜,w˜)=−1m|g|∑h,i=0m−1∑t=1(t≠k)n[v˜iw˜i]k,t[v˜i−h−1w˜i−h−1]t,kλtm−h−1λkhλtm−λkm.(5.26)

From (5.9) and (5.24) we get

{λj,θk}=m∂θk∂φj=m1m∂φk∂φj=δj,k.(5.27)

The explicit expression (5.24) lets us decompose {θj,θk} as follows

{θj,θk}=1m2{φj,φk}+1m{φj,ek}+1m{ej,φk}+{ej,ek}+1m{φj,fk}+1m{fj,φk}   +{ej,fk}+{fj,ek}+{fj,fk}.(5.28)

Since ϕj and ϕk Poisson commute and ej depends only on λj, but not the other λ’s, each of the first four terms on the right-hand side is zero, that is

{φj,φk}=0,   {φj,ek}=0,   {ej,φk}=0,   {ej,ek}=0.(5.29)

Hence we are left with

{θj,θk}=1m({φj,fk}+{fj,φk})+{ej,fk}+{fj,ek}+{fj,fk},(5.30)
where the terms we grouped cancel, because for every j, k = 1,...,n, we have
{fj,φk}+{φj,fk}=∂fk∂λj−∂fj∂λk=0.(5.31)

Indeed, we have

∂fj∂λk=−1m|g|∑h,i=0m−1[v˜iw˜i]j,k[v˜i−h−1w˜i−h−1]k,j∂∂λkλkm−h−1λjhλkm−λjm(5.32)
and a straightforward calculation shows that
∂∂λkλkm−h−1λjhλkm−λjm=∂∂λjλjh+1λkm−h−2λjm−λkm.(5.33)

Thus

∂fj∂λk=−1m|g|∑h,i=0m−1[v˜iw˜i]j,k[v˜i−h−1w˜i−h−1]k,j∂∂λjλjh+1λkm−h−2λjm−λkm.(5.34)

Rewriting the sum using a new pair of indices h′, i′ given by

h′≡m−h−2   (mod  m)i′≡i−h−1   (mod   m)(5.35)
we get
∂fj∂λk=−1m|g|∑h′,i′=0m−1[v˜i′w˜i′]k,j[v˜i′−h′−1w˜i′−h′−1]j,k∂∂λjλjm−h′−1λkh′λjm−λkm,(5.36)
which, by an exchange of j and k in (5.32), can be seen to coincide with ∂fk/∂λj. As a consequence, we now have
{θj,θk}={ej,fk}+{fj,ek}+{fj,fk}.(5.37)

Let us consider the first term on the right-hand side. Since ej and fk do not depend on any of the ϕ’s and ej only depends on the j-th column (resp. row) of [w˜i] (resp. [v˜i]) we have

{ej,fk}=∑i=0m−1∑α=1d(∂ej∂[w˜i]α,j∂fk∂[v˜i]j,α−∂ej∂[v˜i]j,α∂fk∂[w˜i]α,j).(5.38)

A straightforward computation yields

∂ej∂[w˜i]α,j=1m|g|λj[[v˜i]j,α(ci−1+∑r=0i−1[v˜rw˜r]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j)   −m−im[v˜i]j,α∑h=0m−1[v˜jw˜h]j,j+[v˜j]j,α∑h=i+1m−1[v˜iw˜i]j,j].(5.39)

Collecting the common factor [v˜i]j,α and applying (5.7) give us

∂ej∂[w˜i]α,j=[v˜i]j,αm|g|λj[ci−1+im|g|−[v˜iw˜i]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j].(5.40)

Similarly,

∂ej∂[v˜i]j,α=[w˜i]α,jm|g|λj[ci−1+im|g|−[v˜iw˜i]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j].(5.41)

As for the partial derivatives of fk,we have

∂fk∂[w˜i]α,j=−[v˜i]k,αm|g|∑h=0m−1[v˜i−h−1w˜i−h−1]j,kλjm−h−1λkhλjm−λkm(5.42)
and
∂fk∂[v˜i]j,α=−[w˜i]α,km|g|∑h=0m−1[v˜i+h+1w˜i+h+1]k,jλjm−h−1λkhλjm−λkm.(5.43)

Putting formulas (5.40)–(5.43) together, {ej, fk} (5.38) is found to be

{ej,fk}=1(m|g|)2∑h,i=0m−1([v˜iw˜i]k,j[v˜i−h−1w˜i−h−1]j,k−[v˜iw˜i]j,k[v˜i+h+1w˜i+h+1]k,j)×   ×(ci−1+im|g|−[v˜iw˜i]j,j−∑s=0m−1m−sm[v˜sw˜s]j,j)λjm−h−2λkhλjm−λkm.(5.44)

The Poisson bracket {fj,ek} is obtained from {ej, fk} (5.44) by changing its sign and exchanging j and k. Hence we get

{fj,ek}=1(m|g|)2∑h′,i=0m−1([v˜iw˜i]k,j[v˜i+h′+1w˜i+h′+1]j,k−[v˜iw˜i]j,k[v˜i−h′+1w˜i−h′+1]k,j)×   ×(ci−1+im|g|−[v˜iw˜i]k,k−∑s=0m−1m−sm[v˜sw˜s]k,k)λkm−h′−2λjh′λjm−λkm.(5.45)

Rewriting this using the new index h ≡ m − h′− 2 (mod m) allows us to collect the factors of the terms with the same λ dependence in {ej, fk} and {fj,ek}. Then we add (5.44) and (5.45) together and find that the terms with ci and im|g| cancel and as a result, we get

{ej,fk}+{fj,ek}=1(m|g|)2λjλk∑h=1m−1∑i=0m−1([v˜iw˜i]k,k−[v˜iw˜i]j,j)×   ×([v˜iw˜i]k,j[v˜i−hw˜i−h]j,k−[v˜iw˜i]j,k[v˜i+hw˜i+h]k,j)λjm−hλkhλjm−λkm.(5.46)

Let us now consider the last term {fj, fk} in {θj, θk} (5.37). Since fj and fk do not depend on any of the ϕ’s we have

{fj,fk}=∑ℓ=1n∑i=0m−1∑α=1d(∂fj∂[w˜i]α,ℓ∂fk∂[v˜i]ℓ,α−∂fj∂[v˜i]ℓ,α∂fk∂[w˜i]α,ℓ).(5.47)

We already calculated most of these partial derivatives in (5.42) and (5.43). The only ones remaining are

∂fj∂[w˜i]α,j=−1m|g|∑t=1(t≠j)n[v˜i]t,α∑h=0m−1[v˜i+h+1w˜i+h+1]j,tλtm−h−1λjhλtm−λjm(5.48)
and
∂fj∂[v˜i]j,α=−1m|g|∑t=1(t≠j)n[w˜i]α,t∑h=0m−1[v˜i−h−1w˜i−h−1]t,jλtm−h−1λjhλtm−λjm.(5.49)
for α = 1,...,d. Now we break up the sum (5.47) into six parts, namely
{fj,fk}=∑ℓ=1(ℓ≠j,k)n∑i=0m−1∑α=1d∂fj∂[w˜i]α,ℓ∂fk∂[v˜i]ℓ,α︸=:A−∑ℓ=1(ℓ≠j,k)n∑i=0m−1∑α=1d∂fj∂[v˜i]ℓ,α∂fk∂[w˜i]α,ℓ︸=:B   +∑i=0m−1∑α=1d∂fj∂[w˜i]α,j∂fk∂[v˜i]j,α︸=:C−∑i=0m−1∑α=1d∂fj∂[v˜i]j,α∂fk∂[w˜i]α,j︸=:D   +∑i=0m−1∑α=1d∂fj∂[w˜i]α,k∂fk∂[v˜i]k,α︸=:E−∑i=0m−1∑α=1d∂fj∂[v˜i]k,α∂fk∂[w˜i]α,k︸=:F.(5.50)

Fortunately, these expressions are related. For example, we get B if we exchange j and k in A. We denote this by writing that B =(A)j↔k. There are similar relations between the expressions C and F, as well as between the expressions D and E. In short, we have

B=(A)j↔k,C=(F)j↔k,D(E)j↔k.(5.51)

This observation saves us half the work as we only need to calculate, say A, F, and E. First, we calculate A and find that

A=1(m|g|)2∑ℓ=1(ℓ≠j,k)n∑i,h,h′=0m−1[v˜iw˜i]j,k[v˜i−h−1w˜i−h−1]ℓ,j[v˜i+h′+1w˜i+h′+1]k,ℓλℓ2m−h−h′−2λjhλkh′(λℓm−λℓm)(λℓm−λkm).(5.52)

Second, we calculate F and get

F=1(m|g|)2∑ℓ=1(ℓ≠k)n∑i,h,h′=0m−1[v˜iw˜i]ℓ,j[v˜i+h+1w˜i+h+1]k,ℓ[v˜i+h′+1w˜i+h′+1]j,kλℓm−h−1λkm−h′−1λjh′(λℓm−λkm)(λkm−λjm).(5.53)

Third, we calculate E and get

E=1(m|g|)2∑ℓ=1(ℓ≠k)n∑i,h,h′=0m−1[v˜iw˜i]j,ℓ[v˜i−h−1w˜i−h−1]ℓ,k[v˜i−h′−1w˜i−h′−1]k,jλℓm−h−1λkm−h′−1λjh′(λℓm−λkm)(λkm−λjm).(5.54)

We obtain explicit formulas for B, C, and D from (5.52)–(5.54) and the relations (5.51). Namely,

B=1(m|g|)2∑ℓ=1(ℓ≠j,k)n∑i,h,h′=0m−1[v˜iw˜i]k,j[v˜i−h′−1w˜i−h′−1]ℓ,k[v˜i+h+1w˜i+h+1]j,ℓλℓ2m−h−h′λjhλkh′(λℓm−λjm)(λℓm−λkm),(5.55)
C=1(m|g|)2∑ℓ=1(ℓ≠j)n∑i,h,h′=0m−1[v˜iw˜i]ℓ,k[v˜i+h+1w˜i+h+1]j,ℓ[v˜i+h′+1w˜i+h′+1]k,jλℓm−h−1λjm−h′−1λkh′(λℓm−λjm)(λjm−λkm),(5.56)
and
D=1(m|g|)2∑ℓ=1(ℓ≠j)n∑i,h,h′=0m−1[v˜iw˜i]k,ℓ[v˜i−h−1w˜i−h−1]ℓ,j[v˜i−h′−1w˜i−h′−1]j,kλℓm−h−1λjm−h′−1+hλkh′(λℓm−λjm)(λjm−λkm).(5.57)

By a suitable change of indices in D and F we see that in A−D−F almost all terms cancel. The only ones remaining are the terms with ℓ = k in D and the terms with ℓ = j in F. As a consequence, we get

A−D−F=1(m|g|)2∑i,h,h′=0m−1([v˜iw˜i]k,k[v˜i−h−1w˜i−h−1]k,j[v˜i−h′−1w˜i−h′−1]j,k+   +[v˜iw˜i]j,j[v˜i+h′+1w˜i+h′+1]k,j[v˜i+h+1w˜i+h+1]j,k)λℓm−h′−1λkm−h−1+h′(λjm−λkm)2.(5.58)

With the same type of computation we obtain

−B+C+E=−1(m|g|)2∑i,h,h′=0m−1([v˜iw˜i]k,k[v˜i+h′+1w˜i+h′+1]k,j[v˜i+h+1w˜i+h+1]j,k+   +[v˜iw˜i]j,j[v˜i−h−1w˜i−h−1]k,j[v˜i−h′−1w˜i−h′−1]j,k)λjm−h′−1+hλkm−h−1+h′(λjm−λkm)2.(5.59)

Since the exponents of λj and λk do not depend on i and depend only on the difference of h and h′, but not on the individual indices, introducing a new index h″:= h − h′ and adding (5.58) to (5.59), yields an explicit formula for the Poisson bracket {fj, fk}. Namely, we get

{fj,fk}=−1(m|g|)2λjλk∑h″=1m−1∑i=0m−1([v˜iw˜i]k,k−[v˜iw˜i]j,j)×   ×([v˜iw˜i]k,j[v˜i−h″w˜i−h″]j,k−[v˜iw˜i]j,k[v˜i+h″w˜i+h″]k,j)λjm−h″λkh″λjm−λkm.(5.60)

This is the same expression as (5.46) only with opposite sign. Hence these two terms in {θj, θk} cancel and we obtain

{θj,θk}=0.(5.61)

Finally, let us observe that due to (5.7) we can take any fixed h ∈ 𝕑m and β ∈ {1,...,d} and express [v˜h]j,β in terms of [v˜i]j,α and [w˜i′]α′,j with i,i′ ∈ 𝕑m (i ≠ h) and α, α′ ∈ {1,...,d} (α ≠ β) for all j = 1,...,n. This means that [v˜h]j,β(j=1,…,n) are not independent coordinates on s𝒞mn, thus

{θk,[v˜h]j,β}=0   {θk,[w˜h]β,j}=0(5.62)
for all j,k = 1,...,n.

Remark 5.1.

Let us list some important special cases of our results. In [3], it was shown that the m = 2, d = 1 case corresponds to the rational Calogero-Moser system of type Bn (and with g1 = 0 of type Dn). Setting m = 1, d > 1 produces the Gibbons-Hermsen system [6], whereas the m = 2, d > 1 case contains the type Bn variant of the Gibbons-Hermsen system.

6. The equivariant geometry of the interpolation curves

Now we briefly describe the geometry of the interpolation curves appearing in Theorems 1.1 and 1.2. These are the affine plane curves

C1={(z,r(z)):z∈ℂ}⊂ℂ2   and   C2={(z,s(z)):z∈ℂ}⊂ℂ2.(6.1)

Both of these are rationally parametrized. Hence, they can be completed to rational curves in ℂ𝕇2. The expressions (4.26), (4.36), (5.22), (4.24) and (5.18) show that the polynomials A′(z), C(z) and D(z) in all cases are divisible by zm−2. After cancellations we can write

r(z)=:p1(zm)zq(zm)   and   s(z)=:p2(zm)zq(zm),(6.2)
where p1(z), p2(z) and q(z) are polynomials of degree n − 1. The defining equation of the curve Cδ is
q(zm)zy−pδ(zm)=0,   δ=1,2.(6.3)

Let Δ be the root system Am−1 and let us choose a primitive m-th root of unity ω. There corresponds to Δ a subgroup GΔ of SL(2, ℂ), a cyclic subgroup of order m, which is generated by the matrix

σ=(ω00ω−1).(6.4)

All irreducible representations of GΔ are one-dimensional, and are given by ρj : σ ↦ ωj, for j ∈ 𝕑m. The corresponding McKay quiver is the cyclic Dynkin diagram of type A˜m−1(1). The group GΔ acts on ℂ2; the quotient variety ℂ2/GΔ has an isolated singularity of type Am−1 at the origin. In coordinates, the ring of functions H0(𝒬ℂ2/GΔ)= ℂ [y,z]GΔ is generated by a = zm, b = ym and c = zy which satisfy the relation

ab=cm.(6.5)

As it was remarked in [3, Section 5.1] the set of eigenvalues (λ1m,…,λnm) of the transformation P0P1 ...Pm−1 ∈ End(V0) determines (λ1,...,λn) only up to permutations and multiplication by m-th root of unity. Therefore, the coordinates λi, ϕi are only well-defined up to the action of Sn ⋉ GΔ, where the Sn component permutes {λi} and {ϕi} simultaneously, and the generator of the GΔ component maps (λi, ϕi) to (ωλi,ω−1ϕi).

The following lemma is straightforward from (4.32) and (5.24).

Lemma 6.1

When λi is replaced by ωλi, then θi is replaced by ω−1θi. Therefore, the coordinates λi, θi are also well-defined only up to the action of Sn ⋉ GΔ.

Corollary 6.1.

The pairs of variables (λi,ϕi) and (λi,θi) are well-defined on ℂ2/GΔ.

As a result, the curves C1 and C2 are only well-defined up to the action of GΔ. But they descend to well-defined curves on the quotient space ℂ2/GΔ.

Corollary 6.2.

The curves C1 and C2 descend to well-defined rational curves C1/GΔ and C2/GΔ on ℂ2/GΔ. When considered as a subvariety of ℂ3 = Spec(ℂ [a,b,c]),C1/GΔ and C2/GΔ are given by the intersection of the surface (6.5) and the surface

q(a)c−pδ(a)=0,   δ=1,2,(6.6)
respectively, or equivalently, the surface swept out by the translations of the graph of the degree n − 1 interpolating function
c=pδ(a)q(a),   δ=1,2(6.7)
in the b-direction. In this way we obtain a map
𝒞nm→RatCurvesn(ℂ2/GΔ)(6.8)
defined on the dense open subset 𝒞nm,P⊂𝒞nm, where RatCurvesn (ℂ2/GΔ) is the space of rational curves of degree n on ℂ2/GΔ.

Conversely, if C ⊂ℂ2/GΔ is a rational curve of degree n which is of the above form, then any distinct n points on it determine a point of 𝒞nm,P, such that the associated curve Cδ /GΔ (resp. C2/GΔ) to this point is C. This correspondence associates the point of 𝒞nm with coordinates {(λi,ϕi)} (resp. {(λi,θi)}) to the n points {(λi, ϕi)}⊂ C (resp. {(λi,θi)} ⊂ C).

Acknowledgements

We would like to thank Jim Bryan, Maxime Fairon, and Balázs Szendrői for helpful comments and discussions.

This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 795471.

References

[16]E. Sklyanin, 2009. Bispectrality and separation of variables in multiparticle hypergeometric systems, talk given at the ‘Quantum Integrable Discrete Systems‘ Workshop, held at Cambridge, England, March 23-27
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
Journal of Nonlinear Mathematical Physics
Volume-Issue
27 - 2
Pages
243 - 266
Publication Date
2020/01/27
ISSN (Online)
1776-0852
ISSN (Print)
1402-9251
DOI
10.1080/14029251.2020.1700634How to use a DOI?
Copyright
© 2020 The Authors. Published by Atlantis and Taylor & Francis
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Tamás Görbe
AU  - Ádám Gyenge
PY  - 2020
DA  - 2020/01/27
TI  - Canonical spectral coordinates for the Calogero-Moser space associated with the cyclic quiver
JO  - Journal of Nonlinear Mathematical Physics
SP  - 243
EP  - 266
VL  - 27
IS  - 2
SN  - 1776-0852
UR  - https://doi.org/10.1080/14029251.2020.1700634
DO  - 10.1080/14029251.2020.1700634
ID  - Görbe2020
ER  -