Decision Support for Project Rescheduling to Reduce Software Development Delays based on Ant Colony Optimization
- DOI
- 10.2991/ijcis.11.1.68How to use a DOI?
- Keywords
- Decision Support; Ant Colony Optimization; Project Management; Rescheduling; Optimization
- Abstract
Delays often occur during some activities in software development projects. Without handling of project delays effectively, many software development projects fail to meet their deadlines. If extra employees with same or similar skills and domain knowledge can be rescheduled for the remaining activities of the delayed projects, it can be possible to reduce or even eliminate existing delays in concurrent software development projects of similar nature. However, it is evident that employee rescheduling may result in delaying other activities, which may lead to the problem of delay propagation. Hence, it is important to investigate how to reduce or even eliminate the delay in one project without impacting other projects. By nature this is an NP-hard problem. Therefore, we propose a novel generic rescheduling strategy based on adaptive ant colony optimization algorithm to provide decision support for software project managers to select appropriate employees to deal with project delays. We have carried out a set of comprehensive experiments to evaluate the performance of the proposed strategy. In addition, three real world software project instances are also utilized to evaluate our strategy. The results show that our strategy is effective, efficient and able to outperform its representative counterparts significantly.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. INTRODUCTION
Currently, many software companies such as IBM and SAP provide dedicated solutions for specific fields by designing such as universal business flows. The final customized software products for different customers have similar structures and functions, for examples, Financial Management Systems, Customer Relationship Management Systems and Ecommerce Websites. For concurrent customer’s orders, a company needs to organize corresponding project teams of employees possessing same or similar skills and domain knowledge (skill for short in this paper is defined as ability for completing one activity rather than general skill such as C++ programming or Java programming). Customers expect that their orders can be delivered by agreed deadlines, however, delays often occur in software development projects for various reasons such as rework, abandonment and erroneous or uncertain initial estimates according to Ref. 1. Serious delay can make customers very unsatisfied which can damage a company’s reputation and profit. In order to reduce or eliminate delays in software development projects, employees are often forced to work overtime. However, working longer hours is likely to cause fatigue and dissatisfaction among employees. As a result, software quality may also be jeopardized. In this paper, we assume that employees can be re-allocated but working overtime is prohibited. Therefore, it is important to find out how to reduce or even eliminate delays without requesting employees working overtime.
In practice, according to Ref. 2, project planning models for scheduling are based on CPM (Critical Path Method) or PERT (Program Evaluation Review Technique). Based on Ref. 3, project network model has four key parameters for one activity. They are the early start time, early finish time, late start time and late finish time respectively. Therefore, any activity in a project can propagate delay if its real finish time exceeds its late finish time. If delay has not been properly handled along the line, it will be eventually propagated into the final deadline. In order to block delay propagation, how to handle delay for remaining activities in the delayed projects (called delayed activities in this paper) becomes a key issue. In general, resource (i.e. employees in this paper) rescheduling is a promising approach for handling delays. But the challenge is to decide who should be requested to handle the delayed activities. According to one of the software engineering principles in Ref. 4, adding inexperienced persons would cause further delay due to the learning curve and extra communication overhead. However, this research aims at reallocating skilled employees among concurrent projects of similar nature for solving such an issue to minimize, if not entirely avoid, the learning curve and extra communication overhead. In our scenario, multiple concurrent similar software development projects can provide skilled employees. If employees from other concurrent projects with the same skills are available, they can be reallocated across the projects without much learning curve and extra communication overhead. For one example, one employee is assigned to conduct multiple activities. When the activity she/he currently works on is delayed, other subsequent activities which she/he will be working on can be delayed as well. Hence, it becomes necessary that other employees with same skills to be reallocated to help with these delayed activities. For another example, one delayed activity can be handled by a replacement employee possessing the same skill with higher productivity. By doing so, the delay may be reduced or even eliminated. However, due to employee reallocation, a potential problem is that other concurrent projects may be impacted by such as reducing the delay in one project causing delays in other projects. In practice, it is difficult for managers to rely on their experiences to make appropriate decision for rescheduling employees. To address the abovementioned problems, we propose a novel generic decision-making strategy based on adaptive ant colony optimization (ACO) algorithm with three rescheduling rules. Our proposed strategy provides decision support for software project managers to reallocate employees for concurrent projects in order to reduce or even eliminate the delay in the current project without jeopardizing the deadlines of other projects. Based on simulations of benchmark project networks available from well-known PSPLIB from Ref. 5 with randomized parameters such as durations for activities and skills of employees, the experimental results demonstrate that our proposed strategy is very effective, efficient and can achieve better performance than other representative strategies.
In this paper, we have the following major contributions:
- 1.
All software development activities are treated without constraints now.
- 2.
Employees can now have multiple skills as they should possess.
- 3.
A general multi-fork tree is defined for searching feasible solutions.
- 4.
A generic decision-making strategy based on adaptive ACO is proposed to help select appropriate employees to be assigned to the delayed activities.
- 5.
A set of comprehensive experiments is conducted to evaluate the performance of the proposed strategy.
The remainder of this paper is organized as follows. Section 2 introduces related work. Section 3 describes the problem formulation. Section 4 proposes our strategy. Section 5 presents the evaluation. Section 6 concludes our contributions and points out future work.
2. RELATED WORK
Resource scheduling is an effective method for optimizing complex practical problem. In software project development and management area, the Project Scheduling Problem (PSP) has always been a research hot spot. As explained in Ref. 6, project scheduling “involves separating the total work involved in a project into separate activities and judging the time required to complete these activities. Usually, some of these activities are carried out in parallel. Project schedulers must coordinate these parallel activities and organize the work so that the workforce is used optimally”. Clearly, PSP is a typical NP-hard problem and hence many metaheuristics based scheduling algorithms have been employed. According to Ref. 7, metaheuristics include methods to solve search and optimization problems inspired by the biological principles of selection and the collective intelligence of natural systems such as Genetic Algorithm (GA) or ACO. In this section, we present an overview of several representative approaches. Authors of Ref. 8 propose a multi-skill scheduling model which considers some key factors such as skill proficiency of employees and resource conflict. Authors of Ref. 9 use GA to solve the general project scheduling problem. Authors of Ref. 10 discuss estimated schedules and project scheduling based on GA. They propose a two-stage probabilistic scheduling strategy, which aims to decrease schedule overruns. Authors of Ref. 11 propose a new design based on GA to solve the PSP problem based on problem formation proposed in Ref. 9. In their approach, normalization of dedication values is proposed to remove the problem of overwork. Authors of Ref. 12 present a value-based human resource scheduling method among multiple software projects by using GA. Besides GA, ACO is also popular in solving PSP. Ref. 13 shows that the software project scheduling problem (SPSP) can be naturally converted into a graph-based search problem. Therefore, ACO is suitable for solving the problem. Its experiments reveal that the ACO algorithm outperforms the GA approach for the SPSP. Authors of Ref. 14 propose a new scheduling strategy based on event-based scheduler and the ACO algorithm is applied to search feasible solution for a single project. Authors of Ref. 15 propose Multi-objective Evolutionary Algorithm using decomposition and Ant Colony (MOEA/D-ACO) to minimum cost and duration for the SPSP problem. The experiments show that MOEA/D-ACO can obtain solutions with much less time for all instances and outperforms NSGA-II (Non-dominated Sorting Genetic Algorithm-II) with less duration for most of test instances.
From the above, we can see that most related work mainly discusses how to apply GA or basic ACO strategy to solve the scheduling problem. In order to primarily save time for software companies during the planning stage. However, the problem that we investigate is that delays often occur during the development stage. How to handle project delays in the context of development stage across multiple projects has not been well addressed in the literature. In addition, during the planning stage all activities need to be scheduled. During the development stage not all activities need to be rescheduled (activities where no delay occurs do not need to be rescheduled). Otherwise it may easily lead to further delay. Authors in Ref. 1 propose a tandem genetic algorithm to reduce project completion date. In the paper, firstly for a given staffing level and a random or uniform people distribution across teams, an optimal WPs (work packages) ordering is determined. Then for the given staffing level and WPs ordering previously determined, an optimal organization of teams is computed. Authors of Ref. 16 propose a multi-objective evolutionary algorithm based proactive-rescheduling method to address four objectives of project cost, duration, robustness and stability simultaneously when facing disruptions. However, these two papers only discuss reallocation under single project while multiple projects are not considered. In addition, the scale of instances is relative small in Ref. 16 where at most 40 tasks are applied to verify the proposed strategy for one instance. In our experiment, each project can have many more activities. In Ref. 17, a very preliminary ACO-based scheduling strategy is proposed which can only handle delay in some simple cases. Then in Ref. 18, how to reschedule employee in multiple concurrent projects in order to reduce overall penalty of all projects without any overtime is very briefly discussed.
3. PROBLEM FORMULATION
Our problem formulation is originated from the work presented in Ref. 9. Assume there is given a set of projects P1 ….Pn; a set of employees e1 ….eq and a set of skills skill1 ….skillp respectively; a set of activities a1i⋯asi where i again indicates the activity coming from the ith project; an activity precedence graph – a directed graph with activities as nodes and activity precedence as edges.
Here our graph is slightly different to its counterpart in Ref. 9. In order to conveniently reallocate employees and monitor the time change of activities, we further breakdown the activity defined in Ref. 9 as: (1) one activity requires only one skill and is conducted by only one employee; (2) each activity is atomic activity which has no sub-activities. To reflect the real world, we set that an employee may have more than one skill and conduct several activities in the project(s). In addition, we emphasize again that no employee working overtime is required.
Let us give a simple example to illustrate how to make decision to select an appropriate employee in order to find feasible solutions, i.e. delay is reduced or even eliminated at one project while another project is not impacted.
Suppose there are two projects P1 and P2. P1 has two activities a11 and a21 has two activities a12, a22. We assume that Monday is set as the first day of the planning agenda in our example. Though no overtime is allowed, the block with text in red indicating weekends is included in figures. The corresponding activity precedence graph is shown in Fig. 1.

Activity precedence graph of P1 and P2.
All parameters of these two projects are listed in Table 1.
| P1 | Scheduled start time and end time | Duration (planned) | Employee (planned) | Skill Required |
| a11 | From the 3rd day to the 8th day (2 days weekend) | 4 days | e1 | skill1 |
| a21 | From the 9th day to the 11th day | 3 days | e1 | skill2 |
| (a) | ||||
| P2 | Scheduled start time and end time | Duration (planned) | Employee (planned) | Skill Required |
| a12 | From the 4th day to the 8th day (2 days weekend) | 3 days | e2 | skill3 |
| a22 | From the 9th day to the 9th day | 1 day | e3 | skill4 |
| (b) | ||||
Duration of each activity of projects P1 & P2
Suppose that for some reasons, employee e1 is absent on the 3rd day and returns on the 5th day. So the start time of a11 is delayed to the 5th day. The deadline of P1 will be delayed to the 15th day. Meanwhile, the current finish time of P2 is the 9th day. Table 2 lists the skills possessed by each employee.
| Employee | skills |
|---|---|
| e1 | skill1;skill2; |
| e2 | skill3;skill1;skill2; |
| e3 | skill4;skill2; |
Skills of employees (P1 & P2)
We illustrate how to reschedule employees between the two projects in order to reduce the delay of P1 as much as possible without jeopardizing P2. The specific parameters are listed in Table 3.
| e1 | e2 | e3 | |
|---|---|---|---|
| a11 | 4 days | 4 days | N/A |
| a21 | 3 days | 1 day | 8 days |
| a12 | N/A | 3 days | N/A |
| a22 | N/A | N/A | 1 day |
Duration of activity with help (P1 & P2)
Firstly we describe precedence relations and time parameters of activities for projects P1 and P2.
Project P1:
Duration of project P1 is from the 3rd day to the 11th day. Fig. 1 shows that activity a11 with skill1 is the predecessor of a21 with skill2. Employee e1 is shared by the two activities. Based on the parameters listed in Table 1, the planned schedule of a11 is from the 3rd day to the 8th day. It includes two days weekend. The duration of employee e1 conducting a11 is 4 days. The planned schedule of a21 is from the 9th day to the 11th day. The duration of employee e1 conducting a21 is 3 days.
Project P2:
Duration of project P2 is from the 4th day to the 9th day. Based on the parameters listed in Table 1, the planned schedule of a12 with skill3 is from the 4th day to the 8th day. It includes two days weekend. Employee e2 is allocated to work on the activity. Its duration is 3 days. Fig. 1 shows activity a22 with skill4 is the immediate successor of a12 with skill3. The planned schedule of a22 with employee e3 is from the 9th day to the 9th day. Its duration is 1 day.
Delay analysis:
Due to the absence of employee e1, the start time of a11 is delayed to the 5th day. The end time of a11 will be the 10th day, i.e. activity a11 is delayed. Activity a21 must wait until a11 is finished. Its start time is delayed until the 11th day and the end time will be the 15th day. Obviously the end time of a21 exceeds planned finish time of P1. Project P1 will be delayed into the 15th day. Note that the current finish time of P2 is the 9th day. Then our problem is how to handle the delay of project P1. Two different strategies below are illustrated.
First strategy:
The strategy is shown in Fig. 2. Because employee e2 has skill1, we firstly can reallocate employee e2 to conduct a11. So a11 can run from the 3rd day. According to the parameters listed in Table 3, duration of a11 with e2 is 4 days. Due to the two days weekend, the end time of a11 would be the 8th day. Meanwhile, employee e1 has return on the 9th day and can conducts activity a21.

First strategy
Activity a21 can run from the 9th day on schedule. According to the parameters listed in Table 3, the duration of a21 with e1 is 3 days. Its end time is the 11th day. The delay is eliminated for P1 but is transferred to P2. More specifically, since e2 is transferred to a11, a12 must wait until a11 is finished. So the delay would occur at a12. The start time of activity a12 will be postponed to the 9th day. But because activity a12 cannot be helped due to lack of skilled employees, the end time of activity a12 is the 11th day and the delay would be further propagated to its subsequent activity. Since activity a22 is the immediate successor of a12, its start time will be delayed to the 12th day and the end time is the 12th day. Obviously delay is introduced in project P2. Therefore, this strategy is not desirable. Our goal is that the delay of P1 is reduced or even eliminated without P2 being impacted.
Second strategy:
We change the strategy as shown in Fig. 3. Suppose a11 runs without any help which means that the delay is fully propagated to a21. Meanwhile, a12 is finished on schedule. Its end time is the 8th day. Since e2 has skill2, the employee can replace e1 to carry out activity a21 on the 11th day. According to Table 3, duration of activity a21 with e2 is 1 day. The end time of activity a21 is the 11th day. Therefore, the delay is eliminated in project P1 and no delay is introduced to project P2, i.e. no impact to P2. Clearly this is a better rescheduling strategy.
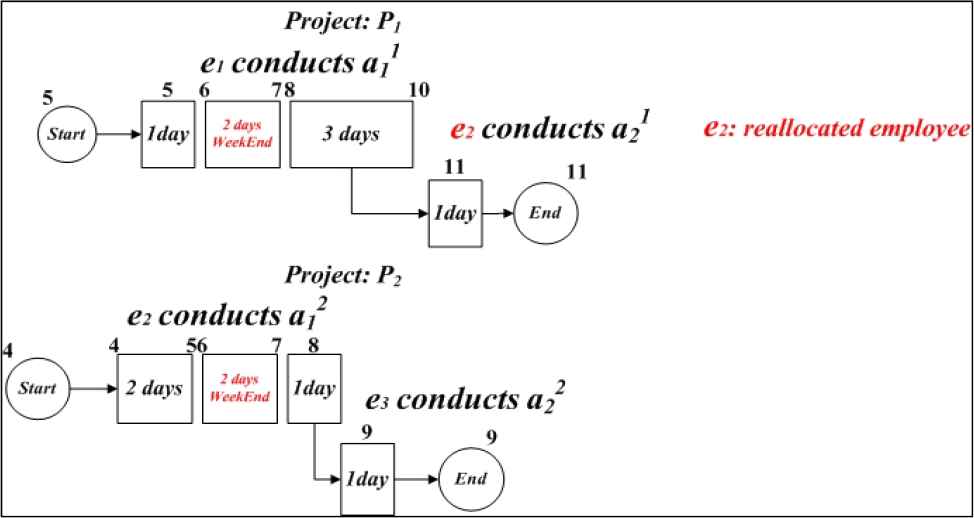
Second strategy
From the above simple illustration, we can conclude that not all delayed activities need to involve immediate rescheduling. In our case, if we handle delay at a11 firstly, the delay at project P2 will be introduced although the delay at project P1 is eliminated. Therefore, sometimes we may need to propagate the delay where a feasible solution can be found.
According to the above analysis, we use notations to denote the rescheduling process, i.e. (ex→ayn) indicates that employee ex is selected to conduct activity ayn. In addition, since some activities may share one employee, those activities must execute in sequence. Now we can use the notation to describe the entire second strategy: e.g. < (e1→a11), (e2→a12), (e2→a21), (e3→a22)>. Here since employee e2 is shared by activities a12 and a21, a12 precedes a21.
Based on the example, we find that there are two choices when an activity gets delayed. One choice is that the activity is executed by the original employee, i.e., a delay is propagated to its subsequent activities. Another choice is that the activity is executed by another employee with the same skill. Different choices for handling delay of an activity can lead to different results. For instance, at activity a11, in the first strategy, it chooses to reschedule employee e2 to handle the delay immediately while in the second strategy, it chooses to propagate the delay to its subsequent activity. The result is that both projects can finish on schedule with the second strategy while a delay is introduced in P2 with the first strategy. So selecting an appropriate employee for the activity determines whether or not a feasible solution can be obtained. An immediate question is how to find an appropriate employee for a delayed activity. When all possible selections for all employees with same skills from all activities are linked together, a multi-fork tree is formed according to the data structure addressed in Ref. 19. Feasible solutions may exist in the tree which is detailed next.
4. ADAPTIVE ACO BASED STRATEGY FOR EMPLOYEE RESCHEDULING
In this section, first we provide an overview of the basic ACO algorithm. Then we present our adaptive ACO based strategy with three rescheduling rules defined to avoid unnecessary search for suitable employees for each delayed activity as much as possible.
4.1. An Overview of ACO Algorithm
Based on the above analysis, a feasible solution may exist in the multi-fork tree. How do we find the best feasible solution? One simple method is to traverse all possible paths in the tree. However, the number of nodes in the tree increases exponentially. Obviously this is an NP-hard problem. In this paper, we propose an adaptive ACO approach to solve such an optimization issue. But first, in this section, according to Ref. 20, we provide an overview of ACO developed by Dorigo et al. which has been widely applied to optimization problems. The key idea of ACO is the use of simulated pheromones, which attract ants to the better trails through graph, i.e. multi-fork tree in our case. The main processing loop alternates between updating the ant trails based on the current pheromone values and updating the pheromones based on the new ant trails. By sensing the concentration of pheromone at the path, other ants can choose appropriate path to find food. ACO algorithm works by dispatching a group of artificial ants to build solutions to the problem iteratively. In general, based on Ref. 20, ACO algorithm has two core procedures:
- (1)
Solution construction:
During each iteration of the algorithm, a group of ants sets out to build solutions to the problem. Each ant builds a solution in a constructive manner by selecting components step by step to form a complete solution. The selections are made according to pheromone and heuristic information.
In ACO, pheromone is a record of the past search experience of ants for guiding the following ants to make decisions. The selected component belonging to the best solutions found by the previous ants usually accumulates more pheromone, attracting more ants to select in future iterations. Heuristic provides some problem-dependent information that helps ants have higher probabilities to select appropriate component in the solution construction procedure.
- (2)
Pheromone management:
Along with the solution construction procedure, pheromone values are updated according to the performance of the solutions built by ants. Ants tend to deposit more pheromone to the components of better-performed solutions.
Our proposed solution is formed by ants selecting an appropriate employee for each delayed activity. In order to increase randomness of selecting employee, Roulette wheel selection from Ref. 21 is applied according to a random probability based on pheromone. The Roulette wheel is applied to choose a suitable employee. When a better feasible solution is found, the correspondent employee pheromone from the better solution at each activity will be strengthened while pheromones of other employees at each activity will be weakened. In our research, employee pheromone τ(ey → ax) is set to help ant select appropriate employee. τ(ey→ax) denotes that employee eY is selected to work on activity ax. The overall procedure of ACO is described below.
Step a:
Evaluate the value of τ(ey →ax) for all activities and initialize the number of generations and ants.
Step b:
Employee pheromone determines which employee is selected. τ(ey→ax) is used to compute the probability P(ey → ax). Then based on the Roulette wheel strategy, employee will be chosen. Here N is the set of all available employees.
Step c:
Given P1 is the delayed project that we try to reduce or even eliminate the delay, we define a fitness function that determines whether the ant finds a feasible solution. The fitness function is described as (Delay(P1)< min_delay(P1), finish time (P2) <= planned finish time (P2), ….., finish time (Pn) <= planned finish time (Pn) where min_delay(P1) indicates the minimum value of Delay(P1) when one ant finishes its tour.
Step d:
When all ants in one generation have finished the tour, the correspondent pheromones will be updated. If a feasible solution exists, at each delayed activity, the pheromones of the correspondent employees from the best-so-far solution will be strengthened while the pheromones of other employees are weakened.
Employee pheromone is changed as follows:
The evaporation is done by weakening pheromone trails.
Step e:
Increase the generation number by 1, when exceeding the maximum generation number set, the algorithm terminates with the final result as output, otherwise, go to Step b.
4.2. Proposed Rescheduling Strategy
In order to avoid unnecessary search as much as possible, we find that the selection for which employee to conduct the delayed activity can be optimized based on the following three rules. These rules form the foundation of our novel adaptive ACO strategy, which can increase its hit count, i.e. the number of feasible solutions found.
We assume that activity ain requiring skillx is a delayed activity. The original employee is ep. ej is the available employee who has skillx. Activity akm of project Pm is the next activity where employee ej will be working on. In order to express the rules clearly, we define some parameters in Table 4.
| employee_release_time | It is the time indicating that employee can execute new activity only after the employee has finished the current activity. |
| real_start_time | It is the maximum value of real finish time of all predecessors of the activity and the release time of the corresponding employee. The parameter indicates that activity is executed only after all predecessors of the activity have been finished and the corresponding employee is available. |
| late_start_time | It is the planned late start time of the activity. |
| finish_time (real_start_time,duration) | The function is defined to calculate real finish time of activity conducted by employee based on given real_start_time The detail of the function is given in the text below this table. |
| project_finish_time | It is the finish time of the project without any rescheduling. |
| project_earilest_possible_finish_time | It is the estimated earliest possible finish time of the project. |
Function finish_time(real_start_time,duration): from real_start_time, days are counted until given duration is satisfied. If the current day is weekend, the day will be skipped. The last day is the real finish time.
Explanation of parameters in rules
Rule 1:
If finish_time((ej→ain)(m1).real_start_time, (ej→ain). duration) > finish_time((ep→ain).real_start_time, (ep→ain).duration), employee ej cannot be rescheduled.
Explanation: If the finish time of activity ain with employee ej exceeds the finish time of activity ain with original employee ep, rescheduling should be avoided.
Rule 2:
If akm.late_start_time >= finish_time(ej→ain).real_start_time, (ej→ain).duration), rescheduling employee ej would not impact on the start time for activity akm.
Explanation: When employee ej is rescheduled to conduct activity ain, activity akm where employee ej will be working on needs to wait for finishing activity ain. If real_start_time of activity akm does not exceed its late start time, rescheduling would not impact on the start time for activity akm.
Rule 3:
When akm.late_start_time < finish_time(ej→ain).real_start_time, (ej→ain).duration), employee ejm cannot be rescheduled if Pm. project_earilest_possible_finish_time >Pm. project_finish_time.
Explanation: This rule has the opposite condition of Rule 2. When real_start_time of activity akm does exceed its late start time, we need to estimate the finish time of Pm. Each activity which has not been executed so far will be estimated based on its minimum duration in Pm. If the estimated finish time of Pm under this circumstance exceeds its planned finish time without any rescheduling, rescheduling should be avoided.
Now we describe the whole procedure of our generic rescheduling strategy based on adaptive ACO. The following steps show the flow of rescheduling strategy at each delayed activity.
Step 1: For the next activity, all employees with the required skills are assessed whether they conform to Rule 1. If there are no available employees, the activity will be executed by the original employee as scheduled. Otherwise all available employees are stored in array1.
Step 2: This step is to assess whether there exist any employees stored in array1 who conform to Rule 2. If so, all those employees are stored in array2. The end time of activity with each employee in array2 is calculated so that the employee with the minimum end time is chosen for rescheduling. Then go to Step 5. Otherwise, if there is no employee in array1 who conforms to Rule 2, go to Step 3.
Step 3: Employees stored in array1 will be assessed whether they conform to Rule 3. If there are no employees, the activity will be executed by the original employee, again as scheduled. Otherwise, those employees are stored in array3 and the original employee is also added to array3.
Step 4: One employee from array3 is chosen by antbased Roulette wheel selection based on employee pheromone.
Step 5: The activity is executed by the selected employee and the correspondent parameters such as real end time of the activity and release time of the employee are updated accordingly.
5. EVALUATION
In this section, we firstly set experiment parameters. Then five different experiments are reported to show the results of our strategy. Finally we compare our adaptive ACO with other two representative counterparts: basic ACO and GA. In addition, three real world software project instances are also utilized to evaluate our strategy. At the end, the threats to validity are presented.
5.1. Experimental Settings
In the reported experiments, we test the proposed rescheduling strategy when the number of concurrent projects is 2, 5, 10, 15, 20 respectively which are representative enough to demonstrate the overall performance of our novel strategy. We have also conducted experiments with other settings and the results are similar.
The project networks are derived from PSPLIB of Ref. 5 where the benchmark project networks in PSPLIB have been widely used in project management in various fields (including software project management). According to Ref. 22, these benchmark project networks are classical representation for the activity precedence relations of (software) projects. However, in order to appropriately capture the characteristics of real-world projects, we generate all parameters randomly for those networks. Randomized parameters include activity duration for employee and skill(s) of employee. Each project has 122 activities in this case.
We have conducted 5 different experiments for different number of concurrent projects in order to validate the effectiveness of our strategy. For each experiment, the strategy is run 10 times. In addition, in order to show the effectiveness of our strategy in larger scale projects, we choose project network with 122 activities. We assume that all 122 activities are different. So for one project, there are 122 required skills. The number of skills of each employee is 6 at most. The duration of each activity is set from 10 days to 25 days. Three levels of skills (high, medium and low) are set for employee randomly. So in order to show the effectiveness of our strategy, the original delay is set from 1 day to 70 days and is injected at the beginning of each project. The execution for experiments is based on Eclipse on a PC (Intel Core i7 CPU, 2.4GHz, 8GB RAM).
In addition to the above settings, in order to compare the three algorithms under the same iteration condition, we set the following parameters. The number of ants and generations of our adaptive ACO and basic ACO are set as 10 and 50 respectively so that the total iterations would be 500. Accordingly, the iterations of GA algorithms are also set as 50 and the population size of GA algorithm is set as 10.
5.2. Experiments
In Experiment 1, we have 2 concurrent projects. There are 244 different activities in total. Originally, delay occurs at one project. Our aim is that the delay at that project is reduced or even eliminated while the other project is not impacted. Table A.1 in Appendix shows the parameters and results of Experiment 1. Original delay is the value of injected delay. Remained delay is value of delay remaining after running. In Experiment 2, we have 5 concurrent projects. There are 610 difference activities in total. Similar to Experiment 1, delay occurs at one project, our aim is again that the delay at that project is reduced or even eliminated while all other projects are not impacted. Table A.2 in Appendix shows the parameters and results of Experiment 2. In Experiment 3, we have 10 concurrent projects. There are 1220 difference activities in total. Similarly, Table A.3 in Appendix shows the parameters and results of Experiment 3. In Experiment 4, we have 15 concurrent projects. There are 1830 difference activities in total. Table A.4 in Appendix shows the parameters and results of Experiment 4. In Experiment 5, we have 2concurrent projects. There are 2440 difference activities in total. Table A.5 in Appendix shows the parameters and results of Experiment 5.
5.3. Result Analysis
In order to show the effectiveness of our proposed strategy, we compare ours with other two representative approaches, namely basic ACO and GA algorithms.
Fig. 4 shows the overall hit count of the three strategies when the number of concurrent projects is 2, 5, 10, 15 and 20 respectively. The values are collected based on 10 runs for each strategy. From the figure, we find that the hit count of our adaptive ACO can be kept at a high value in all experiments while the hit counts of other two strategies are significantly lower. The average hit count of our adaptive ACO for 5 concurrent projects reaches 8.4. The hit counts of basic ACO and GA fall to 0 when the number of concurrent projects is from 5 to 20. In addition, combined with experiments presented in Section 5.2, we find that some relatively big delays can be reduced effectively in our adaptive ACO. For one example, in #5 of Experiment 4, the original delay is 47 days and the remained delay is reduced to 1 day only. However, in some scenarios with fewer employees, our proposed strategy probably fails to handle delays. For example, in #10 of Experiment 5, the original delay is 30 days and the remained delay is still 30 when the number of employee is 585. Experiment 5 has 2440 activities. Roughly each employee needs to conduct 4.1 activities on average. It indicates that many employees will be busy. So, it leads to fewer feasible employees for rescheduling. In general, our proposed strategy is effective in terms of finding a solution for reducing delays.

Comparison of overall hit count
Fig. 5 shows the hit count of eliminating delay for 10 runs among the three strategies. From the figure, we find only our adaptive ACO can obtain feasible solution in which delays can be eliminated. The average hit count of our adaptive ACO is about 1.8. In addition, combined with experiments presented in Section 5.2, we find that some relatively big delays can be eliminated in some experiments. For example, in #1 of Experiment 1, the original delay is 36 days which can be eliminated. It indicates that our proposed strategy can offer good quality of service for customers.

Comparison of hit count of eliminating delay
Fig. 6 shows the general effectiveness of our strategy. From the figure, we find that the delay of a project can be reduced to a much greater extent by our adaptive ACO with the average reduction degree nearly halved (about 46% on average) in comparison to others. It indicates that the delay can be handled much more effectively than other strategies as the reduction degrees of the others are normally well below 10%.

Comparison of degree of delay reduction
Fig. 7 shows the trend of delay reduction with given number of employees and number of skills when the number of concurrent projects is 2, 5, 10, 15 and 20 respectively. In order to learn the impact of number of employees and skills on delay reduction, we set five different numbers of employees and five different numbers of skills (6, 7, 8, 9, and 10) which employee can have at most. Experiments are carried out by fixing one parameter and changing another one. The degree of delay reduction is the average value after running 10 times. Here we need to emphasize that although after each run the total number of employees is different under the same group, the numbers fall to small interval, i.e. quite consistent. So the total number of employees can be averaged.

Trend of delay reduction with given number of employees and skills
From Fig. 7 (a), (b), (c), (d) and (e), we find that curves have a similar trend: (1) when the total number of employees is given, with the increase of the number of skills, the degree of delay reduction presents a upward trend; (2) when the number of skills is given, with the decrease of the total number of employees, the degree of delay reduction presents a downward trend. In essence, increasing of the number of skills or employees provides more available choices for rescheduling. So the degree of delay reduction also increases. In addition, some cases in Fig. 7 present opposite trend. For example in Fig. 7(a), when the number of skill is 7, the degree of delay reduction of 71 employees is slightly greater than that of 77 employees. The reason is that activity durations and delays are generated randomly for each run and the difference of employee numbers is not big between 71 employees and 77 employees. In addition, we also find that when the number of employee or skill is large, this trend is not obvious. The reason is that the more people can balance the lack of skills or the more skill can balance the lack of employees. But as a whole, the general trend meets our expectation.
5.4. Case Studies
In order to show the effectiveness of our research for the real world cases, 3 real instances which come from business software construction projects for a department store company are provided in Ref. 14. Since they only provide data for optimizing staffing scheduling at planning stage, we need to make some changes: (1) original delays are injected, (2) delay values are set from 1 to 70 days, and (3) in order to conform to the settings in our research, we regulate that one activity can only be conducted by one employee and employees are deployed randomly to conduct activities. According to the raw data, the number of employees is 30 and the number of activities is 45 in total. Each employee has 5 skills. For the case studies, we conduct 10 rounds of runs. Table 5 shows parameters and results of 3 real instances.
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 41 | 6 | 21 | 17 | 30 |
| #2 | 27 | 0 | 27 | 27 | 30 |
| #3 | 45 | 8 | 45 | 45 | 30 |
| #4 | 64 | 12 | 64 | 64 | 30 |
| #5 | 22 | 5 | 22 | 22 | 30 |
| #6 | 27 | 0 | 27 | 15 | 30 |
| #7 | 19 | 0 | 19 | 19 | 30 |
| #8 | 35 | 9 | 26 | 30 | 30 |
| #9 | 29 | 0 | 27 | 18 | 30 |
| #10 | 50 | 49 | 50 | 50 | 30 |
Parameters and results of 3 real instances
Fig. 8(a) shows hit count for our adaptive ACO, basic ACO and GA. The results are 10 out of 10, 3 out of 10 and 5 out of 10 respectively. Fig. 8(b) shows that only our adaptive ACO obtains solution in which delays are eliminated. Its hit count is 3 out of 10. Fig. 8(c) describes the reduction degree of the three strategies. The average reduction degrees of our adaptive ACO, basic ACO and GA are 75.2%, 8.6% and 14.4% respectively. According to Fig. 8, we find that no matter hit count or reduction degree, the effectiveness of our adaptive ACO is much better that of basic ACO and GA. Those results conform to our previous analysis. In addition, for our adaptive ACO, basic ACO and GA, compared with reduction degree of five groups’ experiments described in Section 5.3, reduction degree of 3 real instances is obviously higher. The main reason is that there are only 45 activities in 3 real instances in total. The smaller amount of activities narrows the searching space. In addition, there are sufficient staffs (30) with sufficient skills (5) in 3 real instances. So these factors lead to obtaining feasible solutions more easily. Finally experiments of the 3 real instances show the effectiveness of our proposed algorithm in the real word.

Comparison among three strategies at three real instances
In summary, our strategy is clearly much better than the other two approaches by producing quality feasible solutions. It is obvious that there are some deficiencies causing relatively lower hit count for the other two approaches: (1) in the basic ACO algorithm, the ant selects an employee only according to pheromone so that some feasible employees may be neglected as the reallocated employee may cause serious delay; (2) in the GA algorithm, one solution is generated based on crossover and mutation of previous solution, so for one activity, the current state of the activity cannot determine whether the activity needs to be rescheduled.
For example, although no any delay is introduced into one activity, the activity may need to be rescheduled. Finally, it is hard to find feasible solution.
Fig. 9 shows the running time for our rescheduling strategy when the number of projects is 2, 5, 10, 15, and 20 respectively, based on the average of 10 runs. When the number of projects becomes larger, the running time becomes longer as expected. However, since the time granularity of SPSP is relatively large which is normally in days, our strategy can finish rescheduling at tolerable time, namely from around 0.65 minutes up to 138.6 minutes for the experiments described in Section 5.2 on a single PC. In addition, the average running time of 10 runs for 3 real instances is around 0.27 minutes. Therefore, these experiments show that our proposed strategy is sufficiently efficient.

Trend of running time for 5 general experiments
5.5. Threats to Validity
Here we discuss the key threats to the validity of our evaluation.
Threats to External Validity. The main threat to the external validity of our evaluation is the representativeness of instances. Since most companies do not want to publish or record development process, it is hard to obtain real instances. So it threatens the external validity. To minimize this threat, the widely used PSPLIB set from Ref. 5 is applied in the paper. In order to fully simulate the real world, we generate all parameters such as duration, original delays etc. randomly based on project network from PSPLIB. In addition, in order to show the effectiveness of our research for the real world cases, three real world instances from Ref. 14 are also applied for validation of our strategy. Therefore, instances in this paper are reliable and can be true representation of real world software projects.
Threats to Internal Validity. The main threat to the internal validity of our evaluation is the comprehensiveness of our experiments. The result fluctuation is easily caused by the randomized data from PSPLIB in the experiments. It threatens the internal validity of our evaluation. To minimize this threat, we run each experiment for 10 times and the average values are collected. Average values can weaken deviation of calculation effectively. In addition, in order to validate the effectiveness of our strategy, instance which includes 122 activities is chosen from PSPLIB and 5 different experiments for different numbers of concurrent instances (2, 5, 10, 15, and 20) are conducted. We think that these provide sufficient comprehensiveness to demonstrate the effectiveness of our strategy.
6. CONCLUSION AND FUTURE WORK
In this paper, with a number of similar concurrent projects, we have discussed primarily on how to reduce or even eliminate the delay in a software development project without impacting on other projects. To achieve this goal, an innovative generic decision-making rescheduling strategy based on adaptive ant colony optimization has been proposed. More specifically, we provide three rescheduling rules in order to select appropriate employees across projects. The experiments have demonstrated that compared with other representative algorithms, our proposed strategy is much more effective to reduce or even eliminate the delay in an efficient manner.
The work presented in this paper focuses mainly on how to reschedule employees in order to reduce or even eliminate the delay. The proposed strategy can be deployed in a semi-automatic intelligent decision-support system for supporting project managers to handle the delay during software development. Therefore, our future work can be along this line.
7. ACKNOWLEDGEMENTS
This project is partly supported by the Australian Research Council Linkage Project (Grant LP0990393) and the National Natural Science Foundation of China (Grant No. 61402007 and No. 61300042) and the Jiangxi Engineering Laboratory on Radioactive Geoscience and Big Data Technology (Grant No. JELRGBDT201705).
Appendix
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 36 | 0 | 36 | 36 | 76 |
| #2 | 49 | 49 | 49 | 49 | 58 |
| #3 | 40 | 24 | 40 | 40 | 70 |
| #4 | 70 | 52 | 70 | 70 | 64 |
| #5 | 34 | 0 | 34 | 34 | 83 |
| #6 | 35 | 25 | 35 | 35 | 65 |
| #7 | 36 | 15 | 33 | 28 | 104 |
| #8 | 64 | 34 | 57 | 49 | 98 |
| #9 | 25 | 0 | 25 | 25 | 80 |
| #10 | 44 | 20 | 44 | 44 | 67 |
Parameters and results of Experiment 1
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 53 | 19 | 53 | 53 | 153 |
| #2 | 33 | 0 | 43 | 43 | 214 |
| #3 | 59 | 59 | 59 | 59 | 169 |
| #4 | 44 | 30 | 44 | 44 | 158 |
| #5 | 42 | 42 | 42 | 42 | 155 |
| #6 | 69 | 41 | 69 | 69 | 178 |
| #7 | 34 | 18 | 34 | 34 | 185 |
| #8 | 34 | 14 | 34 | 34 | 156 |
| #9 | 18 | 0 | 48 | 48 | 186 |
| #10 | 69 | 20 | 69 | 69 | 164 |
Parameters and results of Experiment 2
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 35 | 8 | 35 | 35 | 297 |
| #2 | 46 | 21 | 46 | 46 | 320 |
| #3 | 23 | 2 | 23 | 23 | 368 |
| #4 | 20 | 0 | 20 | 20 | 348 |
| #5 | 35 | 35 | 35 | 35 | 327 |
| #6 | 38 | 14 | 38 | 38 | 379 |
| #7 | 49 | 29 | 49 | 49 | 353 |
| #8 | 51 | 36 | 51 | 51 | 428 |
| #9 | 65 | 42 | 65 | 65 | 329 |
| #10 | 27 | 0 | 27 | 27 | 340 |
Parameters and results of Experiment 3
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 32 | 32 | 32 | 32 | 460 |
| #2 | 22 | 14 | 22 | 22 | 530 |
| #3 | 52 | 36 | 52 | 52 | 546 |
| #4 | 15 | 0 | 15 | 15 | 505 |
| #5 | 47 | 1 | 47 | 47 | 480 |
| #6 | 34 | 16 | 34 | 34 | 618 |
| #7 | 45 | 45 | 45 | 45 | 449 |
| #8 | 29 | 10 | 29 | 29 | 510 |
| #9 | 32 | 22 | 32 | 32 | 501 |
| #10 | 14 | 14 | 14 | 14 | 468 |
Parameters and results of Experiment 4
| Original delay | Remained delay | Number of employees | |||
|---|---|---|---|---|---|
| Adaptive ACO | Basic ACO | GA | |||
| #1 | 14 | 0 | 14 | 14 | 745 |
| #2 | 43 | 22 | 43 | 43 | 650 |
| #3 | 69 | 19 | 69 | 69 | 676 |
| #4 | 72 | 46 | 72 | 72 | 736 |
| #5 | 56 | 53 | 56 | 56 | 590 |
| #6 | 78 | 11 | 78 | 78 | 675 |
| #7 | 37 | 14 | 37 | 37 | 712 |
| #8 | 41 | 41 | 41 | 41 | 593 |
| #9 | 21 | 18 | 21 | 21 | 686 |
| #10 | 30 | 30 | 30 | 30 | 585 |
Parameters and results of Experiment 5
REFERENCES
Cite this article
TY - JOUR AU - Wei Zhang AU - Yun Yang AU - Xiao Liu AU - Cheng Zhang AU - Xuejun Li AU - Rongbin Xu AU - Futian Wang AU - Muhammad Ali Babar PY - 2018 DA - 2018/04/02 TI - Decision Support for Project Rescheduling to Reduce Software Development Delays based on Ant Colony Optimization JO - International Journal of Computational Intelligence Systems SP - 894 EP - 910 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.68 DO - 10.2991/ijcis.11.1.68 ID - Zhang2018 ER -
