An Improved Adaptive Genetic Algorithm for Solving 3-SAT Problems Based on Effective Restart and Greedy Strategy
- DOI
- 10.2991/ijcis.11.1.30How to use a DOI?
- Keywords
- genetic algorithm(GA); adaptive genetic algorithm(AGA); restart; greedy strategy; 3-SAT problems
- Abstract
An improved adaptive genetic algorithm is proposed for solving 3-SAT problems based on effective restart and greedy strategy in this paper. Several new characteristics of the algorithm are developed. According to the shortcomings of the adaptive genetic algorithm, it is easy to fall into the premature convergence and destroy optimal individual and make genetic performance decline. An improved adaptive genetic algorithm is proposed to adjust the crossover operator and mutation operator in different stages of evolution dynamically, and make use of the restart strategy to overcome the prematureness. At the same time, the algorithm adopts greedy strategy to make the maximum fitness value of each generation unabated, so as to accelerate the search for the optimal speed. In the experiment, several benchmark SAT problems in SATLIB are used to test the performance of the improved algorithm and the results are compared with those of other similar algorithms. The results show that the improved adaptive algorithm has a higher success ratio and faster solution speed.
- Copyright
- © 2018, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Satisability problem(SAT) which is the cornerstone of computational complexity theory, and a fundamental problem in many areas was the first NPC problem Contributions1. 3-SAT2–4 is the problem of determining whether all of a collection of 3-literal disjunctions (clauses) of Boolean variables are true for some truth assignment to the variables. 3-SAT is a special case of SAT which is the problem of determining whether all of a collection of clauses are true for some truth assignment to the variables contained in those clauses. So, algorithms for solving SAT problems can also be used to solve 3-SAT problems. 3-SAT problem is also a NPC problem. Any non-Deterministic Polynomial problem can be solved in the polynomial time to the SAT, so an algorithm that can solve the SAT problem efficiently is sure to solve all NP problems. In practice, there are a lot of NP problems, so it is of great significance to find an efficient and fast SAT algorithm and apply it to engineering practice, which can improve productivity and promote social development5,6. In the theoretical research SAT can be used for combinatorial optimization7, Real-time scheduling8,9, statistical physics10 and other basic issues; In industrial applications, SAT can also solve many problems, such as circuit verification11, chip design12, task scheduling, and other problems. SAT is of great use in electronic design automation13, equivalence checking14, bounded model checking15, and so on.
There are many optimization algorithms to solve the 3-SAT problems, which are divided into two categories: one is complete, the other is incomplete. The complete method adapts to the application class problem and the combination problem, such as DP16, MiniSat17 and Lingeling18, etc. The complete algorithm is theoretically guaranteed to find the solution, but since the SAT problem is an NP-complete problem, these algorithms are difficult to satisfy in terms of efficiency for solving 3-SAT problem. In the logical domain, restart is usually used by complete algorithms for solving the satisfiability problems. The restart refers to the termination of the algorithm and restarts during the operation of the algorithm, while the conflicting clauses learned still exists before restart. Before the restart, the information learned helps to adjust the global search order, which enhances the robustness of the algorithm. In this algorithm, the restart is used to overcome the premature problem19. In other fields, the application of restart strategy has also been widely developed20–21. Since the 1990s, the research hotspot of SAT problem has shifted to incomplete algorithm research. Although the incomplete algorithm cannot guarantee that it can find the solution, in most cases, the algorithm is faster than the complete algorithm and has high adaptability. The results of incomplete algorithms are very rich, mainly including local search algorithms and global search algorithms. Local search algorithms based on greedy strategies have been developed rapidly, such as GSAT23, WalkSAT24,25, Local Search26 and so on. Greedy strategy is through a series of search for the optimal solution to the problem. Every search is the best choice for a strategy in the current state. Although there are not many scholars in the field of 3-SAT search for recent years, they have gained rapid development and application in some other fields27–30, so greedy algorithm has certain application value and research significance. In incomplete algorithms for solving 3-SAT problems, genetic algorithm is the main algorithm with global search ability. The genetic algorithm for 3-SAT problem is a kind of important incomplete algorithm, Since 1989, there has been research in this area31–33, but generally speaking, the performance of the algorithm is not very good. Genetic algorithm research and a large number of experiments show that using heuristic information is an effective way to improve the performance of the algorithm. Therefore, It is critical to discover and utilize the structural information of the 3-SAT problem itself and the dynamic information in solving process.
Genetic Algorithm (GA), first developed by Holland34, is a global optimization probability search algorithm, which simulates the process of genetic evolution in the biological world. Compared with other optimization algorithms, it has many advantages, such as multi point search, parallel computing, scalability, robustness, and so on, so it has been extensively developed in theory35–38 and application39–42. It starts searching with the initial population which is any population, and by performing its unique genetic operations -- selection, crossover, and mutation operations, all the members are progressively searched into the increasingly good area of the solution space, until it satisfies the convergence criterion or the maximum number of iterations to be specified. In simple genetic algorithm(SGA), cross probability and mutation probability are empirical values and they are fixed and unchanged. It is generally believed that if the cross probability is too small, the population size is easy to fall into the local optimum because of the lack of diversity in the evolution process; If the crossover probability is too large, the diversity of the population is guaranteed, but when the latter reaches the best neighborhood, it will make it difficult for the individual to approach the best, which will greatly slow down the convergence rate of the population. In order to prevent the evolution of the middle of the stagnation, the algorithm set the mutation operator to increase the diversity of populations, but if we take fixed probability of variation, the population will gradually converge after many iterations, and “inbreeding” will develop, which will directly affect the performance of the offspring.
So M. Srinivas and L. M. Patnaik proposed an adaptive genetic algorithm(AGA)43, when the individual fitness is high, the crossover probability and mutation probability is reduced; when the fitness of the individual is low, the crossover probability and the mutation probability increase, that is to say, in each iteration, the crossover probability and the mutation probability are adaptively set according to the individual fitness value, which makes the adaptive genetic algorithm more efficient and global optimal. At present, many scholars have realized the advantages of dynamic adaptive technology and applied it in many fields44–47. However, as an optimization, adaptive genetic algorithm has some limitations, among which the biggest deficiency is premature convergence. Premature convergence means that when the algorithm has not yet searched for the global optimal solution, the offspring produced by the population can no longer surpass its parent, and the individual is almost no different from each other. Its main performance is in two aspects: each individual in the population stops evolving because of convergence; when the individual searches for the neighborhood of the optimal solution, it is always eliminated, making evolution linger. It is mainly because of the loss of diversity in the iterative process where the optimal solution has not yet been obtained. Premature convergence is a common phenomenon, which is unique to genetic algorithms. It is also the focus of genetic algorithm research. It is similar to the local extreme value problem, but the two are essentially different, because the "optimal solution" obtained in advance of the immature convergence is not necessarily a local extremum, and it has very strong randomness, so it is almost impossible to foresee whether it will happen. But in order to better study and apply the genetic algorithm, we must solve the problem of immature convergence, otherwise it will hinder the genetic algorithm to play the overall optimization ability and other excellent performance.
Aiming at the above shortcomings of adaptive genetic algorithm and combining the advantages of restart and greedy strategy, this paper proposes an improved adaptive genetic algorithm(I_AGA) for solving 3-SAT problem. At different stages of evolution, different adaptive crossover probabilities and mutation probabilities are set and reduce the blindness of the search process, while overcoming the premature problem through greedy and effective restart strategies. We carefully analyze the results of experiments using a series of benchmark instances, from which we can see that the proposed I_AGA obtains much better solving efficiency and success rate than the existing traditional genetic algorithms in latest and best-known database and improved genetic algorithms. We also perform experiments to compare the efficiency of improved adaptive genetic algorithms without restart. The results indicate that I_AGA is the most efficient algorithm among them.
This paper is organized as follows. Section 2 introduces the basic knowledge of 3-Satisfiability Problem and AGA for solving 3-SAT problem. Section 3 introduces that the proposed adaptive method is combined with greedy strategy and restart according to the properties of the optimal solution for each class of 3-SAT problems. In Section 4, the proposed approach is evaluated using several benchmark databases and compared with other similar algorithms. The paper is concluded in Section 5.
2. The 3-Satisfiability Problem and AGA for Solving 3-SAT Problem
2.1. Basic knowledge of 3-SAT problem
Before we give the solution of the 3-SAT problem, we first describe the general description and related symbols of the 3-SAT problem.
The symbol xi, i ∈ {1,2,…,n} in the text represents a boolean variable. Let Xn = {x1,x2,…, xn} symbolize a collection of boolean variables. The symbol l1, l2,… stands for literals. The symbol c1, c2,…, cm represents clauses. Let Cm = {c1, c2,…,cm} be a collection of clauses. Let F be CNF formula. Throughout this paper, n and m will represent the number of variable and that of the clauses of the input formula F. The value of boolean variable is either true or false. In the algorithm, 1 is true, and 0 is false in general. Value assignment defined on the variable set Xn is a function μ: Xn → {true, false}. Boolean variable xi or the negation of boolean variable ¬xi represents literal li, i ∈ {1,2,…, n}. A clause ci is made up of a disjunction of the some literals, ci = l1 ∨ l2 ∨… ∨ lk, and these k literals are different, and ci, which length is k, is a disjunction of k literals. A CNF means a conjunction of the some clauses. Here, it can be expressed by the form of F = c1 ∧ c2 ∧…∧ cm. If a SAT problem that its length of each clause cj, j = {1,2,…,m} is k, then means it is a k-SAT problem. In this paper, we just consider k = 3, meanwhile, we only concerned with the 3-SAT problem in which each clause consists of just 3 literals. The 3-SAT problem is a problem to study whether there exists an assignment of truth values to a set of Boolean variables that satisfy a conjunctive normal form formula to be true49.
2.2. Chromosome coding in AGA
When solving the 3-SAT problem by genetic algorithm, we must first encode the feasible solution of the problem into the corresponding string. In this paper, the true and false assignments of each variable in formula F is mapped into a coding of chromosomes, where length of a chromosome is the total number of variables, and the corresponding crossover method and design method are also designed. Eventually, a set of binary coded strings is obtained that makes the formula F satisfy the maximum number of clauses. Randomly take N such chromosomes as a population, that is, the size of the population is N.
2.3. Determination of fitness function in AGA
The fitness function is used to evaluate the individual, which is the only basis for the optimization process, and the fitness in the genetic algorithm is usually non negative. The fitness of individuals reflects the adaptability of individuals to the environment in order to survive. In the form of adaptive functions, the evolutionary behavior of the population will eventually be affected. The design of fitness function should be formulated according to different problems to be solved. In the optimization process of simple problems, the objective function can be directly converted into fitness function.
In this paper, we design that for a F formula, given a set of true and false assignments vi, and calculate the number of clause in F which is satisfied as fitness function for solving 3-SAT problem. That is, the fitness function expression is described as:
2.4 Adaptive probabilities of crossover and mutation in AGA
The adaptive crossover strategy pc and mutation strategy pm were proposed by Srinivas43:
The AGA algorithm makes pc, pm adjust themselves according to the current evolutionary state. To revent genetic algorithm from getting stuck at a local optimum, when
3. Improved Adaptive Genetic Algorithm
Genetic algorithm is the hope of a smooth search, and ultimately find a satisfactory solution or the optimal solution in ensuring the rich diversity of the premise, and It was not before that the population converges ahead of time and get a so-called "optimal solution" that is precocious and non-optimal. In this paper, an improved adaptive genetic algorithm is proposed to improve the above shortcomings of AGA. It is in the following arrears:
3.1. Selection strategy
The selection strategy is the operation of the survival of the fittest to the individual in the population, and determines the direction of the search. It is based on individual fitness as a measure of the standard, and chooses a relatively good individual as a father to breed the next generation. In order to reduce the divergence of the population optimum, replace the half of the worse population with half of the better population using selection strategy which differs from the selection strategy for standard genetic algorithm in selecting populations by selecting probabilities.
3.2. Adaptive crossover strategies and mutation strategies
In AGA, when population has converge to the global optimal,
When the generation of evolution g is less than or equal to 0.75 multiplied by the total generation G, that is g ≤ 0.75 * G ;
When g > 0.75 * G ;
In the early stage of evolution g ≤ 0.75 * G, the distribution of individuals is relatively scattered, and the proportion of excellent individuals is relatively small. At this time, the mechanism to prevent premature fall into the local optimum is adopted. When discriminant ratio
3.3. Greedy strategy
After selection, crossover and mutation, the algorithm begins to implement the following greedy strategy. It picks out the highest fitness individual in the contemporary population. If the individual with the highest fitness value satisfies the termination condition, the following greedy strategy is no longer executed. Otherwise, it picks a variable to make the difference between the fitness value subtracted before turning this variable and the fitness value after turning this variable minimize from all the variables in this chromosome. If the contemporary fitness value is greater than or equal to the previous generation fitness value and the fitness value after turning this variable is greater than the contemporary maximum fitness value, then turn the variable; if the contemporary fitness value is greater than or equal to the previous generation fitness value and the fitness value after turning this variable is less than or equal to the contemporary maximum fitness value, then the variance is not reversed; If the fitness value is smaller than the previous generation fitness value and the fitness value after the reversal of this variable is greater than the maximum fitness value of previous generation, then flip the variable; otherwise, replace an individual with the contemporary maximum fitness value with an individual of the previous generation with the greatest fitness value.
3.4. Improved adaptive genetic algorithm scheme
Compared with the general AGA algorithm, I_AGA algorithm adds the restart strategy and the greedy strategy, so the following Fig. 1 adds two judgments and an operation. I_AGA algorithm is shown in Fig.1, and the procedures of I_AGA algorithm are as follows.
|
I_AGA algorithm
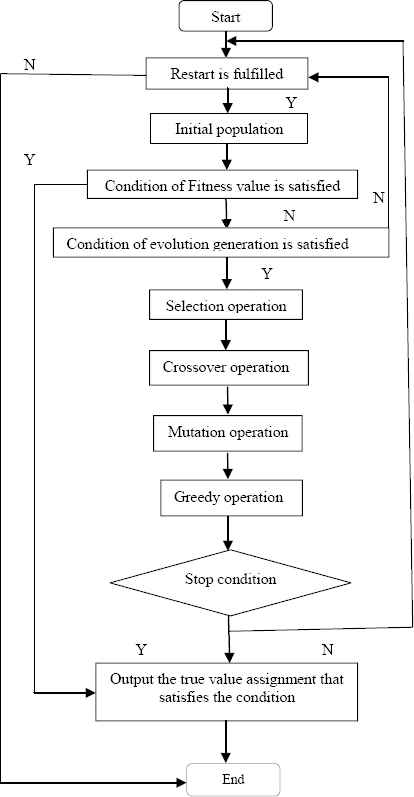
Flow chart of standard genetic algorithm
4. Experiments
To evaluate the performance of the proposed I_AGA, intensive computational experiments are carried out. In this section, the SATLIB benchmark problems are employed to test algorithms. The benchmark is available at www.cs.ubc.ca/~hoos/SATLIB/benchm.html . The problems in the SATLAB library have been widely used to test the performance of algorithms for solving SAT problem set. There are 3700 SAT problems in this problem set, and the ratio of the number of clauses and the numer of variables in these questions is about 4.3, which shows that the constraints of the SAT problem at this time are neither too many nor too few, and they belong to probabilities which are equal, so these problems are rather difficult to solve. According to the number of variables, the 3700 problems can be divided into 10 sets. Since scale of the last 600 questions is large, it takes a long time to find the optimal solution, so this article only tests the remaining 3100 problems which consists of 4 sets whose variables are 20, 50, 75, and 100 respectively. In addition to a set of 75 variables, the number of elements is 100, and the number of elements in the other three sets is 1000. In following experiments, the L represents string length, M represents the number of clauses. Most of the following algorithms are incorporated in a C program and implemented within Dev-C++5.11. We perform all experimental environment as: Processor (Intel(R) Core(TM)i5-3337 CPU@ 1.8GHz 2.7GHz), RAM (2.00GB), Operation system(Win7 64) bit.
If a run can find the optimal solution for the 3-SAT problem within the specified number of times and the number of restarts, the run is successful, otherwise it fails. The success rate S refers to the ratio of the number of questions that have been successfully found to the optimal problem and the total number of questions for the same type of problem. The repeated calculations of the experimental results are changing the string length L or algorithm at each run, and results are summed over 10000 runs, all running time limits are 200 seconds.
4.1. Compare to other algorithms
In order to show the effectiveness and efficiency, comparison between existing improved genetic algorithm HCGA in Ref. 31 and WAGA in Ref. 32 and the proposed I_AGA is carried out. Furthermore, we also compare the proposed I_AGA with the adaptive genetic algorithms in Ref. 43 and existing genetic algorithms fused by many effective ways in latest and best-known database48. Those similar algorithms based on genetic algorithm are tested with same parameters. In the following Table 1, for all classes of 3-SAT problems the number of population size P is 100 which is the same as the parameter settings in Ref. 31, and the limitations on the parameters generation are the same for every string length L in all algorithms. “-” means that none of the problems of solving these problem sets have been successful. The average time is used to calculate the mean time required to find the optimal solution of all the problems, that is to say, the problem of not finding the optimal solution is not involved in the calculation, and the best time is the fastest time to find the optimal solution in the current class of 3-SAT problem set. The generation size G setting is based on the performance of other algorithms.
| L | M | Algorithms | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| GA | WAGA | AGA | I_AGA | ||||||||||
| Time/s | S | Time/s | S | Time/s | S | Time/s | S | ||||||
| Average | Best | Average | Best | Average | Best | Average | Best | ||||||
| 20 | 91 | 0.261 | 0.049 | 0.931 | 0.010 | 0.001 | 0.874 | 0.002 | 0.001 | 0.022 | 0.162 | 0 | 0.999 |
| 50 | 218 | 0.355 | 0.114 | 0.432 | 0.411 | 0.032 | 0.579 | - | - | 0 | 2.460 | 0.014 | 0.998 |
| 75 | 325 | 1.533 | 0.334 | 0.280 | 2.445 | 0.378 | 0.280 | - | - | 0 | 23.85 | 0.080 | 0.970 |
| 100 | 430 | 9.766 | 2.039 | 0.118 | 6.858 | 0.960 | 0.132 | - | - | 0 | 65.02 | 0.571 | 0.349 |
The performance comparison of different algorithms for solving 3-SAT problem
Table 1 shows the comparison of the time and success rate of GA, AGA, WAGA and I_AGA algorithm for solving 3-SAT problems. The experimental results show that compared with the above thre algorithms, the performance of I_AGA algorithm is the best in terms of time and success rate. Among other algorithms, it has the highest success rate and the fastest time required for most problem sets. As the complexity of the problem increases gradually, the advantages of I_AGA are gradually obvious. Improved adaptive operator aimed at shortcomings of the adaptive genetic algorithm and the characteristics of the optimal solution of the 3-SAT problem is adapted to solving 3-SAT problem, and can effectively prevent premature convergence and the destruction of the optimal individual, so the performance of the success rate of I_AGA algorithm is obviously superior to AGA algorithm and GA algorithm. From Ref. 31, we know the experimental environment is clearly better than the experimental environment in this article, and I_AGA algorithm solving the 3-SAT problem L = 20, M = 91 needs less than 0.001 seconds, that is, close to 0 seconds. The algorithms of Table 2 and Fig. 2 are implemented within the experimental environment as: Processor(Intel (R) Core (TM)i5-3470 CPU @ 3.20GHz 3.200GHz), RAM (4.00 GB),Operation system(Win7 64) bit from Ref. 31., where SGA is Standard Genetic Algorithm, and GSAT is a local search based on greedy strategy. The experimental environment in Ref. 31 is clearly better than the experimental environment in this article. However, the success rate of HCGA algorithm is obviously smaller than that of I_AGA algorithm. Moreover, the time required for solving is significantly higher than that of the I_AGA algorithm, so I_AGA algorithm is superior to HCGA algorithm.

The relationships between success probability S and string length L.
| L | M | SGA/s | GSAT/s | HCGA/s |
|---|---|---|---|---|
| 20 | 91 | 1.034 | 0.356 | 0.256 |
| 50 | 218 | 687.7 | 50.62 | 38.09 |
| 75 | 325 | - | 2420 | 128.8 |
| 100 | 430 | - | - | 85714 |
The time comparison of difference algorithm for solving the 3-SAT problem
For any improved genetic algorithm, there are two parameters of population number and the number of generation. As the parameters vary, the performance of the algorithms varies considerably. In order to describe the algorithm in more detail, how will the performance of the algorithm and other algorithms vary with the parameters? Then we use two diagrams to more intuitively describe the performance difference of the different algorithms as one of the parameters changes in Fig. 2 and Fig. 3. G_AGA algorithm is I_AGA algorithm without the restart methods.

The change curve of success rate of different algorithms with different constraints of generation and P=100, L=75. The horizontal axis represents generation size and the vertical axis represents the success rate.
Fig. 3 shows the different success rate for above algorithms with different restrictions of generation and L=75, P=100. Under different restrictions of generation, the success rate of the AGA algorithm is almost 0, so it is not represented in the figure. As can be clearly seen from above Fig. 3, the I_AGA algorithm is better than other algorithms even if the restart strategy is not used. That is to say, the performance of the G_AGA algorithm is obviously superior to other algorithms.
Fig. 4 shows the different success rate for above algorithms with different restrictions of population and L=75, G=1000. Under different restrictions of population, the success rate of the AGA algorithm is almost 0, so it is not represented in the figure. When P = 50, the success rate of I_AGA is 1 and the average time is 7.461, and the performance of I_AGA algorithm is better than that of the one in the Table 1. As can be clearly seen from above Fig. 3 and Fig. 4, whatever the two parameters of generation and population change, the performance of I_AGA algorithm is the best in these algorithms, and the success rate of all algorithms increases with the increase of the generation parameter value, and fluctuates with the increase of the population parameter value, that is, the optimal range of the population parameter value exists for all algorithms. The curve trend of I_AGA algorithm and G_AGA algorithm is roughly the same, and it can be seen that when the range of population is 20 ~ 100, the performance of improved adaptive genetic algorithm is better. Even if the I_AGA algorithm does not use the restart strategy, the maximum success rate of G_AGA is far greater than the maximum success rate of other algorithms.

The change curve of success rate of different algorithms with different constraints of population size and G=1000, L=75. The horizontal axis represents population and the vertical axis represents the success rate.
4.2. Comparison of different parameters in I_AGA algorithm
For different parameter settings, the performance of the algorithm is different, so it is very important for any algorithm to find the appropriate parameter settings. In addition to the two parameters of population and generation, this algorithm also has an important restart parameter. In order to get a better parameter range, we can see that when G = 1000, P = 50, the performance of this algorithm is better, so, in order to get a better restart parameter interval, when P = 50, different parameters of the restart change with different generation parameters, we get different success rate changes curve in the following Fig. 5; When G = 1000, different parameters of the restart change with different population parameters, and we get different success rate curves in the following Fig. 6. In the below figure, R represents the number of restart.

The change curve of success rate of different restart with different constraints of generation size and P=50, L=75.

The change curve of success rate of different restart with different constraints of population size and G=1000, L=75.
It can be seen from the following Fig. 5 that the trend of all curves is up with the increase of the generation parameter value, and when R is greater than 50, G=1000, the corresponding success rate for the R of the different curves is 1. So when P = 50, L =75, the optimal interval for the restart parameter is 100 ~ 200 and optimal interval for the generation is 800 ~ 1000.
As can be seen from Fig. 6, the three curves for R = 100, 150, 200 are almost coincident, and as the population parameter changes, the shape of all curves is approximately the same, that is, all curves have similar optimal intervals of population parameter. From the difference between the R=0 curve and the R>0 curves in Fig. 4 and Fig. 6, we can see restart strategy is important to I_AGA algorithm. And when [20,60] P ∈, R ∈ [100,200], the corresponding success rate for the R of the different curves is 1. So when L = 75, G = 1000, the optimal interval for the restart parameter is 100 ~ 200, the optimal interval for the population parameter is 20 ~ 60. From the above Fig. 5 and Fig. 6 if there is no time limit, the greater the value of the restart parameter is, the better the performance of the algorithm is, and the greater the value of the generation parameter is, the better the performance of the algorithm is. Therefore, combined with Fig. 5 and Fig. 6, restart parameter, population parameter and generation parameter of the optimal interval is [100, +∞ ), [20,60], [800,+∞ ), when L=75, where they all take integers. Next, we let R=200, P=50, and generation parameter values be the same as those in Table 1, with the change of the various 3-SAT problems, then we get the performance Table 3 under the parameter values that are suitable for I_AGA algorithm.
| L | S | Time/s | Average | ||
|---|---|---|---|---|---|
| Average | Best | R | G | ||
| 20 | 1 | 0.260 | 0 | 3.627 | 62.84 |
| 50 | 0.999 | 0.924 | 0 | 0.603 | 517.6 |
| 75 | 1 | 7.330 | 0.062 | 1.220 | 1655 |
| 100 | 0.938 | 22.58 | 0.047 | 1.945 | 3246 |
Experimental results of I_AGA algorithm after adjusting parameters for SATLAB
In the above Table 3, The average R is used to calculate the mean number of restart required to find all the problems of the optimal solution, and The average G is used to calculate the mean evolutionary generation required to find all the problems of the optimal solution. In fact, R is multiplied by G to represent the evolutionary generation of the algorithm. As you can see from Table 3, the performance of the I_AGA algorithm after the improvement of parameters is obviously better than that of Table 1. Especially when L=100, I_AGA algorithm improves the success rate of about 2.7 times, and the average time was reduced by about 2.9 times. When L=20 and L=75, success rate of I_AGA algorithm reached 1, it shows that I_AGA algorithm has better search ability and can jump out of local optimal solution to get rid of premature convergence, so making the performance of the algorithm is better than other comparative algorithms.
5. Conclusions
Aiming at the 3-SAT problem, an improved adaptive genetic algorithm is proposed. The I_AGA algorithm takes into account both the overall control of the system when the immature convergence occurs, and the regulation of each individual when the immature convergence is not taken into account to set up the adaptive crossover probability and adaptive mutation probability, and combined with restart strategy and the greedy strategy, which will not only prevent the algorithm from premature convergence in advance without obtaining the optimal solution, but also speed up the search. In the experiment, a large number of standard SAT problems were used to test the performance of the algorithm. The Experimental results show that the I_AGA algorithm can effectively improve the AGA algorithm and GA algorithm on the immature convergence problem, and show better global convergence. Compared with other genetic algorithms in the literature, the I_AGA algorithm has higher success rate and faster solution speed.
How to overcome the immature convergence is one of the most prominent problems of genetic algorithm for 3-SAT problems. If we want to solve the problem fundamentally, we still need to discover and research. Further research is needed to explore the effect of different 3-SAT problems on adaptive crossover probability and mutation probability. We only consider the effect of the optimal solution of 3-SAT problem on the adaptive probability, but in fact, the larger 3-SAT problem is very complex. We will consider other influencing factors in the future for more complex data sets for testing.
Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No.61673320) and the Fundamental Research Funds for the Central Universities (Grant No.2682017ZT12, 2682016CX119). The authors also gratefully acknowledge the helpful comments and suggestions of the teachers and students who come from System Credibility Automatic Verification Engineering Lab of Sichuan Province of Southwest Jiao tong University in China, which have improved the presentation.
Reference
Cite this article
TY - JOUR AU - Huimin Fu AU - Yang Xu AU - Guanfeng Wu AU - Hairui Jia AU - Wuyang Zhang AU - Rong Hu PY - 2018 DA - 2018/01/01 TI - An Improved Adaptive Genetic Algorithm for Solving 3-SAT Problems Based on Effective Restart and Greedy Strategy JO - International Journal of Computational Intelligence Systems SP - 402 EP - 413 VL - 11 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.11.1.30 DO - 10.2991/ijcis.11.1.30 ID - Fu2018 ER -
