International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 10, Issue 1, 2017, Pages 1082 - 1101

Novel search space updating heuristics-based genetic algorithm for optimizing medium-scale airline crew pairing problems

Authors
Nihan Çetin Demirelnihan@yildiz.edu.tr, Muhammet Devecimuhammetdeveci@gmail.com
Department of Industrial Engineering, University of Yildiz Technical, Barbaros Bulvarı 34349 Yildiz, Istanbul, Turkey
Received 27 April 2017, Accepted 5 July 2017, Available Online 20 July 2017.
DOI
10.2991/ijcis.2017.10.1.72How to use a DOI?
Keywords
Airline crew scheduling; Crew pairing; Set-covering; Genetic algorithm; Heuristics
Abstract

This study examines the crew pairing problem, which is one of the most comprehensive problems encountered in airline planning, to generate a set of crew pairings that has minimal cost, covers all flight legs and fulfils legal criteria. In addition, this study examines current research related to crew pairing optimization. The contribution of this study is developing heuristics based on an improved dynamic-based genetic algorithm, a deadhead-minimizing pairing search and a partial solution approach (less-costly alternative pairing search). This study proposes genetic algorithm variants and a memetic algorithm approach. In addition, computational results based on real-world data from a local airline company in Turkey are presented. The results demonstrate that the proposed approach can successfully handle medium sets of crew pairings and generate higher-quality solutions than previous methods.

Copyright
© 2017, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

1. Introduction

Airline companies have used operations research techniques to solve planning and scheduling problems since 1950 [1]. These techniques greatly impact planning and managing the operations of airlines. Advances in computer technology and optimization models have allowed more complex issues to be addressed and overcome; thus, airline-related problems can be solved in a shorter period of time. These models have saved millions of dollars, and many airline companies have established operations research departments [2].

Planning and operational problems are the most common issues encountered by airline companies. Each problem has its own characteristics and objectives. Airline crew scheduling is among the major planning problems referred to frequently in the literature. Crew expenses are the second largest expense for airlines after the cost of fuel. Because fuel costs cannot be reduced, effective and economical crew scheduling is highly valued by airline companies. Because staff costs are the largest expense that can be controlled by airline companies, scheduling cabin crew members in the most efficient manner is of utmost importance for airline planning [3]. Given its economic aspect and huge impact on operations, airline crew scheduling, which is comprehensive in nature, is an NP-hard optimization problem that must be solved under numerous constraints. The economic significance and complexity of this problem has attracted the attention of the operations research community in recent years. To facilitate a solution to this problem, various exact and meta-heuristics-based methods have been developed [4–12].

Because of its cumbersome nature, airline crew scheduling has been divided into two consecutive stages: crew pairing and crew rostering. The main objective of the crew pairing process is to find the pairings with minimum cost that cover all flights within legal rules. Crew rostering (or crew assignments) is conducted for all legal pairings generated in the previous stage [13]. This study analyses the crew pairing problem. The inputs of the crew pairing problem are the flight legs included in the airline’s timetable. Considering the scope of the crew pairing process in real life, it is not possible to generate all crew pairings (which is acceptable for large airlines). Additionally, generating a large quantity of crew pairings would make the optimization phase more difficult. Most of the studies in the literature have solved the problem by generating as few crew pairings as possible [14, 9].

In this study, a dynamic-based genetic algorithm is proposed for medium-scale scheduling problems. The objective is to find a set of minimum-cost crew pairings that meets the demand for each flight leg in the airline’s timetable within all legal limits. The major differences between our study and previous genetic algorithm studies are as follows:

1) A genetic algorithm has been developed to solve medium-scale crew pairing problems. 2) Previous studies considered a particular element of the generated crew pairings and excluded the rest from the solution set, whereas in our study, all legal pairings are generated and their subsets are considered. 3) The length of the chromosome representing a solution changes dynamically in each iteration. Thus, the chromosome length varies during the optimization run. 4) Our study also has multi-objective characteristics because we represent penalty values for more than one KPI (key performance indicator) in the objective function. The high cost of crew pairing and the number of deadheads have been minimized. For these problems, new heuristic algorithms have been developed.

The rest of this paper is organized as follows. Section 2 provides an overview of the background and describes the airline crew pairing problem. Section 3 explains the proposed evolutionary algorithms. Section 4 presents a case study from Turkey and compares the performances of different evolutionary algorithms applied to this case study, and it also describes the experimental results and analyses. Finally, Section 5 presents the conclusions.

2. Background

2.1. Crew pairing

Studies on airline crew pairing have used the set-covering and set-partitioning models. Information on studies that have solved airline crew scheduling problems by exact, approximate or meta-heuristic methods is given in Tables 1 and 2.

Author (Year) Fleet Assignment Aircraft Routing Crew Pairing Crew Rostering Problem Type Application Flight Data Data Access Airline/Country SC /SP Solution Methods
Lavoie et al. [15] - - x - 2 Weekly Real up to 329 Private Air France SC Column generation, generalized linear programming and shortest path
Levine [16] - - x - - Real - Private - SP Hybrid genetic algorithms
Chu et al. [17] - - x - Daily Real - Private American Airlines - Zero-one integer program
Desaulniers et al. [18] - - x - Weekly Real between 154 and approximately 1200 Private Air France SP Nonlinear IP and Dantzig-Wolfe decomposition
Merle et al. [19] - - x - - Real 986 Private - SP Linear programing, column generation
Yan and Chang [20] - - - x Weekly Real - Private Taiwan airline SP Shortest path problem and column generation
Mercier et al. [21] - x x - Daily Real up to 700 Private - - Benders decomposition and column generation
Zeghal and Minoux [22] - - - x Monthly Real - Private TunisAir - Integer linear program
Medard and Sawhney [23] - - x x - Real - Private - SC/SP Column generation
Mercier and Soumis [24] - x x - Daily Real up to 500 Private - - Benders decomposition, column generation
AhmadBeygi et al. [25] - - x - Weekly Real 329 Private U.S Airlines SP Column generation and integer programming
Papadakos [26] x x x - Daily and Weekly Real 372 and over 2100 Private European and North American airlines SP Enhanced Benders decomposition and accelerated column generation
Deng and Lin [8] - - x - Daily Real (Ozdemir & Mohan, 2001) - Private - - Ant colony optimization and swarm intelligence
Ionescua and Kliewer [27] - - x - Daily Real 396-427 Private European Airline SP Column generation
Saddoune et al. [28] - - x x Daily, Weekly and Monthly Real between 1011 and 7527 Private North American Airline SP Column generation and bi-dynamic constraint aggregation
Duck et al. [29] - x x - - Random generated - Private - SP Column generation and Dynamic programming
Aydemir-Karadag et al. [11] - - x - Daily Random generated 100 and 200 Private - SC Column generation, genetic algorithm
Azadeh et al. [10] - - x - Daily Random generated 25, 50, 100 and 150 Private - - Particle swarm optimization, genetic algorithm and ant colony optimization
Cacchiani and Salazar-González [30] x x x - Daily Real 100-150 Private - - LP-relaxation by column generation

SC: Set covering, SP: Set partitioning.

Table 1.

Overview of previous studies that used meta-heuristics and matheuristics for the airline crew scheduling problem.

Author (Year) Fleet Assignment Aircraft Routing Crew Pairing Crew Rostering Problem Type Application Flight Data Data Access Airline/Country SC /SP Solution Methods
Muter et al. [31] - - x - Daily and Weekly Real 96, 135, 490 Private Turkey SC Row and column generation and multi-label shortest path
Saddoune et al. [32] - - x - Daily, Weekly and Monthly Real between 1011 and 7527 Private North American Airline - Column generation
Salazar-González [33] x x x x - Real between 100 and 150 Private Binter Canarias S.A - Integer programming and mixed integer linear programming
Zeren and Ozkol [13] x Monthly Real between 15656 and 17318 Private Turkish Airlines SC Integer programming, Column generation and heuristics
Chen and Chou [34] - - - x - Real - Private - - Genetic algorithms
Kasirzadeh et al. [35] - - x x - Real - Private US carrier SC Column generation
Quesnel et al. [36] - - x - Monthly Real Between 271 and 479, and also from 1463 to 1987. Private North American Airline SP Column generation
Yildiz et al. [37] - - x - Weekly Real 378 and 470 Private - SC Column generation
Table 2.

Continue.

In most airline crew scheduling research, matheuristic studies are performed that utilize both heuristic and exact approaches. We can define matheuristics as optimization algorithms generated by the interoperation of meta-heuristics and mathematical programming methods. Column generation and integer programming (heuristic branch-and-bound) are the most commonly used methods.

2.2. Memetic algorithm

A memetic algorithm (MA) is a heuristic algorithm that uses local search (LS) techniques and is a genetic algorithm and hybrid-structured evolutionary algorithm (EA). MAs are enhanced population-based EAs that were first developed by Moscato [38] to solve discrete optimization problems. The main components of MAs are crossover, mutation and hill climbing [39]. LS algorithms attempt to improve the current solution. Within MAs, hill climbing, tabu search and simulated annealing are used as LS algorithms. MAs are used to solve NP-hard problems by combining genetic algorithms (GAs) and LS techniques [40].

Our ultimate objective is to develop a GA that can handle medium data sets in an effective manner and generate outcomes that are of high quality.

2.3. Related works

Because current approaches are not sufficient for solving large-scale problems, most studies apply integrated heuristics with these approaches. Several studies have been performed on the application of GAs based on meta-heuristics to the airline crew scheduling problem in the literature. In these studies, the set-partitioning (SP) problem or set-covering (SC) problem is generally considered to solve the crew pairing optimization problem. Both problems have been shown to be NP-complete [41].

In Zeren and Ozkol’s study [9] of 700 flights, Ozdemir and Mohan’s study [42] of 300 flights, Kornilakis and Stamatopoulos’s study [14] of 2100 flights, Chang’s study [43] of 700 flights and Sou and Teghem’s study [7] of 631 flights, the results were generated without using all pairs. However, in this study, all pairs are produced, and by updating the solution space dynamically, the GA yields better solutions in big column numbers.

Using the dynamic approach proposed in this paper, we were able to generate solutions that are of better quality using much larger data sets than those used in studies that include GAs. An overview of previous work on relevant GA studies is provided in Table 3.

Author (Year) Crew Pairing Crew Rostering Problem Type Application Flight Data Data Access Airline/Country Formulation
Beasley and Chu [44] x - - Random generated - Private - SC
Levine [16] x - - Real - Private - SP
Ozdemir and Mohan [42] x - Daily Real - Private - -
Kerati et al. [45] - x - - - Private - -
Kornilakis and Stamatopoulos [14] x - Monthly Real 2100 Private Olympic Airways SC
Chang [43] x x Weekly Real about 700 Private Taiwan -
Souai and Teghem [7] x x Daily Real up to 631 Private - SP
Zeren and Ozkol [9] x - Monthly Real 714 Private Turkish Airlines SC
Azadeh et al. [10] x - Daily Random generated 25, 50, 100 and 150 Private - -
Table 3.

Overview of previous studies that used genetic algorithms for the airline crew scheduling problem.

2.4. Fundamental definitions and rules

Crew pairing problems attempt to determine the crew pairing with minimum costs that would meet the needs of each flight leg on the schedule. The airline timetable is used as an input at this stage. Then, duties and pairings are generated according to the rules laid down by the airline companies, the Directorate General of Civil Aviation (DGCA) and the Federal Aviation Administration (FAA). Fig. 1 shows the duties and crew pairings generated in line with the flight legs used in the airline’s timetable. The following definitions are used to address the crew pairing problem [3]:

  • Flight (flight leg or leg): Period between aircraft (AC) take off and AC landing.

  • Duty: Period comprising one or more flight legs, including the briefing time, which is the preparation period for the duty, and the debriefing time, which is the preparation period of the AC for the next flight crew.

  • Crew pairing: Period comprising one or more duties. Crew pairings also include the rest periods between duties.

Fig. 1.

Example of a crew pairing with an IST airport as the crew base.

The limits that must be respected to ensure that a duty or crew pairing is legal consist of a rest period, connection time, flight time and duty time. Connection times for a duty period must be within a certain range (minimum and maximum). The total flight time refers to the time spent in a duty period, the block time refers to the flight time during a duty, and the number of flight legs must not exceed the given ranges. A certain period is also allocated for briefing before each duty period and debriefing at the end of each duty period. The rules applied for crew pairing vary according to airlines and countries. The rules for the crew pairing problem can be found in [46].

  • Connection time: A connection during duty is called a sit connection time, which is the time between two consecutive flight legs in a duty. Generally, airlines consider minimum and maximum sit connection times, which are usually between 30 min and 3 h (sometimes 4 h).

  • Rest: A connection between two duty periods is called a rest, layover or overnight connection.

  • Brief: The elapsed time before the first leg of the duty.

  • Debrief: The elapsed time after the last leg of the duty.

  • Deadhead: If a crew member flies as a passenger rather than as a cockpit or cabin attendant, this flight is regarded as a deadhead flight for that crew member. Deadhead flights should be minimized because they reduce the passenger transport capacity and the crew utilization efficiency [13].

3. Proposed Methodologies

In this study, we propose a fast, strong and dynamic-based GA approach for airline crew pairing. The algorithm’s main logic provides a sub-optimal solution for medium-scale problems by solving them in small subsets. The proposed method uses a small subset of the problem that continuously repeats itself in line with the information obtained from the GA solution. The pairings that worsen the solution in the subset and the pairings that improve the solution in the main set are continuously replaced to develop updated heuristics.

The proposed methodology consists of five stages. (1) All legal crew pairings are generated (pairsAll). (2) A subset is formed by randomly (knowledge-based random) choosing pairings from the generated crew pairings, including all flights (select the initial from pairsAll). (3) The steps of the GA are applied to optimize the problem. (4) After the GA produces a certain iteration, the population’s best chromosome and pairings of this chromosome are kept in memory for the next round. Then, the loop returns to stage 3, and the pairings that will improve the solution (low-cost) in the main set are searched instead of the pairings that will worsen the solution (high-cost) in the subset. In addition, the other developed heuristics algorithm and alternative pairings that will produce the fewest deadheads for each flight are searched. (5) The best crew-paring solution set is obtained by continuously executing procedure stages 3 and 4 until the loop ends. The schematic diagram of the proposed methodology for the crew pairing problem is shown in Fig. 2.

Fig. 2.

Stages of the proposed dynamic-based GA methodology.

3.1. Crew pairing generation

The aim of this stage is to obtain a set of all legal crew pairings. The crew pairing generation method consists of two stages: (1) duty generation and (2) pairing generation. In the first stage, all legal duties are generated using the set of flights (see Section 2.4). A depth-first search algorithm is employed for duty generation. In the second stage, crew pairings are generated from flight duties with a similar algorithm (depth-first search algorithm) after duty generation. This algorithm searches in the space of all possible subsets of all flight legs [14].

  1. 1

      Procedure GeneratePairings (pairList)

  2. 2

        currentPair = create an empty pair;

  3. 3

        for each duty do

  4. 4

          if duty starts from homebase

  5. 5

            Insert duty to currentPair;

  6. 6

            SearchForPairings (currentPair, pairList)

  7. 7

            Remove duty from currentPair;

  8. 8

      Procedure SearchForPairings (currentPair, pairList)

  9. 9

        for each duty (that starts from the arrival station of currentPair arrives) do

  10. 10

          Insert duty to currentPair;

  11. 11

          if currentPair is valid (whether ends at the same homebase city)

  12. 12

            Insert currentPair to pairList;

  13. 13

          if currentPair can have more duties

  14. 14

            SearchForPairings (currentPair, pairList);

  15. 15

          Remove duty from currentPair;
Algorithm 1

Pseudocode of the pair generation

The GeneratePairings method is a recursive procedure that allows us to search for duty connections that form all possible crew pairings. In the first phase, all duties are reviewed in the main procedure. For duties starting from the homebase, the procedure is executed to search for possible duties that can be added to the pairing. The steps of this process are shown between lines 2 and 7. In the second phase, however, duties finishing at the homebase sub-procedure are executed to search for possible duties that can be added to the pairing. Any suitable duties are searched for in lines 9 and 10 and added to the currentPair. In lines 11 and 12, the generated pairing is added to the pairList if applicable. In lines 13 and 14, if the length of the current pairing allows us to add more duties, then recursive procedure reruns in the search space. The pairList is the list of all valid pairings created by the recursive code.

For an airline crew pairing problem that consists of f flights, d duties and p pairings of duties, the cost function of the CPP (crew pairing problem) can be defined as follows:

The total duty duration is used as the duty cost in the code and can be formulated as given in Eq. (1):

Duty cost=Min(Cjduty)=∑i=1faij(Ciflight+∑l=1faljuilCilconnectionTime)∀j=1,2 … ,d

The first and second part of the duty cost equation can be defined as follows:

  1. (1)

    Required pay for each flight in each duty and

  2. (2)

    Connection time between flights.

The first and second part of the pairing cost equation can be defined as in Eq. (2):

  1. (1)

    Required pay for each duty in each pairing (duty cost) and

  2. (2)

    Connection time expenses between duties (hotel cost).

Pairing cost=Min(Ckpair)=∑j=1dbjk(Cjduty+∑q=1dbqkhjqCjqrestPeriod)∀k=1,2,…,p

The elapsed time includes a briefing period before the first leg of the duty and a debriefing period after the last leg of the duty.

i

=1,2,….f (f Є F: set of all flight legs)

j

=1,2,…,d (d Є D: set of all legal duties)

k

=1,2,…,p (p Є P: set of all legal pairings)
Notation Define
Cjduty The basic payment for a duty j.
Ciflight The cost of each flight i.
Cilconnection Time The connection time cost between two consecutive flights i and l.
CjqrestPeriod The rest time cost between two consecutive duties j and q.
aij If flight i is covered by duty j, aij = 1; otherwise, aij = 0.
alj If flight l is covered by duty j, alj = 1; otherwise, alj = 0.
uil If flight i follow flight l, uil = 1; otherwise, uil = 0.
bjk If duty “j” is covered by pairing k, bjk = 1; otherwise, bjk = 0.
bqk If duty “q” is covered by pairing k, bqk = 1; otherwise, bqk = 0.
hjq If duty j follows duty q, hjq = 1; otherwise, hjq = 0.
Table 4.

Mathematical notation of crew pairings.

  1. 1

      Procedure InitializeActivePairs (Flights, pairsAll, pairsActive, maxStep)

  2. 2

        initialize step = 0

  3. 3

        While (step < maxStep)

  4. 4

          initialize temporaryFlights = Flights

  5. 5

          initialize coveredFlightList = {}

  6. 6

          While (temporaryFlights.length > 0)

  7. 7

            select a random flight Fi out of temporaryFlights.

  8. 8

            if (Fi has not been included by coveredFlightList yet)

  9. 9

            find the "crew pairing list" PL that includes pairings that cover Fi with minimum deadheading (by checking coveredFlightList) out of pairsAll.

  10. 10

              select a random pairing P out of PL and Insert P to pairsActive.

  11. 11

              add all flights of P to coveredFlightList.

  12. 12

            remove Fi from temporaryFlights.

  13. 13

          step++
Algorithm 2

Pseudocode of the initial subset

3.2. Initial pairing (subset) selection with heuristic solution

Unlike other studies, this study generates a knowledge-based random subset \to cover all flights among all generated pairings, and then this subset continues to renew itself. A heuristics approach is developed below for generating the initial subset.

3.3. Set covering master model for optimization

Selecting the set with the best crew pairing is modelled as an SC or SP problem in the literature. The SC model is used in this study because there is a clear analogy between the SC model and the crew pairing problem. In this model, each row represents a flight in the airline time table, and each column represents a generated crew pairing. In addition, F represents the flight set, and P represents the legal pairings created by these flights. The SC problem for the crew pairing problem can be defined as follows [6, 13]:

The SC model perfectly fits and provides all the representation needs of the crew pairing problem.

Set covering:

Min(z)=∑j=1pcj*xj

Which is subject to

∑j=1paij*xj≥1∀i∈F
xj∈{0,1} ∀j∈Pxj={10if pairing j is selected;otherwiseaij={10if flight leg i is covered by pairing j;otherwise

Eq. (3) shows the objective function in which the total cost is calculated. Eq. (4) indicates the constraint that guarantees that all flights (rows) are covered at least once. If this equation equals 1 (=1), then it becomes an SP model.

3.3.1. Genetic algorithm optimization

Genetic algorithm have been introduced by Holland [47] to understand the adaptive search processes of natural systems. GAs are inspired by the evolutionary phases of biological organisms in nature. GAs can be applied to combinatorial optimization and machine learning and represent a popular class of EAs [48]. The primary logic of genetic algorithm attempt to improve a population of candidate solutions by iteratively applying a set of genetic operators (crossover and mutation) and creating new individuals then replacing the old individuals with the ones. The proposed GA for solving the crew pairing problem is described in this section.

Representation is the most important part of a GA. Binary coding is used for the crew pairing problem, and two types of models are recommended for the solution to the crew pairing problem by incorporating a GA. These models are column-based presentation [44] and row-based presentation [49]. Column-based presentation is considered in this study.

3.3.1.1. Initialise the population

The initial population is the first stage of the GA. Each chromosome in this population represents a possible solution to a problem. A heuristics approach is suggested to cover each flight while the initial population is generated.

  1. 1

      Procedure InitialPopulation (pairsActive, Flights, Population)

  2. 2

        for (each chromosome in population)

  3. 3

          for (each flight Fi in Flights list)

  4. 4

            if (Fi is covered by pairsActive list)

  5. 5

              if (number of covers in chromosome of Fi < 1)

  6. 6

                find the "crew pairing list" PL that includes Fi out of pairsActive.

  7. 7

                if (PL ≥ 1)

  8. 8

                  select a random pairing P out of PL.

  9. 9

                  insert P to chromosome.

  10. 10

          add chromosome to Population.
Algorithm 3

Initial population algorithm

We generate the initial population using the InitialPopulation method with the pairsActive and Flights lists. The pairsActive list is a pairing subset that is chosen among all pairings and covers each flight at least n time(s). The Flights list is a set in which all flights exist. The populationSize points to the chromosome number in the population. In line 2, the “for” loop activates each chromosome in the population. In lines 3 and 4, whether any pairing in pairsActive covers each Fi flight is verified. If this Fi flight is covered, then whether this flight has been covered before in the genes of the chromosome in line 5 is verified. If this Fi flight has not been previously covered in the genes of the chromosome, then the pairings that cover this flight in line 6, i.e., crew pairing list (PL), are identified. In lines 7, 8 and 9, if there is a pairing P that covers this flight and the number of pairings is more than one, then a P is randomly chosen among the PL and added to the chromosome; in other words, the related chromosome’s gene is true. The loop starts for the first chromosome of the population. After all flights are activated, the loop is added into the chromosome list in line 10 and continues until the break condition is met.

3.3.1.2. Fitness function

The fitness value of a chromosome equals the objective function of the problem. The fitness value indicates the degree to which a chromosome fits the structure of the objective function (max or min). The main objective is to minimize the total cost of the objective function. The fitness function is used to calculate the cost of each chromosome in the population. The best set solution (chromosome) must cover all flights in the airline’s timetable. Calculating the fitness function is not standard, and although similarities may be observed, each work is unique. The fitness function adopted in this study is defined in Eq. (5) using the following terms:

cj=

cost of pairing j;

si=

cost of flight i;

hj=

hotel transportation cost of pairing j;

nj=

number of night stays of pairing j;

i=

1,2 … … … f (f Є F: set of all flight legs);

j=

1,2 … … … p (p Є P: set of all pairings).

Fitness function (Min)=∑j=1p(cjxj+∑i=1fsiyi aij)+∑j=1pnjhjxj

Parameters of the model;

cj > 0, si > 0 and hj > 0;

x(j)∈{0,1} ∀j∈Px(j)    ={10if pairing j is selected; otherwisey(i)     ={10if flight i is a deadhead;otherwisea(i,j)={10if flight leg i is covered by pairing j;      otherwise

Eq. (5) shows that the first statement of the equation provides the total cost of the crew pairings in the solution set of the chromosomes (see details in Section 3.1). The second statement provides the total deadhead cost that would occur in the event of multiple coverages of a flight in the solution set. Deadheads represent the crew staff, excluding the actual commissioned crew, who travel to another base as passengers on the aircraft. If a flight is covered more than once, then the flight would bring an extra cost to the airline. The penalty value here is calculated by setting it equal to the cost of a deadhead flight. The third statement is the hotel transportation costs.

3.3.1.3. Genetic operators

Because the crossover and mutation operator is the stage of transferring genetic information to the new generation, the selection phase of the chromosomes that cross will be important. In this study, a binary tournament selection method was used because it performed better than other selection operators. After selecting the ancestor (mother and father) chromosomes to produce new children, the crossover operator is applied. Single point crossovers, two point crossovers, and uniform crossings have been attempted using crossover operators, and the single point crossover is the best performing operator of the algorithm. The bit-flip mutation operator was applied to ensure that the algorithm does not catch local (local) maxima and local minimum spots.

3.3.1.4. Local search heuristics

3.3.1.4.1. Repair heuristic

The child chromosomes obtained after the crossover and mutation processes are not guaranteed to be feasible. Beasley and Chu [44] attempted to repair non-feasible chromosomes that could be formed by the method they proposed. A chromosome should be covered by each leg in flight set. Eq. (6) determines the crew pairing that should be added to the solution set to cover unscheduled flights.

Cost of crew pairingNumber of non covered flights included in CP

As a first step, to make non-feasible chromosomes feasible, flights not covered in the solution set and the possible crew pairings that can be included in the solution set to allow these flights to be covered in the solution set are identified. The above equation is used to determine which crew pairings to include in the solution set so that non-covered flights are covered. The steps of the algorithm used in the study are as follows (Algorithm 4):

  1. 1

      Procedure Repair (Flights, pairsActive)

  2. 2

        initialize notCoveredFlightList = {}

  3. 3

        for each flight Fi in Flights do

  4. 4

          if (Fi can not be covered by chromosome)

  5. 5

            Insert Fi to notCoveredFlightList;

  6. 6

        if (notCoveredFlightList is empty such that all flights covered in the solution)

  7. 7

          exit;

  8. 8

        for each flight Fj in notCoveredFlightList do

  9. 9

          find the best (according to Eq. 6) pairing Pi out of pairsActive that covers Fj

  10. 10

         add Pi to chromosome.

  11. 11

         update notCoveredFlightList (remove all flights of Pi from notCoveredFlightList).
Algorithm 4

Pseudocode of the repair

The pseudocode for the repair of unsuitable chromosomes is shown in Algorithm 4. For the Repair function in line 1, the Flights and pairsActive lists are used as input. Flights is the list of all flights, and pairsActive (subset) is a pairing subset selected from the pairings in pairsAll that covers all flights. In line 2, notCoveredFlightList is generated for the flights that are not covered in the solution set (chromosome). Between lines 3 and 5, whether all flights in the flight list are covered in the solution set is determined, and the flights that are not covered are added to the notCoveredFlightList set. In lines 6 and 7, if all flights are covered, the solution ends. In line 8, optimum pairing is searched for each flight that is not covered in the notCoveredFlightList set. In lines 9 and 10, the best pairing is found according to equality 4, and the found pairing is added to the solution set (pairsActive). In line 11, if each flight other than Fj in this pairing covers one of the flights in the notCoveredFlightList set, then this flight is removed from the notCoveredFlightList set.

3.3.1.4.2. Modified best-improvement local search method

A local optimization step is incorporated to render the solution algorithm more effective. This algorithm is a local optimization process that ensures that the fitness of a chromosome is not impaired once it is made feasible, even when it is omitted from the solution set of redundant crew pairings [44]. This process is implemented immediately after the initial population and mutation processes. Many strategies can be applied for the LS and include (1) first improvement and (2) best improvement. Here, best improvement of the LS is applied. To obtain the best improvement using this strategy, all possible moves are tested for a solution so that the best neighbouring solution can be selected [48]. The pseudocode for the best improvement is given in Algorithm 5.

  1. 1

      Procedure LocalSearch (Population, Flights, pairsActive)

  2. 2

        for (each chromosome in population)

  3. 3

          for (each pair Pi in pairsActive)

  4. 4

            if (Pi is covered by chromosome)

  5. 5

              setGene (Pi, false)

  6. 6

              if (all flights in Flights not covered by chromosome)

  7. 7

                setGene (Pi, true)
Algorithm 5

Local optimization heuristic

Even if crew pairings are removed from the solution set, the pseudocode of the local optimization heuristics where the chromosome compliance is not violated is as presented in Algorithm 5. In line 2, the algorithm runs for each chromosome in the population. In line 3, the loop runs for each pairing Pi for pairsActive. In lines 4 and 5, if Pi is in the solution set, then it is removed from the Pi solution set. In lines 6 and 7, if all flights in the Flights set are not covered, then Pi is returned to the solution set.

3.3.1.5. Population replacement strategies

The last step of the GA is population replacement. In this step, the surviving parent and child chromosomes are selected. Because the number of populations is fixed, a chromosome selection strategy ensures that this number remains fixed. The two main approaches used in the population replacement stage are the generational and steady-state approaches [48]. This study adopts the steady-state approach. An elitist approach is also tested; however, the steady-state approach is preferred because it delivered better results. In this approach, one or two offspring are generated in each iteration. Then, this child chromosome replaces (1) the worst individual in the population or (2) its parents.

3.4. Update heuristics

3.4.1. Deadhead-minimizing pairing search heuristic

This stage can be considered an alternative pairing search stage. The purpose of the developed heuristics approach is to decrease the number of deadheads because they decrease passenger capacity and crew utility efficiency. Therefore, the airlines always require that the number of deadheads be kept at an optimum level [13]. The best chromosome among those in the population is identified first, and the remaining chromosomes in the population are then removed from the solution set. In addition, the best chromosome is an alternative solution. Finally, alternative pairings that will decrease the number of deadheads are searched by checking how many times each flight was covered among the best chromosome, i.e., pairings in the alternative solution. This search procedure is conducted between all pairings that are generated, starting from the ones that cover deadheads the most, and alternative identified pairings are added to the subset. An example alternative pairing search that will decrease the number of deadheads is shown in Fig. 3.

Fig. 3.

Alternative pairing search example.

In the above example, the most covered flight among the pairings in the best chromosome is f3. The pairings that cover this flight are shown as Px1, Px2 and Px3, and the flight legs are f1, f2, f3, f4, f5, f6 and f7. The alternative pairings that cover f3 together with f1, f2, f4, f5, f6 and f7 among all pairings are Py1, Py2, Py3 and Py4. Although flight f3 in the best chromosome is covered by pairings Px1, Px2 and Px3, it can be covered by pairings Py2 and Py3 together with all flights by the suggested method. Here, the aim is to make more than one flight covered in the solution set minimum. In this manner, the costs in the goal function can be decreased.

  1. 1

      Procedure SearchForDeadheadMinimizingPairs (bestChromosome, Flights, pairsAll, pairsActive)

  2. 2

        initialize pairsActive = bestChromosome.pairs

  3. 3

        While (true)

  4. 4

          find the next flight Fi that is covered by the solution the most

  5. 5

          if (Fi can not be found)

  6. 6

            exit;

  7. 7

          find the "crew pairing list" PL that includes Fi out of pairsActive.

  8. 8

          find the "flight list" FL that includes all the flights that are covered by PL.

  9. 9

          search for a “new pairing list” NPL out of pairsAll that covers all flights in FL with no deadheads.

  10. 10

          add all pairings from NPL to pairsActive.
Algorithm 6

Pseudocode of the deadhead-minimizing pairing search

An alternative pairing search algorithm pseudocode that will decrease the number of deadheads is shown in Algorithm 6. In line 1, the bestChromosome, Flights, pairsAll and pairsActive lists are used as input for the SearchForDeadheadMin function. bestChromosome includes the genes of the best chromosome (of the solution set) obtained as a result of a certain iteration study of the GA, i.e., the list of pairings; Flights is the list of all flights; pairsAll is the list of all pairings; and pairsActive (subset) is a pairing subset that is chosen among the pairings in pairsAll that covers all flights. In line 4, the flights Fi that are most covered in the solution set (bestChromosome) are present. In line 5 and 6, if no Fi is found to be covered more than once, then the solution ends. In line 7, pairings that cover flight Fi are found in pairsActive, and the PL list is generated. In line 8, the flight list, i.e., the set FL, which is covered by PL and includes all flights, is found. In lines 9 and 10, new pairings that cover all flights in the FL list and do not include any deadheads are searched, and the NPL list is generated. Then, all pairings in the NPL list are added to the pairsActive list.

3.4.2. Less-costly alternative pairing search

The less-costly approach can be called the partial solution search. This approach is a procedure for searching for high-quality pairings (low-cost) from the main set (pairsAll) to replace low-quality pairings (high-cost) from the best chromosome or subset (pairsActive). In other words, the approach can be called the low-cost pairing search procedure. Initially, the pairing with the lowest quality is identified, and a high-quality pairing search is conducted in the main set for flights in the pairing with the lowest quality. This continues until high-quality pairings are found for flights in the pairing with the lowest quality. First, a quality index (QI) is identified, and it is calculated as shown in Eq. (7). According to the values of this index, the pairings are listed from highest quality to lowest. The pairing with the smallest index value corresponds to the pairing with the lowest quality.

Quality Index (QI)=Total block timeTotal pairing time=∑i=1faij Mifly∑j=1d∑q=1d(bjk Mjtft+bjkbqkhjqMjqrequiredRest)∀ k=1,2,….,p

Notation Define
Mifly The flight time of flight i.
Mjtft The total duty time of duty j.
aij If flight i is covered by duty j, aij = 1; otherwise, aij = 0.
bjk If duty j is covered by pairing k, bjk = 1; otherwise, bjk = 0.
bqk If duty q is covered by pairing k, bqk = 1; otherwise, bqk = 0.
hjq If duty j follows duty q, hjq = 1; otherwise, hjq = 0.
MjqrequiredRest The required rest time between two consecutive duties j and q.
Table 5.

Mathematical notation of the quality index.

i

=1,2,….f (f Є F: set of all flight legs)

j

=1,2,…,d (d Є D: set of all legal duties)

k

=1,2,…,p (p Є P: set of all legal pairings)

The pseudocode of the alternative pairing search algorithm that will decrease the number of pairings with low quality is shown in Algorithm 7. According to this algorithm, an example of a less-costly pairing search with four pairings and thirteen flights is depicted in Fig. 4. In line 3, the pairing with the lowest quality, Pi, is found in the best chromosome. Here, the algorithm starts searching from the pairing with the lowest quality. Then, after the pairing with the lowest quality, we aim to find the next pairing with the lowest quality. In lines 4 and 5, if Pi cannot be found, then the solution ends. In line 6, this pairing is used as an initialized value for the flights in Pi in the searchFlights set. In line 7, the coveredFlightList set is generated for the searched flights. In line 8, a low-cost/high-quality pairing is searched for each flight Fi in the searchFlights set. While conducting the search, this flight should not be covered by the coveredFlightList set at the same time. In line 9, the best pairing Pn (new pairing) that covers flight Fi in pairsAll is found, and this pairing is added to pairsActive in line 10. In line 11, all flights of the chosen Pn are added to the coveredFlightList list. In line 12, a search is conducted of Pn for each flight Fj. In line 13, a low-cost Pj that covers flight Fj is found. In line 14, all flights that are not covered in the new pairing Pj (and those that are not covered in the coveredFlightList set) are added to the searchFlights set.

Fig. 4.

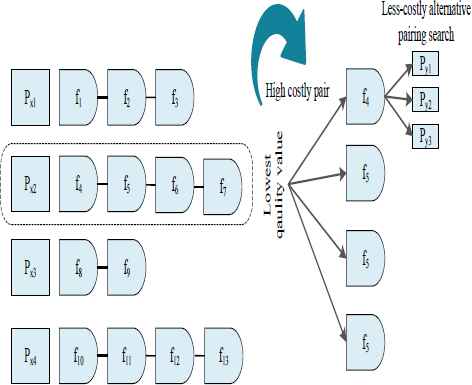
Alternative less-costly pairing search example.

  1. 1

      Procedure SearchForLessCostlyAlternativePairings (bestChromosome, pairsAll, pairsActive)

  2. 2

        While (true)

  3. 3

           find the next pairing Pi that has the lowest quality value (a metric that is used to give quality points to pairings, with higher points indicating better quality) out of bestChromosome.pairs.

  4. 4

          if (Pi can not be found)

  5. 5

            exit;

  6. 6

          initialize searchFlights = flights of Pi

  7. 7

          initialize coveredFlightList = {}

  8. 8

          for (each flight Fi that is in searchFlights but not in coveredFlightList)

  9. 9

             find the best (according to the quality metric) pairing Pn out of pairsAll that covers Fi but does not include any of the flights in coveredFlightList.

  10. 10

            add Pn to pairsActive.

  11. 11

            add all flights of Pn to coveredFlightList.

  12. 12

            for (each flight Fj that is in Pn)

  13. 13

              find the pairing Pj that covers Fj in the last solution (bestChromosome.pairs).

  14. 14

              add all uncovered flights (those not in coveredFlightList) of Pj to searchFlights.
Algorithm 7

Pseudocode of the less-costly alternative pairing search

3.5. General overview

The final status of the solution approach of the crew pairing optimization problem is indicated in Fig. 5 and Algorithm 8. As shown in the algorithm, flight legs are taken from the airline’s timetable as input. In line 3, all possible duties are generated from the flight legs that are taken as input. In line 4, all possible pairings are generated by taking duties that are generated in line 3. In line 5, pairsActiveList is a function that generates a pairing subset that is chosen from pairsAll. In line 6, we generate the initial population using the Flights and pairsActive lists. In line 7, the loop runs until the break condition is met. In lines 8, 9, 10 and 11, optimization is performed with the GA until the loop reaches a certain number of iterations. In line 12, the best chromosome of the population is found at the end of the loop. In line 13, alternative pairings that will decrease the number of deadheads are searched by considering the mostly covered flights of pairings in the best chromosome. In line 14, starting from the pairing with the lowest quality in the best chromosome, alternative high-quality pairings are searched.

Fig. 5.

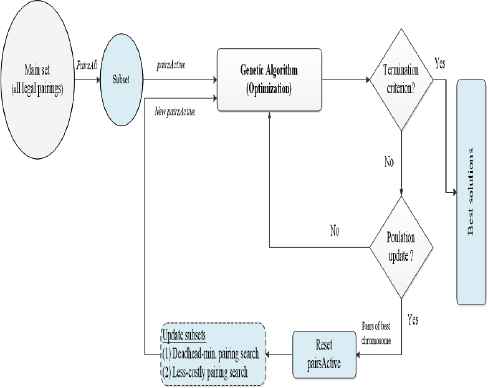
Overview of the proposed approach.

  1. 1

      Procedure Optimization_Crew_Pairing_Problem

       (Flights, maxIteration)

  2. 2

        initialize iteration=0

  3. 3

        dutyList=Generate_Duties (Flights)

  4. 4

        pairsAllList=Generate_AllPairs (dutyList)

  5. 5

         pairsActiveList = initializeActivePairs(Flights, pairsAllList);

  6. 6

       Initialize population (flights, pairsActive);

  7. 7

        While (iteration < maxIteration) do

  8. 8

          Solve_Subset_Genetic_Algorithm (pairsActiveList, Flights)

  9. 9

          If (termination criterion is satisfied)

  10. 10

            Exit;

  11. 11

          If (Update heuristic run is necessary)

  12. 12

            Find the bestChromosome

  13. 13

            Run_Search_Pair_Deadhead_Minimizing_Approach (bestChromosome, Flights, pairsAllList, pairsActive)

  14. 14

    Run_Search_Less_Costly_Alternative_Pair_Approach (bestChromosome, Flights, pairsAllList, pairsActive)

  15. 15

          iteration++

  16. 16

        end While
Algorithm 8

Overview of the proposed algorithm

4. Computational Results

The flight data used in this study are associated with the airline timetable of the A310 fleet owned by an airline company in Turkey. This schedule includes 591, 608, 714, 810, 906 and 1002 monthly flight legs for testing. The programme was run on a computer with an Intel® Core ™ 64 2.40-GHz processor on the Java Eclipse platform. Each trial was repeated 30 times. This study assumes that all crew members reside in Istanbul (IST). The test instances and flight legs are presented in Table 6.

Instances Flights legs Duties Pairings (main set)
1 591 1826 82332
2 608 1907 88624
3 714 2064 208255
4 810 2467 320866
5 906 2771 532115
6 1002 3333 1121408
Table 6.

Legs and pairings of test instances.

The GA is executed for 20,000 iterations, and a subset is updated once every 1000 iterations (excluding pairings of the best chromosome). In this manner, the length of the chromosome dynamically changes once every 1000 iterations. Parent selection is performed using binary tournament selection with a tour size of 4. The population size is set to 30, and the crossover probability is set to 0.8. For each generation of an EA, only two offspring are generated, and they replace the worst individuals of the parent population.

The duties column in the table above shows the total number of duties generated from monthly flight legs. These duties are generated with a depth-first search algorithm. The pairing column indicates the total number of pairings (the main set) that are generated within the framework of legal restrictions using the duty list. In the same manner as for the duty enumeration, a depth-first search algorithm is used to generate all legal pairings.

In this study, this problem is integrated into three different EAs as an optimization problem: (1) two GA variants and (2) a MA. The overall structure of the proposed EAs (GA1, GA2 and MA) is shown in Table 7.

Improving Heuristics Evolutionary algorithms
GA1 GA2 MA
Deadhead-minimizing pairing searching x x x
Less-costly alternative pairing searching - x x
Local optimization techniques - - x
Table 7.

Proposed evolutionary algorithms.

In GA1, a subset is formed by a deadheadminimizing pairing search. The initial population of individuals is created randomly. A repair heuristic is then applied on each and every individual within the initial population. Subsequently, in each iteration cycle, two parents (individuals) are selected using the binary tournament selection method. This method chooses the individual with the best fitness among several randomly chosen individuals from the initial population with the tour size. Two new children are then created by applying the crossover to those selected parents, and the children are mutated afterwards. A repair heuristic is applied to potentially non-feasible chromosomes. Then, the worst two individuals in the population are replaced with the best two of the parents and offspring. The subset is updated in each specific iteration until the termination criterion is satisfied. Finally, the best solution is identified.

In the second approach, GA2 is used. Similar to GA1, GA2 starts with a randomly generated initial population and applies repair heuristics to each individual in the population. Deadhead-minimizing and less-costly pairing search algorithms are integrated and used in GA2. Third, after forming the initial population of GA2, a local optimization technique is applied, and this algorithm is called an MA. The other steps in the MA are the same as those of the GA (GA2).

MAs and GAs developed by other authors have also been tested, and the results are provided in Table 8. The KPIs in this table show that among the proposed algorithms, the MA generated better results. However, statistical methods should be used to determine whether significant differences occurred between these algorithms.

Table 8.

KPI-Cost report I for proposed approaches.

The Mann-Whitney-Wilcoxon test is used as a statistical test of the pairwise average performance of two given algorithms for non-parametric tests [50]. The results show that the proposed MA provides less-costly crew pairings.

The proposed algorithm was compared with the results of previous studies performed with the same EAs, and the results show that it exhibits significant performance. Kornilakis and Stamatopoulos [14] and Zeren and Ozkol [13] sought to eliminate poor-quality crew rotations to reduce performance problems in their studies, and they successfully eliminated poor-quality crew pairings as long as they stored high-quality crew pairings of a certain amount.

In other words, a pairing subset is generated by choosing a pairing of a certain amount from the main set of all pairings, and it is provided to the GA as input. The difference in our study is that the pairing subset is dynamically and continuously renewed because the GA is optimized. Comparisons of previously proposed MA approaches are summarized in Table 9.

Table 9.

KPI-Cost report II for performance comparisons of previously proposed memetic algorithm (MA) approaches.

Three important parameters are presented in Tables 8 and 9: total man-days, deadheads, and layovers/overnights. The solutions are generally evaluated via these three parameters. Evaluating other parameters is meaningful if these three values are close to each other. Because financial costs are not determined, the total cost can provide insights for planning, although the solutions are always evaluated with the three important parameters because of operational difficulties. According to the planning period, the overnight, deadhead and man-day parameters are prioritized based on their level of importance.

Novel dynamic-based GA variations and a MA approach are proposed to obtain a crew pairing solution set with the minimum cost. In Fig. 6, graphics are shown for the following KPIs (e.g., instance 6) obtained via the optimization of the proposed approaches: number of deadheads: total number of deadheads; deadhead time: total flight times of deadheads; duty days: total number of duty days; overnight stays: total number of overnight stays; overnight duration: total time of overnight stays; and fitness: total crew pairing cost.

Fig. 6.

Summary of the KPI to compare the proposed approaches (instance 6).

In Table 10, a summary of the critical assessment parameters of the crew pairing is shown, and it indicates that the proposed approach is successful at decreasing the total deadhead time. The deadhead factor is an important KPI, especially in high seasons because the airline’s income will decrease when passenger seats are used by the crew. Another important KPI is the number of duty days. In certain months, the airline companies encounter difficulties securing a sufficient number of pilots, particularly in December when certain pilots have reached their annual flight time limits. Therefore, the number of duty days is an important factor. The number of overnights is another factor that must be at the optimum level because it affects the accommodation costs of the airline companies. The total cost value shows a general optimization performance. The results show that the proposed approach generates outstanding total cost values.

Note: KS=Kornilakis and Stamatopoulos [14] and ZO=Zeren and Ozkol [13].

Table 10.

Summary report with percent improvement (%).

Fig. 6 and Table 10 show that the MA-generated solutions present better deadhead, duty day, overnight stay, and total cost values.

5. Conclusions and Future Directions

In this study, a dynamic-based MA approach and GA variations are proposed for the airline crew pairing problem, which has been intensively studied in the literature. Because crew pairing is a main cost-identifying stage of the crew scheduling process, approaches that decrease crew costs, increase crew utility and generate optimum crew pairings are of significant importance. KPIs, such as deadhead time, number of duty days, and number of overnight stays, are submitted along with the financial costs related to crew pairing optimization. These indicators are of significant importance because they facilitate the management of operational challenges in real-world problems.

A unique model and strategies have been developed after reviewing current approaches during the development of the proposed solution. The computational results section shows that the proposed strategy generates highly competitive results when compared with current approaches. The proposed approach is particularly successful at decreasing deadhead time and the number of overnight stays.

The main contributions of this study are as follows:

  • •

    A dynamic-based GA has been developed for solving the medium-scale airline crew pairing problem;

  • •

    An alternative pairing search (deadheadminimizing search) approach has been developed that will decrease the deadhead factor;

  • •

    A low-cost (high-quality) alternative pairing search (partial solution search) approach has been developed.

Dynamic-based GAs and changes in chromosome length in each iteration were used to resolve the crew pairing problem. The advantage of the proposed approach is that it seeks the solution set with the minimum cost that covers all flights via a GA by generating subsets from millions of main sets. However, using millions of generated crew pairings in the GA as direct input renders the problem impossible to solve and slows the performance of the algorithm, thereby leading to sub-optimal results. Therefore, one subset is considered instead of all pairings. This subset dynamically changes, i.e., the main set and the subset exchange pairings. The pairings that lead to a suboptimal solution from the pairing subset are excluded from the solution, and the pairings that lead to an optimal solution from the main set are chosen and added to the subset.

The second contribution is an alternative pairing search approach that will decrease the number of deadheads. In this method, a heuristics approach that searches and finds the pairings that generate the fewest deadheads for each flight is developed, and it sends the pairings that lead to the best solution from the main set to the subset. Concurrently, the approach checks the number of covering flights in the pairings in the subset as explained in Section 3.4.1. If a flight is covered more than once (deadhead) in the pairings, the alternative pairings that decrease the number of deadheads are sought. This search is performed for all pairings starting from the deadhead that is most covered, and it adds the identified alternative pairings to the subset.

The third contribution is that high-quality pairings are searched from the main set and low-quality pairings in the subset are not searched by checking the pairings in the best chromosome. In other words, a low-cost pairing search is performed. As stated in Section 3.4.2, the pairing with the lowest quality is first identified, and then a high-quality pairing search is performed from the main set for the flights in the pairing with the lowest quality for this lowest quality pairing. This procedure continues until it finds the highest-quality pairings for flights in the pairings with the lowest quality. This procedure is conducted according to the quality metric that is assigned to the pairings beforehand.

Detailed comparisons are presented in the tables above, and they clearly show that the proposed approach can generate competitive results when compared with current approaches that use state-of-theart solvers (the deadhead-minimizing pairing search and less-costly alternative pairing search algorithms).

Acknowledgements

This study has been supported by the Yildiz Technical University Scientific Research Projects Coordination Department, project number 2014-06-03-DOP01. The authors would like to thank the Turkish Airlines Crew Planning Department for their help and feedback in this research project.

References

1.C Barnhart and KT Talluri, C ReVelle and A McGarity (editors), Airline operations research in design and operation of civil and environmental engineering systems, Willey, 1997, pp. 435-469.
2.M Bazargan, Airline operations and scheduling, 1st Edition, Ashgate Publishing, Ltd.., USA, 2004.
3.M Bazargan, Airline operations and scheduling, 2nd Edition, Ashgate Publishing, Ltd.., USA, 2010.
5.A Ekenback, A column generation heuristic for a combinatorial optimization problem, MsC’s in Computer Science at the School of Engineering Physics, Royal Institute of Technology, 2002.
12.M Deveci and ND Cetin, Airline Crew Pairing Problem: A Literature Review, in 11th Int. Sci. Conf. on Eco. and Soc. Dev. – Building Resil. Soc. (Zagreb, Crotia, 2015), pp. 103-110.
38.P Moscato, On evolution, search, optimization, genetic algorithms and martial arts: Towards memetic algorithms, Caltech concurrent computation program, Vol. 826, 1989, pp. 1989. C3P Report
39.C Altıntas et al., Self-generating memetic algorithm for examination timetabling, in 10th International Conference of the Practice and Theory of Automated Timetabling (York, UK, 2014).
41.MR Garey and DS Johnson, Computers and Intractibility: A Guide to the Theory of NP-Completeness, Books in the Mathematical Sciences, Vol. 44, No. 2, 1979.
45.S Kerati et al., A heuristic Genetic Algorithm approach for the airline crew scheduling problem, EU/ME, the European chapter on metaheuristics, EURO Working Group, 2002.
46.Republic of Turkey Ministry of Transport, Maritime Affairs and Communication, Instruction on Flying Team’s Task and Resting Terms and Principles of Application, 2014.
47.J Holland, Adaptation in natural and artificial systems, University of Michigan Press, Ann Arbor, MI, 1975.
49.LFG Hernandez and DW Corne, Evolutionary Divide and Conquer for the Set-Covering Problem, AISB Workshop on Evolutionary Computing, Springer, Berlin Heidelberg, 1996.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
10 - 1
Pages
1082 - 1101
Publication Date
2017/07/20
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.2991/ijcis.2017.10.1.72How to use a DOI?
Copyright
© 2017, the Authors. Published by Atlantis Press.
Open Access
This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Nihan Çetin Demirel
AU  - Muhammet Deveci
PY  - 2017
DA  - 2017/07/20
TI  - Novel search space updating heuristics-based genetic algorithm for optimizing medium-scale airline crew pairing problems
JO  - International Journal of Computational Intelligence Systems
SP  - 1082
EP  - 1101
VL  - 10
IS  - 1
SN  - 1875-6883
UR  - https://doi.org/10.2991/ijcis.2017.10.1.72
DO  - 10.2991/ijcis.2017.10.1.72
ID  - Demirel2017
ER  -