A Fuzzy System for Estimating Premium Cost of Option Exchange Using Mamdani Inference: Derivatives Market of Mexico
- DOI
- 10.2991/ijcis.2017.10.1.11How to use a DOI?
- Keywords
- Fuzzy logic; defuzzification; financial risk; Mamdani fuzzy inference system
- Abstract
The calculation of the premium cost of an option exchange is usually computed by the different mathematical models that obtain the degree of uncertainty in the financial market by Black-Scholes method though such a degree is inaccurate. In order to improve the management of uncertainty the use of fuzzy logic makes possible to capture a better reality of the derivatives market in an uncertain environment. Therefore, this paper aims at introducing a Fuzzy Inference System to estimate the Premium Cost of an option exchange (FISPC) by using the Mamdani based inference system to provide managers a supporting tool for the implementation of design of strategies for the management of financial risk with the purpose of minimizing exchange risk. For a better understanding of the proposal and to validate the good performance of FISPC, it will be developed and applied in the Derivative Market in Mexico and its results compared with Black-Sholes theoretical model. Eventually, an analysis of the results and the impact of managing financial risks with FISPC in the event of volatility in the financial markets are provided.
- Copyright
- © 2017, the Authors. Published by Atlantis Press.
- Open Access
- This is an open access article under the CC BY-NC license (http://creativecommons.org/licences/by-nc/4.0/).
1. Introduction
Determining the cost of the premium for an exchange option is an important issue in financial risk management area. It allows establishing financial strategies by using derivative instruments in financial markets to cover efficiently and minimize financial risks. Financial markets are characterized by increased volatility. The economic indicators that directly influencing volatility are interest rates, exchange rates, inflation, government economic policy or fiscal policy, among others [1]. Global derivatives market represents 730 trillion dollars a year, reflecting its importance for the impact on world economies [2]. The first studies on risk management, were made under a certain economic and financial stability, when there was a fixed exchange rate regime change in Bretton Woods System in 1972. Since its disappearance an exponential increase occurs in the volatility of financial markets. The authors whose contributions were fundamental to the study of risk: Markowitz developed portfolio theory and proposed the concept of covariance and correlation [3]. Sharpe developed the model Capital Asset Pricing Model [4]. Black and Scholes proposes model for the valuation of options [5]. Scott and Tucker propose the analysis of volatility through time series model, but with certain methodological limitations that do not permit formal hypothesis testing [6]. Merton said that application of derivative reduces systemic risk [7]. JP Morgan proposed the VaR to quantify exposure to market risk, but considered only loss as a risk and no other variables [8]. Hull & White, Chang, Jorion propose stochastic models to better estimate and assessment of the behavior of economic variables [9]. Looking at Mexico, the main causes of volatility are the constant devaluations undertaken by government, which has had a high financial impact on organizations.
In this context, stochastic models are still insufficient to formalize human processes, especially because of its rigidity. Therefore, they can be inaccurate for determining the cost of the premium of exchange option, in volatile and uncertain environments, when they do not consider the human factor in decision-making [10]; generating a greater exposure to exchange risk. There are different models for determining the cost of the premium; including Black and Scholes model, logarithmic binomial tree, Monte-Carlo simulation model, among others [11]. These economic and financial models based on static theories, which are based on reasoning from the simplification of the reality, can deal with stochastic volatility. However, stochastic models based on classical logic are limited to stable conditions in financial markets. The generic applications of Black-Scholes model are limited by its nature and it is not suitable for the average fuzzy environment from decision-making [10]. However, they applied this model with the inclusion of fuzzy logic for determining the price of an option from interest rates, to better capture the reality in the derivatives market to a fuzzy environment. Empirical evidence of statistical bias is due to the fact that, the volatility of financial markets in the major variables that makes up the Black-Scholes model [12].
Therefore, to overcome previous limitations, the application of fuzzy logic [13] facilitates to capture a better reality of the derivatives market under uncertainty. Hence, this paper aims at introducing a Mamdani fuzzy inference system model [14] for estimating premium cost of option exchange with linguistic rules established by the experts. Considering exogenous variables of the economy that affect the volatility of the financial markets; that traditional models do not capture in short periods. Its application will allow a greater optimization of the decisions since it generates possible price variation scenarios that are possible at the time of exercising the option. FISPC will be developed and applied in the Mexican derivatives market (MexDer); considering that its input variables will be based on the application of econometric models in the exchange rates forecast, foreign and domestic interest rates, and expert opinions. The results obtained by FISPC on the MexDer will be compared with the Black-Scholes method to show its better performance and higher adaptability to volatile markets.
This paper is organized as follows: Section 2 provides a literature review about risk management, fuzzy logic, and Mamdani fuzzy systems. In Section 3 is developed the FISPC within the data of MexDer to estimate the premium cost of an option exchange. Section 4 develops a performance comparison between FISPC and Black Scholes model providing an analysis of the results obtained. Conclusions are drawn in Section 5.
2. Preliminaries
This section reviews in short some necessary concepts for understanding our proposal to determine of the premium cost of an exchange rate option regarding financial risk management, fuzzy logic, fuzzy systems and Mamdani fuzzy inference system
2.1 Financial risk management
Financial risk is a main task in senior management; some organizations take it passively; others see it as a competitive opportunity. These are related to the dynamics of change and possible losses in financial markets; the movements in economic variables such as interest rates and exchange rates are an important source of risk for most organizations. Its administration allows decision making for reducing the adverse impact that these fluctuations can have on working capital and profitability [12]. As such, risk management occurs due to the exponential growth of derivative instruments and the volatility in the financial markets. During the past decades its development has gained greater strength due to the need of the organizations to have control over uncertainty of a market that is in constant change. Financial risk management as the process of decision-making and ensuring that these decisions are put to work, in relation to the management and control of the impact that in the organization has the variation in the expected results of those events that have a possible result of gain/loss, to which it is exposed [15]. This process generally managed by the financial departments, treasuries, trading and the market is usually related to positioning strategies or hedging via financial instruments, derivatives as forward, swaps, futures, options, etc.
Thus, with the advance of the financial industry beginning with the economic globalization, a structural change has occurred in the International Financial System. Such a change has caused the existence of more and more sophisticated models for risk management. The contributions of authors such as Markowitz, Modigliani and Miller, Sharpe, Lintner, Samuelson, Merton, Black and Scholes, J.P Morgan, Hull and White, Chang, Jorion, among others, have revolutionized the economic and financial world [9]. Among them it highlights the Black-Scholes model for the valuation of options which was developed in an ideal condition in the market for the underlying value and choice. Its limitations involve aspects such conditions or assumptions under which it is applicable. Later, Scholes and Merton, improve it by proposing that in determining the value of an option is not essential market equilibrium; all that is required is that no arbitration cases [7]. The main contribution lies in the theoretical and practical significance of the analysis method that has been used in many other economic problems. Hull-White, Johnson & Shannon propose using of Monte Carlo simulation model to estimate the price of the option; but has limitations to its application, as it requires more time and complexity [16]. JP Morgan proposes the VaR to quantify exposure to market risk through traditional statistical measure that has limitations, when the market is in crisis or turbulence, given that considered only loss as a risk and no other variables, so that the values obtained in times of crisis may not be significant [8].
Previous models, based on binary math do not consider the human factor in determining the cost of the premium of the financial instruments of the derivatives market. On the contrary, the non-numerical mathematic allows to use models that capture the human factor in the study of phenomena that escape not only the measurement, but also the valuation; allowing thereby better management financial risk. However, sophistication in the use of techniques and tools has not been a success factor in decision making in an environment of increased uncertainty. Then, traditional methods of binary math do not have the expected efficiency in a volatile and globalized environment; with it opens a space to address subjectivity, vagueness and uncertainty from another perspective [11]. Hence, that increased volatility emanating connectivity markets and economies of unequal size requires rethinking the use of traditional tools and the adoption of new instruments to address the treatment of uncertain phenomena. One of them, supplementing the traditional analysis is the theory of fuzzy sets, which it passes from point responses of binary mathematics to multivalent of fuzzy math [17]. The complexity and dynamics of real-world engineering, financial and economic problems require advanced and sophisticated methods and tools to build hybrid risk assessment tools which can deal more powerfully with issues like fast-learning, uncertainty, online adaptability, knowledge capability and hierarchical solution etc. [18].
2.2 Fuzzy logic
The financial problems of the real world can be too complex to be considered in a formal model; this becomes more evident in the field of organizational economy, where most entrepreneurs make their decisions based on schemes “no quantitative” or “subjective”; they considering their knowledge on the phenomenon. Fuzzy set theory provides a mathematical framework in which vague conceptual phenomena can be precisely and rigorously studied [19]. In this sense, research carried out in this area suggests models to capture these schemes and systems expert reasoning, which can be applied successfully in decision-making.
The fuzzy logic used relative concepts to the reality, to define variables and degrees of membership; following patterns similar to those of human thought reasoning. Fuzzy logic systems can approach the problem of decision making in a strict sense and at the same time support the treatment of uncertainty and vagueness. In addition, the fuzzy logic introduces the possibility of resolving expressed problems from the human perspective and that this simple condition, cannot have a single solution from the “false” or “true,” but may take intermediate conditions to provide solutions satisfactory to the problems presented. For these reasons, fuzzy logic can be found in the field of research on issues related to the social sciences and management, economics, sociology, psychology, among others. Thus, it might then compete with other theories, but it might also be the most appropriate way to model this phenomenon; due to that fuzzy set theory is more adaptable to different contexts [19].
Thus, fuzzy logic can be explained as a system that models non-linear functions, it provides a methodology to model vagueness, ambiguity and the human way of thinking, reasoning and perception. Fuzzy set is a class of objects with a continuous degree of membership [13]. This set is characterized by a membership function, which assigns each object a value between 0 and 1. Besides, a fuzzy set is prescribed by vague or ambiguous properties; hence, its boundaries are ambiguously specified. On the contrary, a classical set is defined by crisp boundaries; its characterized by its membership function may take only two values 0 and fA(x) = 1 ó 0. Memberships for classical and fuzzy subsets are shown in Fig. 1.

Example of (1) classical set and (2) fuzzy set.
2.3 Fuzzy systems
Fuzzy set theory provides foundations for modeling the vagueness and ambiguity in complex systems. Fuzzy sets can be associated as semantics to linguistic labels, whose membership function may assume different values of the interval [0, 1]. The values of the variables linguistic are labels linguistic in function of defined terms in the fuzzy sets, such as for example the linguistic values of the variable height are: very low, low, medium, high, very high [20], illustrated in Fig. 2. The concept of linguistic variable provides a means of approximate characterization of phenomena which are too complex or that are not well defined to be susceptible to quantitative description in conventional terms. Moreover, the linguistic variables are values represented by linguistic terms. The meaning of these linguistic terms is determined by fuzzy sets, which provide a gradual transition of states, have the ability to express and work with comments and measures of uncertainty, in both, by capture measures of uncertainty are more adjusted to the reality that the variables crisp. Also, a linguistic variable is the variable whose values are terms, words or sentences of natural language.

Fuzzy linguistic variables.
The use of linguistic variables provides a basis for approximate reasoning in fuzzy logic that offers a more realistic framework for human reasoning than classical logic. Fuzzy inference systems (Fig. 3) were developed to control complex processes by means of the human experience, from a set of linguistic rules, in which words are modeled by fuzzy sets [19].

Diagram of a fuzzy inference system, based in Zimmermann [19].
Fuzzy systems consider a subjective assessment which is characterized by terms of fuzzy (IF-THEN) rules. A fuzzy rule is the basic unit for capturing knowledge in fuzzy systems. A fuzzy rule has two components: an “if” clause, an antecedent, it is a condition of application domain; and a “then” clause, a consequence it is an action of control given to the process under control. The final output is a fuzzy set created by the superposition of individual rule actions.
2.4 Mamdani fuzzy inference systems
The main idea of the Mamdani method is to describe process states by means of linguistic variables and to use these variables as inputs to control rules [21]. A Mamdani-type fuzzy model involves developing membership functions and defining the subsequent rules. The rules connect the input variables with the output variables and are based on the fuzzy state description that is obtained by the definition of the linguistic variables [19].
The basic components of a Mamdani Fuzzy System are: fuzzification, knowledge base with its inference system and defuzzification. Meanwhile, general structure of fuzzy model included the input variables, the development of rules and output variable.
- i.
Fuzzification, understood as the introduction of input values and their interpretation as linguistic values, determined membership functions of the system variables in the fuzzy sets. The universe of discourse of each variable was determined by the linguistic components “Very low”, “Low”, “Medium”, “High” and “Very high” for input and output.
- ii.
The knowledge base consists of fuzzy rules (see Fig. 4) defined with the help of experts. Each row of membership functions constitutes an IF–THEN rule with the logical intersection operator “AND”. The inference function takes the membership degrees of the fuzzification supported in the rule base to generate the output of the fuzzy system. Depending on the values used, the input membership functions are activated to a certain degree. The contributed output from each rule reflects this degree of activation and obtains a fuzzy output by superposition of individual outputs.
- iii.
Defuzzification is used to obtain an output from the previous fuzzy set. It is usually used centroid method. Subsequent defuzzification produces a crisp value output.
Rule structure in a fuzzy system.
3. A fuzzy inference system to estimate the premium cost for the Mexican derivatives exchange option
In global economy, financial markets are characterized by a growing volatility. Black-Sholes model (B-S) is more rational model to prevent average uncertainty during the life of an option exchange since it is the one with greatest approval by financiers due to its practical application to determine option pricing in the derivatives market. This model used for fixing the value of exchange rate options [9]. B-S model is a universal standard within the valuation of European options [22]. However, the use of fuzzy logic to the estimation of financial risks allows broadening the field for the development of more flexible and adaptable economic models “to model the behavior of economic agents and incorporate to the analysis the ambiguity in human beings” [23].
This section introduces a fuzzy inference system to estimate the premium cost (FISPC). Such a fuzzy system is developed on the MexDer, i.e., the Mexican derivatives exchange option market. Such a fuzzy system follows the general architecture of a Mamdani fuzzy inference system revised in Section 2.4. The overall approach followed in this study is illustrated in Fig. 5. The process begins with knowledge acquisition, continues to model building and then finally testing the model performance. The development of the Mamdani inference system will be supported by Fuzzy Inference System Toolbox of Matlab 7.1.

Overall approach to develop the FISPC.
The different components of the FISPC will be further described below.
Among the economic indicators that influence financial markets: interest rates, exchange rate, inflation, the government economic and fiscal policy, are important among others. Due to the fact that FISPC aims at estimating the premium cost of a Mexican exchange option by using data from the Mexican Derivatives Exchange. It is necessary a further detailed description of the variables used by FISPC in the fuzzification and defuzzification processes.
The input and output variables are established considering the economic theory and economic factors that determine the cost of a purchase option. In this sense, the selection of variables implies emphasizing the ones that allow indicating an economic outlook in which a result that directly influences the prime cost is expected. The economic theories consider the existing connections between real variables that determine the international trade, the exchange rates fixed in the financial markets and levels of investment.
Therefore, exchange rate is the most used mechanism by the Bank of Mexico in the monetary policy; for this reason, it will be the first input variable in FISPC. It was also considered that in the economic models to determine exchange rate, the exchange variation is the most decisive factor in an option´s price. Hence, the second input variable defined in FISPC was the CETES (Treasury Certificates) interest rate since the monetary policy-making in Mexico is conditioned by the volatility of the return of government bonds that are internationally valued and measure the impact that they have in the interest rate. And the third input variable is the T-Bill rate, which is the Federal Funds rate of the United States since the return of external bonds causes an increase in the interest rate such as the exchange rate. Additionally, there is evidence of a significant and positive effect in the exchange depreciation on the interest rate. The output variable was defined as the prime cost, that is, the expected result of the estimation.
The structure of the FISPC and its input and output variables are depicted in Fig. 6 and further detailed below.

General structure of fuzzy model.
Once the variables are fixed, it is necessary to define the fuzzy membership functions of the linguistic values in order to facilitate the computation of the degrees of membership for each input value of the variables and the output value. First, the syntax of linguistic values for each variable was defined. For the exchange rate, the Cetes, and T-Bill rates, five labels were defined: “very low”, “low”, “medium”, “high” and “very high”. Their fuzzy membership functions were identified by using the data obtained from the forecast calculation through the econometric models (ARIMA, Moving Average, Winters, and Trend Analysis) [24] with data obtained from institutions such as the Bank of Mexico [25] and Derivatives Market in Mexico [26]. This enabled to establish the range of decisions for each of the variables.
In such a way, for the exchange rate variable in year 2014 a stable level was considered between 12.60 and 13.40, being 13.00 and 13.20 the values that completely belong to this level, considering a universe of discourse in a range of 12.00 to 14.00. Since the historical information of the peso/dollar variation has remained in the same parameters. It is important to clarify that the membership function of the linguistic values “low”, “stable” and “high” was determined based on the forecasting produced by the econometric values (upper data, average data, lower data) and that the labels “very low” and “very high” were determined through querying for historical data. Table 1 shows the membership function definition for each linguistic label of the exchange rate variable and Fig. 7 depicts the trapezoidal functions.

Membership functions for exchange rate.
| Degree of Membership |
|||||
|---|---|---|---|---|---|
| Exchange Rate | Very Low | Low | Stable | High | Very High |
| 12.00 | 1 | 0 | 0 | 0 | 0 |
| 12.10 | 1 | 0 | 0 | 0 | 0 |
| 12.20 | 1 | 0 | 0 | 0 | 0 |
| 12.30 | 0.5 | 0.5 | 0 | 0 | 0 |
| 12.40 | 0 | 1 | 0 | 0 | 0 |
| 12.50 | 0 | 1 | 0 | 0 | 0 |
| 12.60 | 0 | 1 | 0 | 0 | 0 |
| 12.70 | 0 | 0.5 | 0.5 | 0 | 0 |
| 12.80 | 0 | 0 | 1 | 0 | 0 |
| 12.90 | 0 | 0 | 1 | 0 | 0 |
| 13.00 | 0 | 0 | 1 | 0 | 0 |
| 13.10 | 0 | 0 | 1 | 0 | 0 |
| 13.20 | 0 | 0 | 1 | 0 | 0 |
| 13.30 | 0 | 0 | 0.5 | 0.5 | 0 |
| 13.40 | 0 | 0 | 0 | 1 | 0 |
| 13.50 | 0 | 0 | 0 | 1 | 0 |
| 13.60 | 0 | 0 | 0 | 1 | 0 |
| 13.70 | 0 | 0 | 0 | 0.5 | 0.5 |
| 13.80 | 0 | 0 | 0 | 0 | 1 |
| 13.90 | 0 | 0 | 0 | 0 | 1 |
| 14.00 | 0 | 0 | 0 | 0 | 1 |
Membership functions for the exchange rate.
For the input variable CETES interest rate and T-Bill rate, the membership functions are shown in Tables 2 and 3; and depicted in Fig. 8 and Fig. 9 respectively.

Membership functions for Cetes rate.

Membership functions for T-bill rate.
| Degree of Membership |
|||||
|---|---|---|---|---|---|
| Cetes Rate | Very Low | Low | Medium | High | Very High |
| 0.0% | 1 | 0 | 0 | 0 | 0 |
| 0.5% | 1 | 0 | 0 | 0 | 0 |
| 1.0% | 0.5 | 0.5 | 0 | 0 | 0 |
| 1.5% | 0 | 1 | 0 | 0 | 0 |
| 2.0% | 0 | 1 | 0 | 0 | 0 |
| 2.5% | 0 | 1 | 0 | 0 | 0 |
| 3.0% | 0 | 0.5 | 0.5 | 0 | 0 |
| 3.5% | 0 | 0 | 1 | 0 | 0 |
| 4.0% | 0 | 0 | 1 | 0 | 0 |
| 4.5% | 0 | 0 | 1 | 0 | 0 |
| 5.0% | 0 | 0 | 0.5 | 0.5 | 0 |
| 5.5% | 0 | 0 | 0 | 1 | 0 |
| 6.0% | 0 | 0 | 0 | 1 | 0 |
| 6.5% | 0 | 0 | 0 | 1 | 0 |
| 7.0% | 0 | 0 | 0 | 0.5 | 0.5 |
| 7.5% | 0 | 0 | 0 | 0 | 1 |
| 8.0% | 0 | 0 | 0 | 0 | 1 |
Membership functions for the Cetes rate.
| Degree of Membership |
|||||
|---|---|---|---|---|---|
| T-Bill Rate | Very Low | Low | Medium | High | Very High |
| 0.0% | 1 | 0 | 0 | 0 | 0 |
| 0.5% | 0.5 | 0.5 | 0 | 0 | 0 |
| 1.0% | 0 | 1 | 0 | 0 | 0 |
| 1.5% | 0 | 0.5 | 0.5 | 0 | 0 |
| 2.0% | 0 | 0 | 1 | 0 | 0 |
| 2.5% | 0 | 0 | 0.5 | 0.5 | 0 |
| 3.0% | 0 | 0 | 0 | 1 | 0 |
| 3.5% | 0 | 0 | 0 | 0.5 | 0.5 |
| 4.0% | 0 | 0 | 0 | 0 | 1 |
Membership functions for the T-bill rate.
For the output variable, premium cost, the linguistic labels were defined as “very low”, “low”, “medium”, “high” and “very high”. A range of decision of 0 and 1 was proposed, considering the average variation of the Mexican Derivatives Exchange has been registered in the same period. The membership functions for output is shown in the Table 4 and depicted in Fig. 10, respectively.
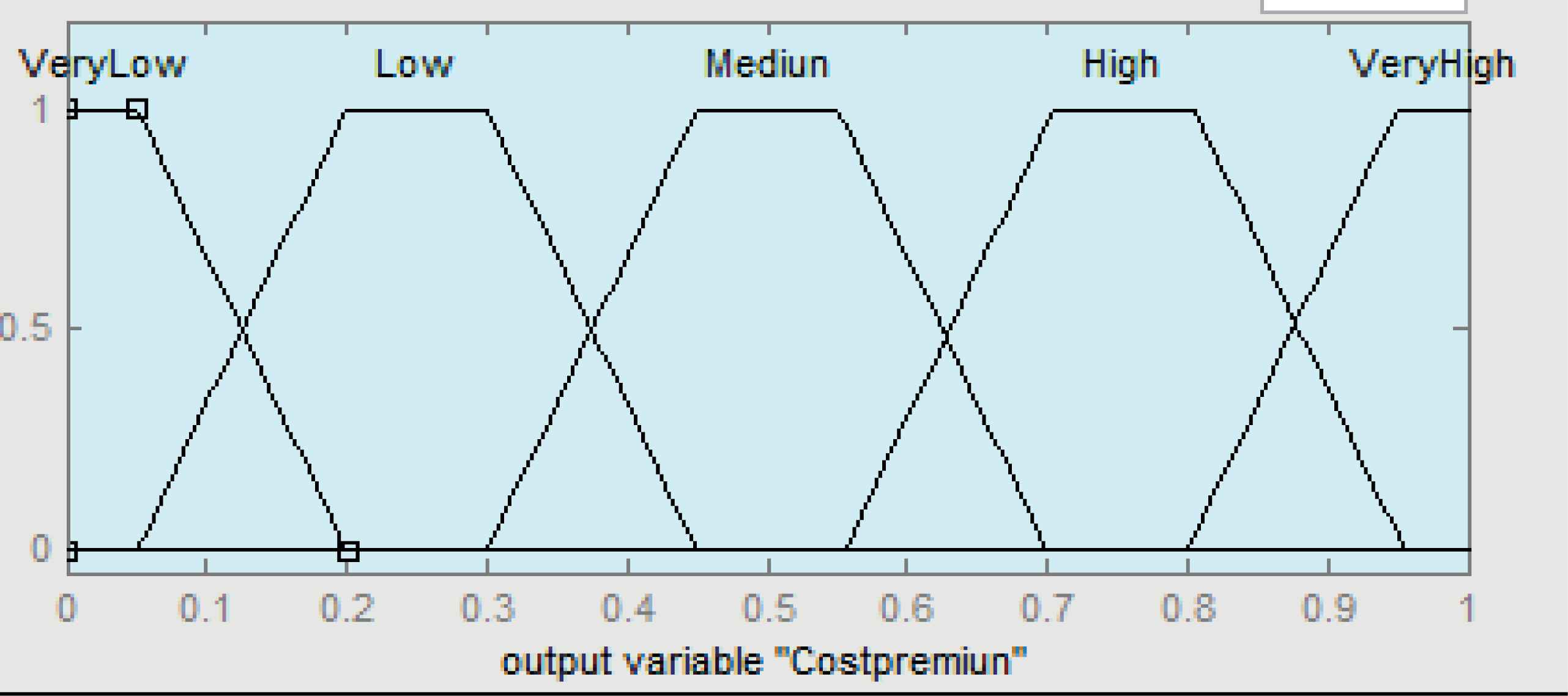
Membership functions for premium cost.
| Degree of Membership |
|||||
|---|---|---|---|---|---|
| Premium | Very | Low | Medium | High | Very |
| 0.00 | 1 | 0 | 0 | 0 | 0 |
| 0.05 | 1 | 0 | 0 | 0 | 0 |
| 0.10 | 0.65 | 0.35 | 0 | 0 | 0 |
| 0.15 | 0.35 | 0.65 | 0 | 0 | 0 |
| 0.20 | 0 | 1 | 0 | 0 | 0 |
| 0.25 | 0 | 1 | 0 | 0 | 0 |
| 0.30 | 0 | 1 | 0 | 0 | 0 |
| 0.35 | 0 | 0.65 | 0.35 | 0 | 0 |
| 0.40 | 0 | 0.35 | 0.65 | 0 | 0 |
| 0.45 | 0 | 0 | 1 | 0 | 0 |
| 0.50 | 0 | 0 | 1 | 0 | 0 |
| 0.55 | 0 | 0 | 1 | 0 | 0 |
| 0.60 | 0 | 0 | 0.65 | 0.35 | 0 |
| 0.65 | 0 | 0 | 0.35 | 0.65 | 0 |
| 0.70 | 0 | 0 | 0 | 1 | 0 |
| 0.75 | 0 | 0 | 0 | 1 | 0 |
| 0.80 | 0 | 0 | 0 | 1 | 0 |
| 0.85 | 0 | 0 | 0 | 0.65 | 0.35 |
| 0.90 | 0 | 0 | 0 | 0.35 | 0.65 |
| 0.95 | 0 | 0 | 0 | 0 | 1 |
| 1.00 | 0 | 0 | 0 | 0 | 1 |
Membership functions for the premium cost.
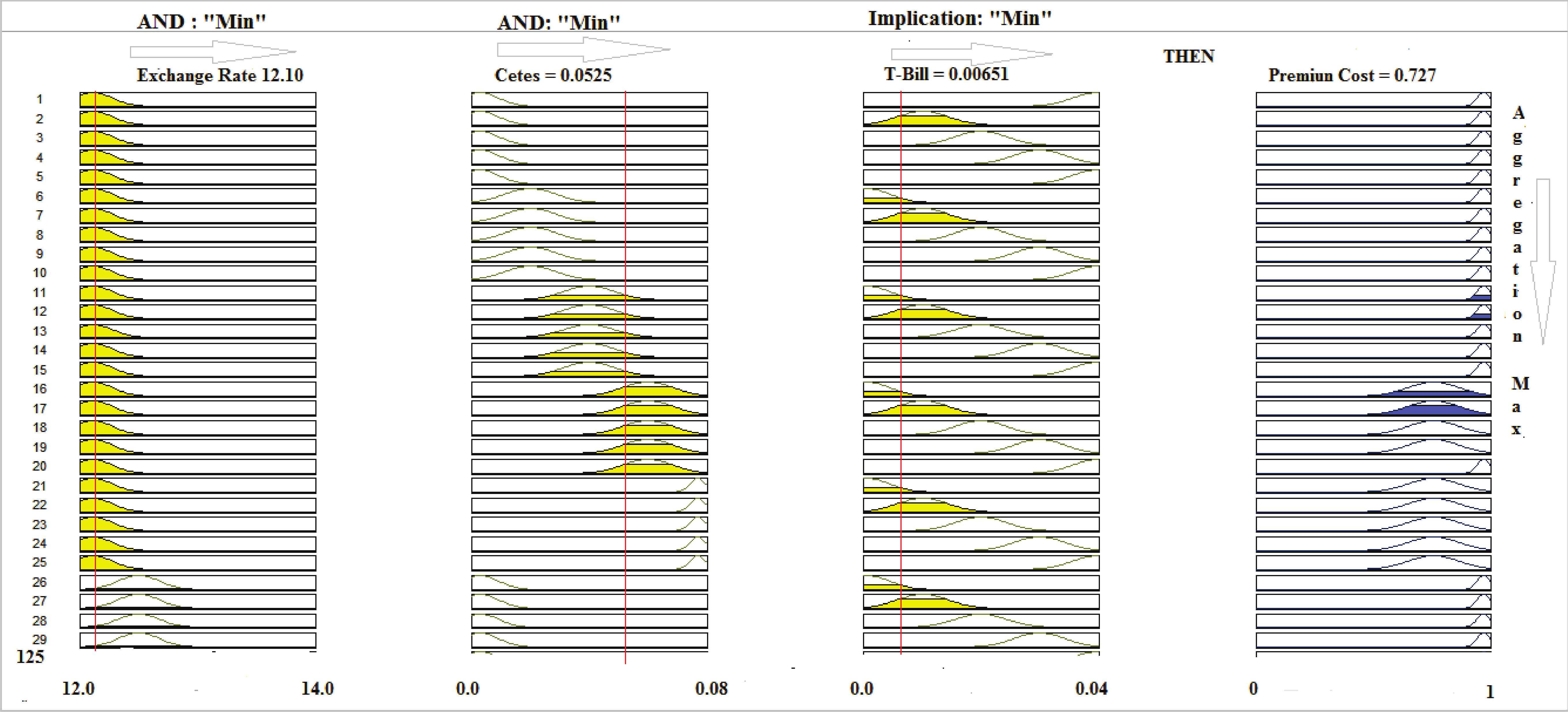
The next step in the development of FISPC is the definition of the “IF-THEN” rules for the fuzzy inference system. These rules will determine the output value by a defuzzification process by means of the centroid method. It is important to emphasize that the number of rules is directly conditioned to the input variables and their respective number of labels. Since five linguistic labels were defined for each of the variables, the possible relations that can be present correspond to 125 rules with the use of “AND” operator. In table 5, the “IF-THEN” rules defined for FISPC are presented in further detail.
| CETES RATE |
||||||||
|---|---|---|---|---|---|---|---|---|
| Muy Bajo | Bajo | Medio | Alto | Muy Alto | ||||
| EXCHANGE RATE | Very Low | T-BILL RATE | Very Low | very high | very high | very high | high | high |
| Low | very high | very high | very high | high | high | |||
| Medium | very high | very high | very high | high | high | |||
| High | very high | very high | very high | high | high | |||
| Very High | very high | very high | very high | very high | high | |||
| Low | Very Low | very high | high | high | medium | medium | ||
| Low | very high | high | high | medium | medium | |||
| Medium | very high | high | high | medium | medium | |||
| High | very high | high | high | medium | medium | |||
| Very High | very high | high | high | medium | medium | |||
| Stable | Very Low | high | high | high | medium | low | ||
| Low | high | high | medium | low | low | |||
| Medium | high | high | medium | low | low | |||
| High | high | high | medium | low | low | |||
| Very High | high | high | medium | low | low | |||
| High | Very Low | medium | medium | low | low | very low | ||
| Low | medium | medium | low | low | very low | |||
| Medium | medium | medium | low | low | very low | |||
| High | medium | medium | low | low | very low | |||
| Very High | high | medium | low | low | very low | |||
| Very High | Very Low | low | low | low | very low | very low | ||
| Low | low | low | low | very low | very low | |||
| Medium | low | low | low | very low | very low | |||
| High | medium | low | low | very low | very low | |||
| Very High | medium | low | low | very low | very low | |||
Rules for fuzzy inference system to estimate the premium cost.
The criteria to define such a set of rules were established based on the particular conditions of the Mexican Market since the established monetary policies have an effect on the economic variables. Interest rates and the exchange rate in Mexico are freely determined by market forces [27]. On the other hand, the exchange rate regimes implemented in Mexico have caused an effect in the prices of the derivatives market that has recently been established in Mexico [28]. In addition, they mention that in the fixed exchange rate regime, there are high levels of capital control and the sample companies are parastatal. In Mexico, where there is trade openness with a flexible exchange rate regime, it is necessary to consider the own conditions of the country´s economy and its effects on the financial markets and as a consequence, its impact in the organizations. Fuzzy theory can become a resource that applied to the economy has the ability to model the behavior of economic agents and incorporate into the analysis the ambiguities and uncertainties of human beings [31]. As a result, investors with a short-term perspective have a different dimension than the long-term perspective investors. For short-term investment, in one day of operation, different events could happen in the financial market in relation to variation of the economic variables, and consequently, the exchange regime variations have an effect on the expected returns by the long-term investor. On the other hand, a free-floating or flexible exchange rate regime such as Mexico which is open to the financial markets, error correction is increased by a model of exchange regime; therefore, error correction takes more than a period for return adjustment. Moreover, the Markow exchange regime model provides evidence to state that the real arbitrage opportunities happen when volatility of returns takes place from one day to another since from one period to another is 36.5% [29]. Hence the importance of having mechanisms that enable investors to establish long-term strategies to cover investments in dollars by means of hedging instruments.
Eventually, the FISPC must obtain an output from the application of the rules to the input data, insofar they are subject to the implication method to establish the degrees of membership; later, the fuzzy sets are grouped in one fuzzy set that is defuzzified by a defuzzification process which will obtain a crisp value with the different degrees of membership of each variable. To show relationships graphically are used the tool Surface Matlab Toolbox 7.1. Fig. 11 show as the premium cost increases when the exchange rate and the Cetes interest rates decrease. Similarly, it can be observed that as the T-Bill rate increases and the Cetes rate decreases, then the premium cost decreases.

Relationships between exchange rate, Cetes rate and the cost of the premium expected.
4. Experimental analysis
With the purpose of comparing the estimates obtained from FISPC with Black-Scholes (B-S) model, data were collected from the available information on premium cost quarterly reports produced by the Mexican Derivatives Exchange (MexDer). Table 6, shows the results obtained through the FISPC in comparison to the real results obtained from MexDer and the results obtained from the estimates done through the theoretical B-S model.
| Exchange Rate | FISPC | B-S | Mex-Der |
|---|---|---|---|
| 12.00 | 0.9320 | 0.2451 | 0.9780 |
| 12.10 | 0.9200 | 0.2269 | 0.9720 |
| 12.20 | 0.9060 | 0.2233 | 0.9610 |
| 12.30 | 0.8280 | 0.2587 | 0.9440 |
| 12.40 | 0.7580 | 0.2285 | 0.9210 |
| 12.50 | 0.7500 | 0.2427 | 0.8910 |
| 12.60 | 0.7040 | 0.2398 | 0.8500 |
| 12.70 | 0.6450 | 0.2440 | 0.7980 |
| 12.80 | 0.6840 | 0.2471 | 0.7380 |
| 12.90 | 0.5880 | 0.2690 | 0.6720 |
| 13.00 | 0.5750 | 0.2711 | 0.5990 |
| 13.10 | 0.4870 | 0.3055 | 0.5250 |
| 13.20 | 0.4180 | 0.3125 | 0.4520 |
| 13.30 | 0.3590 | 0.3052 | 0.3840 |
| 13.40 | 0.3730 | 0.2499 | 0.3240 |
| 13.50 | 0.2900 | 0.2686 | 0.2710 |
| 13.60 | 0.2500 | 0.3141 | 0.2270 |
| 13.70 | 0.2190 | 0.2980 | 0.1910 |
| 13.80 | 0.1700 | 0.3118 | 0.1630 |
| 13.90 | 0.1860 | 0.3842 | 0.1390 |
| 14.00 | 0.1130 | 0.3998 | 0.1210 |
Compiled data obtained by the B-S theoretical, MexDer and FISPC.
4.1 Analysis of results
The analysis of variance (Anova) with Minitab software was performed for determining the similarity of the models, it can be inferred that hypothesis test F (Fisher) a value in Ftest of 9.27 is obtained and in the Ftable 3.150. Therefore, there are differences in determining the premium cost for each of the models analyzed; however, the model that has the greatest approximation to the derivatives market is the FISPC model, as it can be observed in Fig. 12.

Comparative analysis of the values obtained in the B-S theoretical, MexDer and FISPC.
From the results, it can be established that the FISPC model shows an expected behavior in comparison to MexDer; showing a more efficient approximation that the theoretical B-S model. As it can be observed in Fig. 12, there is a high correlation between the FISPC and the derivatives market, as a result, it is inferred that the Mamdani application to estimate the premium cost of an exchange option is an alternative tool that can be used by the decision makers. The application of fuzzy logic allows decision- making with estimated values under incomplete or uncertain information; this is especially useful in risk assessment [18]. Fuzzy inference system considers subjective assessments, which are approximated to values accurate applying to economic variables [31].
5. Conclusion
This paper we introduced a model for estimating premium cost of option exchange using Mamdani inference system that captures more accurately the behavior of the financial variables in the financial markets and considers the opinions of experts; in comparison with quantitative models. Presents fuzzy logic as a methodology and alternative tool for pose and solve the problems of decision theory in economy.
Our FISCP model allows a better approximation on the estimating of premium cost of an option exchange in comparison with traditional B-S model. FISCP uses Mamdani inference system in the economic variables: exchange rate, domestic interest rate (Cetes), and foreign interest rate (T-Bill). Results show the application of fuzzy logic as an alternative for financial risk management in the face of volatility of the financial markets which has a direct impact on the premium cost of an option exchange. Our model also presents an alternative for obtaining different possibilities at the moment of exercising the option; allowing chief executive can optimize decision-making to minimize risk and obtain a higher index of profitability for organizations.
FISCP experimental results demonstrated that with the application of fuzzy logic, the degree of uncertainty can be reduced better than S-B; given that are obtained better results at the time that option can be exercised. Thereby, stand out significant difference between the obtained values with our model and the obtained values with B-S model and derivatives market. FISCP allows future research considering other variables in the study of financial risk and other derivative instruments as futures, interest rate options, warrants, etc. using computing with words for the analysis of risk decisions under uncertainty.
Acknowledgments
The research is supported partially by the Conacyt Mexico (N- 238016) and the Research Funds provided of the University Oldenburg in collaboration with Eureka st.
References
Cite this article
TY - JOUR AU - M. Muñoz AU - E. Miranda AU - PJ. Sánchez PY - 2017 DA - 2017/01/01 TI - A Fuzzy System for Estimating Premium Cost of Option Exchange Using Mamdani Inference: Derivatives Market of Mexico JO - International Journal of Computational Intelligence Systems SP - 153 EP - 164 VL - 10 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.2017.10.1.11 DO - 10.2991/ijcis.2017.10.1.11 ID - Muñoz2017 ER -
