1. INTRODUCTION

In our real life situations, we see that some objects are related by some relations. For example, in a city, places are connected by trum ways. There may have a problem to construct the transportation roads so that there is minimum number of ways to move from one place to another place. These type of problems can easily be handled by considering the objects as nodes (or, vertices) and trum ways are the links (or, edges). This one-to-one representation is called the graph. The concept of graph theory was first introduced by Euler in his paper “Seven bridges of Königsberg” (1736). A suitable mathematical model is needed when fuzziness arises in the kind of objects or that in the relationship among the objects. Rosenfeld [1] first developed the crisp graph to fuzzy graph by introducing fuzzy relation in fuzzy sets which was first introduced by Zadeh [2]. Since then, researchers are delve into field of fuzzy graph theory and many of the real phenomena has been expressed in terms of fuzzy model (see [3]). Thus the field of fuzzy graph theory is flourishing it can handle the vaguenesses in real-world. Several real-world problems like human cardiac function, fuzzy neural network, routing problem, traffic light problem, time table scheduling, etc. can be nicely expressed using fuzzy graph model.

After Rosenfeld, fuzzy graph theory developed with many variations in fuzziness. In 1971, Zadeh [4] introduced the concept of interval-valued fuzzy sets (IVFSs) to generalize the fuzzy sets [2] in which the membership function describes to return interval numbers instead of classical numbers. It is more strong enough to consider the uncertainty cases than the traditional fuzzy sets as interval numbers are considered instead of classical numbers. The interval-valued fuzzy graph (IVFG) theory studies the generalized class of fuzzy graphs with IVFSs with interval-valued fuzzy relations. Therefore, it has more area of applications such as fuzzy control, approximate reasoning, medical diagnosis, intelligent control, multivated logic, etc. Talebi and Rashmanlou [5] studied isomorphism on IVFG. Several theorems and the properties of Complete IVFGs are studied by Rashmanlou and Jun in their literature [6]. Pal and Rashmanlou [7] have studied another variation of IVFG namely, irregular IVFG in which the adjacent vertices have distinct degrees. Antipodal IVFG is an another classification of IVFG which is introduced by Rashmanlou and Pal [8]. They also have defined a new type of IVFG – Balanced IVFG in the literature [9]. Bipolar fuzzy graphs are studied by Rashmanlou et al. [10]. Pramanik et al. [11] have extended the fuzzy competition graph to a bipolar fuzzy competition graph so that it can solve several real-world problems. Samanta et al. [12] have represented and analyzed the competitions among the participants in social networks. Pramanik et al. [13] have introduced the fuzzy ϕ-tolerance competition graphs. In 2016, concept of planarity is first introduced in IVFG by Pramanik et al. [14]. In this year, they also have extended the idea of fuzzy ϕ-tolerance competition graphs in IVFGs [15]. They also have considered certain threshold in each of fuzzy vertices and introduced interval-valued fuzzy threshold graph [16]. Bipolar fuzzy planar graphs have been extensively studied by Pramanik et al. [17] in 2018. They have shown its uses in image shrinking with an arbitrary graph model. In 2020, fuzzy competition graphs have been extended by Pramanik et al. [11] and given an idea of application to manufacturing industries. In literature [18], a new type of measurements in IVFGs are introduced by Pramanik et al. Several algorithmic approach to find the fuzzy shortest path in an interval-valued fuzzy hypergraphs is presented by Pramanik and Pal [19]. Also, the all-pairs shortest path problem for general network is investigated in [20]. For further definitions, terminologies and applications the reader may read the newly published book by Pal et al. [21]. For more details of fuzzy graphs, look in [1,22–29].

In today's communication networks, one person has friends (or buddies) and it is assumed that each friend in his friend list is known to each other. This type of network in graph modelling is called the clique (See Figure 1). The maximal clique is a clique with no proper subset which is also a clique. The maximal clique with maximum number of nodes (vertices) is the maximum clique. In many problems such as circuit design, transprotation, human brain analysis, artificial intelligence etc., it is an important task to find the set of maximum number of nodes (vertices) each of which are related to each other. Motivating from this idea, IVFQs and IVFQCs of IVFGs are studied in this article. It is also known that, if all the vertices of any subgraph of a graph forms a clique, then the subgraph is complete. But this conceptual phenomena is not intact in fuzzy graph according to the definition of fuzzy cliques introduced by Nair and Cheng [30]. In this paper, we have modified the definition of IVFQ and IVFQC given by Nair and Cheng and found a new dimension of work. We have built a connection between crisp concept and interval-valued fuzzy concept. The definition of fuzzy clique is modified so that every complete fuzzy subgraph is a fuzzy clique and then the fuzzy cliques and fuzzy clique covers are generalized for IVFGs.

Figure 1

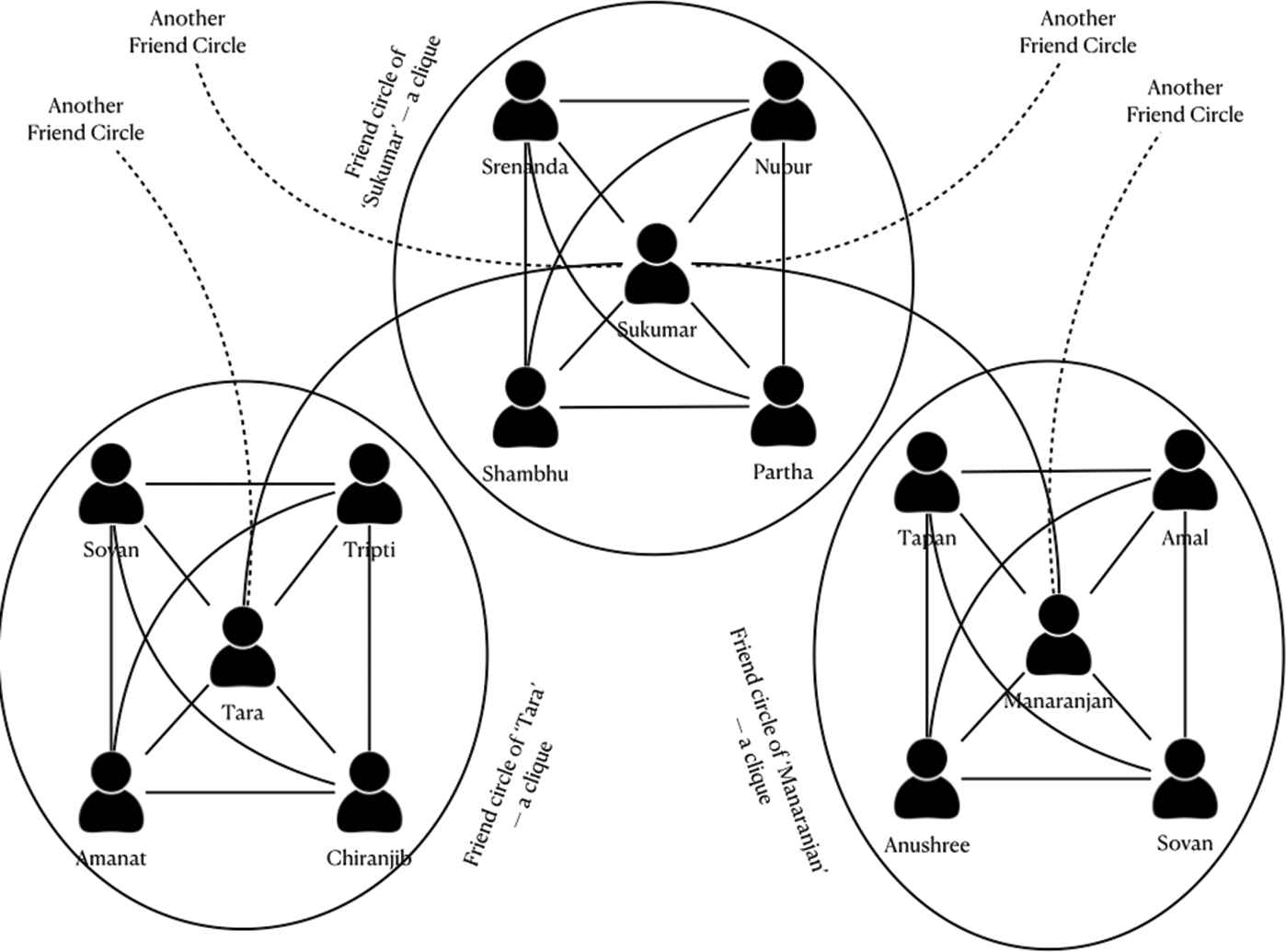
An example of communication network consisting of cliques.

2. PRELIMINARIES

A graph Z=(U,T) includes a set denoted by U, or by U(Z) and a collection T, or T(Z), of un-ordered pair (u,v) of elements from the set U. Each element of U is called a vertex, and each element of T is called an edge.

An edge that connects vertices vi and vj in U is denoted by (vi,vj). Two vertices vi and vj in U are adjacent if (vi,vj)∈T. A walk in Z is a sequence of vertices and edges of the form v1, (v1,v2), v2, (v2,v3), …,(vn−1,vn), vn which is denoted by v1v2v3⋯vn. A path is a walk where none of the vertices is repeated. The walk where v1=vn(n≥3) and vi≠vj for any i,j∈ n − 1 is called cycle. The length of a path or a cycle is the number of its edges.

In a crisp graph J, a set of pairwise adjacent vertices is a clique. A clique is said to be a maximal clique if the set consisting of the clique is not a subset of any other clique set.

A clique cover of a graph J is a clique induced by all the vertices of the graph J. The minimum number of cliques in a graph J required to cover the graph J is called the clique cover number and is denoted by cc(J).

The union of two graphs Z=(UZ,TZ) and H=(UH,TH) is the graph Z∪H=(UZ∪UH,TZ∪TH).

A fuzzy set P on a set L is defined by a function P:L→[0,1] and the function is called membership function. The mapping R:L×M→[0,1] is said to be fuzzy relation. For any two fuzzy sets Q and R on L, Q is said to be the fuzzy subset of R i.e., Q is included in R, denoted by Q⊆R, if and only if Q(p)≤R(p) for all p∈P.

A family of fuzzy sets is denoted by ℱ(L) defined on L and ℱ(L×M) be the family of fuzzy relations defined on L×M.

Let us consider a fuzzy set σ and a fuzzy relation μ be such that μ≤σ(u)∧σ(v) for all u,v∈U. Then the tuple J=(U,σ,μ) is called the fuzzy graph. The fuzzy set σ is called the fuzzy vertex set of J and the fuzzy relation μ is called the fuzzy edge set of J.

When the fuzzy relation μ is symmetric then the fuzzy graph is said to be undirected fuzzy graph otherwise the fuzzy graph is said to be directed.

Throughout this paper, undirected fuzzy graphs are considered and also there is no loops i.e., μ(u,u)=0 for all u∈U.

The crisp graph J∗=(U,σ∗,μ∗), where σ∗={u∈U:σ(u)>0} and μ∗={(u,v)∈U×U:μ(u,v)>0}.

Let us consider a mapping μQ:L→[0,1]×[0,1] then the fuzzy set μQ on L is said to be the IVFS if and only if μQ−(u)≤μQ+(u) where μQ(u)=[μQ−(u),μQ+(u)] for all u∈L.

Let ℱ={Q1,Q2,⋯,Qn} be a finite family of interval-valued fuzzy subsets on a set L. The fuzzy intersection of two IVFSs Q1 and Q2 is an IVFS defined by

Let ℱ={Q1,Q2,⋯,Qn} be the finite collection of IVFSs on a set L. The fuzzy intersection of two IVFSs Q1 and Q2 is an IVFS defined by

Let Q={[μQ−(u),μQ+(u)]:u∈U} be a fuzzy set and ℛ={[μℛ−(u,v),μℛ+(u,v)]:(u,v)∈U×U} defined on U together forms an IVGF. Here the fuzzy set Q is said to be the interval-valued fuzzy vertex set (IVFVS) and the fuzzy set ℛ is said to be the interval-valued fuzzy edge set (IVFES) of the IVFG. An edge (u,v), u,v∈U in an IVFG is said to be interval-valued strong if I(u,v)−=μℛ−(u,v)min{μQ−(u),μQ−(v)}≥0.5 and I(u,v)+=μℛ+(u,v)min{μQ+(u),μQ+(v)}≥0.5 otherwise the edge is called interval-valued weak. The strength of an edge (u,v) is assumed by I(u,v)=[I(u,v)−,I(u,v)+]. An edge is said to be nontrivial if I(u,v)−>0. An IVFG Z=(U,Q,ℛ) is said to be an interval-valued fuzzy strong graph if and only if I(u,v)−=μℛ−(u,v)min{μQ−(u),μQ−(v)}≥0.5 and I(u,v)+=μℛ+(u,v)min{μQ+(u),μQ+(v)}≥0.5, ∀ (u,v)∈U×U.

The underlying graph of the IVFG Z=(U,Q,ℛ) is the crisp graph Z∗=(U,Q∗,ℛ∗), where Q∗={u∈U:μQ−(u)>0} and ℛ∗={(u,v)∈U×U:μℛ−(u,v)>0}. An interval-valued fuzzy digraph (IVFDG) Z→=(U,Q,ℛ→) is an IVFG where the fuzzy relation ℛ→ is antisymmetric.

An IVFG Z=(U,Q,ℛ) is said to be complete IVFG if μℛ−(u,v)=min{μQ−(u),μQ−(v)} and μℛ+(u,v)=min{μQ+(u),μQ+(v)}, ∀u,v∈U. An IVFG is said to be bipartite if the vertex set U can be partitioned into two sets U1 and U2 such that μℛ+(u,v)=0 if u,v∈U1 or u,v∈U2 and μℛ+(v1,v2)>0 if v1∈U1 (or U2) and v2∈U2 (or U1).

An IVFG ℋ=(U′,Q′,ℛ′) is called an interval-valued fuzzy subgraph (IVFSG) of the IVFG Z=(U,Q,ℛ) induced by U′ if U′⊆U, μQ′−(u)=μQ−(u) and μQ′+(u)=μQ+(u) for all u∈U′ and μℛ′−(u,v)=μℛ−(u,v) and μℛ′+(u,v)=μℛ+(u,v) for all u,v∈U′.

An IVFSG ℋ=(U′,Q′,ℛ′) induced by Q′ is the maximal IVFSG of Z=(U,Q,ℛ) which has the IVFVS Q′ and the IVFES ℛ′ be such that μℛ′−(u,v)=μQ′−(u)∧μQ′−(v)∧μℛ−(u,v) and μℛ′+(u,v)=μQ′+(u)∧μQ′+(v)∧μℛ+(u,v) for all u,v∈U.

An IVFG is called an interval-valued fuzzy cycle (IVFC) if and only if it contains more than one weakest edge (i.e., there is no unique (u,v)∈ℛ∗ such that μℛ−(u,v)=∧{μℛ−(u,v) | (u,v)∈ℛ∗}) and is a cycle.

An IVFSG IVFSG ℋ=(U′,Q′,ℛ′) is Z=(U,Q,ℛ) is an IVFQ if ℋ∗ is a clique and each cycle in ℋ is an IVFC.

2.2. IVFQs in IVFGs

In graph theory, a clique induces a complete subgraph. However, the IVFSG induced by an IVFQ may not be complete.

Example 1.

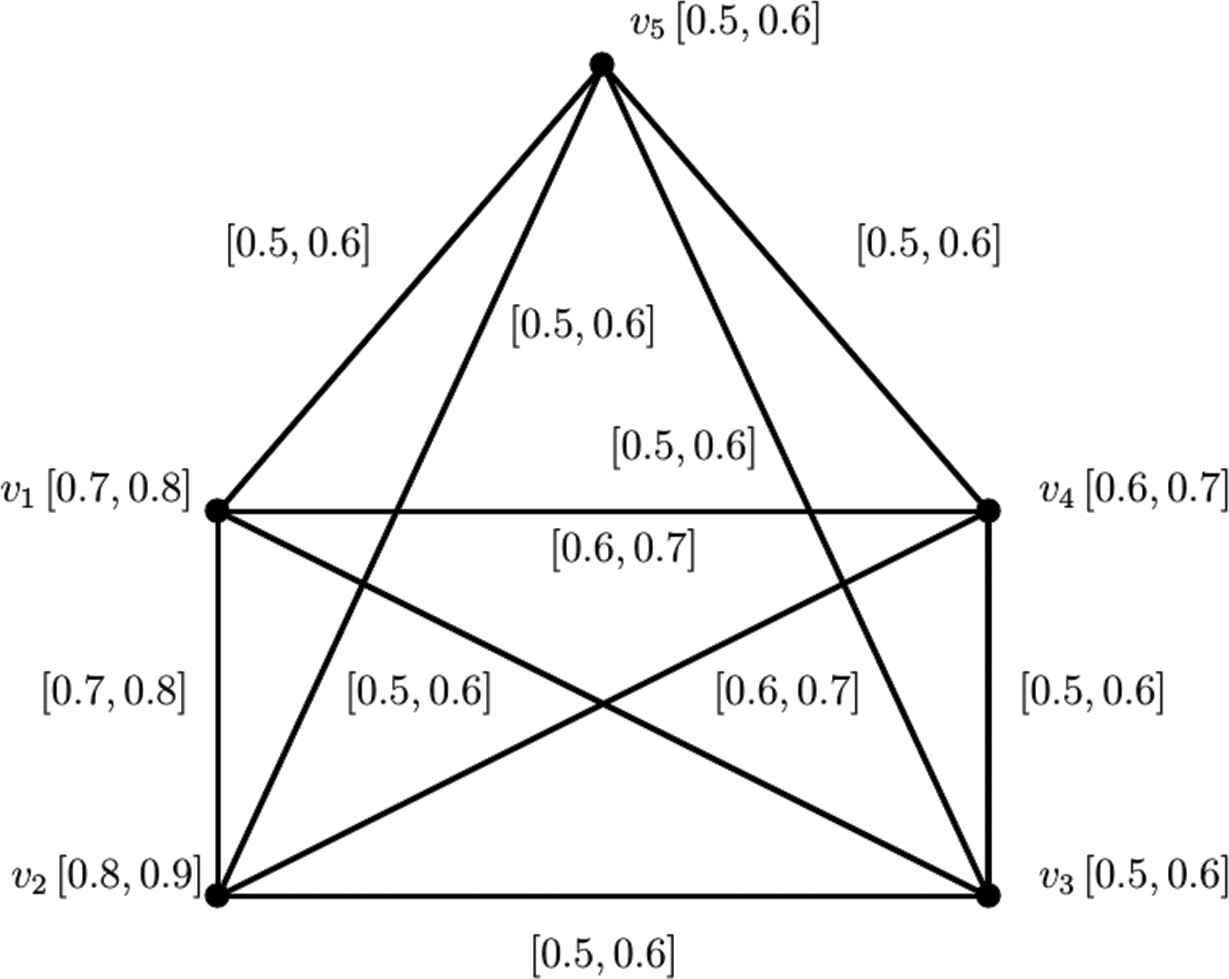
Consider the IVFG Z=(U,Q,ℛ) where U={v1,v2,v3,v4,v5} be the vertex set and Q being the IVFS on U with μQ(v1)=μQ(v2)=μQ(v3)=μQ(v4)=μQ(v5)=[1,1] and ℛ being the interval-valued fuzzy relation on the set U×U whose definition is given in the Table 2:

e∈U×U	(v1,v2)	(v1,v3)	(v1,v4)	(v1,v5)	(v2,v3)	(v2,v4)	(v2,v5)
μℛ(e)	[0.5,0.6]	[0.5,0.6]	[0.6,0.7]	[0.5,0.6]	[0.8,0.9]	[0.6,0.7]	[0.5,0.6]
e∈U×U	(v3,v4)	(v3,v5)	(v4,v5)
μℛ(e)	[0.7,0.8]	[0.5,0.6]	[0.5,0.6]

Table 2

Membership values for the fuzzy edges of the graph Z=(U,Q,ℛ) of Example 1.

The diagrammatical representation of this graph is shown in Figure 2. The IVFSG induced by an interval-valued fuzzy subset Q′=v1[0.7,0.8],v2[1,1],v3[0.7,0.8],v4[0.8,0.9],v5[0.6,0.7]. The diagrammatical representation of this graph is shown in Figure 3. Obviously, this is not a complete IVFSG.

Figure 2

An example of a fuzzy graph Z=(U,Q,ℛ).

Figure 3

An interval-valued fuzzy subgraph (IVFSG) which is fuzzy clique but not complete.

Now, definition of IVFQ should be so modified that the IVFSG induced by each fuzzy clique is complete. This complete IVFQ is known as complete IVFQ.

Definition 4.

(Complete IVFQ) In an IVFG Z=(U,Q,ℛ), a subset Q′ of Q is called a complete IVFQ if the fuzzy subgraph induced by Q′is a complete IVFG.

Now, we see an example of a complete IVFQ as a subgraph of the graph shown in Figure 2.

Example 2.

Consider an IVFSG of the graph in Example 1 induced by Q′=v1[0.7,0.8], v2[0.8,0.9], v3[0.5,0.6], v4[0.6,0.7], v5[0.5,0.6] which is shown in Figure 4. This graph is a complete IVFG and hence the interval-valued fuzzy subset Q′ of Q is a complete IVFQ.

Figure 4

An example of a complete interval-valued fuzzy cliques (IVFQ) of the graph of Figure 2.

Theorem 1.

Each complete IVFSG is an IVFQ.

Proof.

Let ℋ=(U,Q′,ℛ′) be a complete IVFSG of the graph Z=(U,Q,ℛ). Since ℋ is complete then, μℛ−(u,v)=min{μQ−(u),μQ−(v)} and μℛ+(u,v)=min{μQ+(u),μQ+(v)}, ∀u,v∈U. This shows that if μQ−(u),μQ−(v),μQ+(u),μQ+(v)>0 then μℛ−(u,v),μℛ+(u,v)>0. Then the crisp graph ℋ∗ is complete and therefore, for any cycle v1v2v3v1 (v1,v2,v3∈Q∗) of length 3 in ℋ,

μℛ−(v1,v2)=min{μQ−(v1),μQ−(v2)}(1)

μℛ−(v2,v3)=min{μQ−(v2),μQ−(v3)}(2)

μℛ−(v3,v1)=min{μQ−(v3),μQ−(v1)}(3)

Now, without any loss of generality, suppose that μQ−(v1)=min{μQ−(v1),μQ−(v2),μQ−(v3)}

Then from (1), (3) we have, μℛ−(v1,v2)=μQ−(v1)=min{μQ−(v3),μQ−(v1)}. This shows that the graph ℋ has more than one weakest edges. Therefore, every cycle of length 3 is an IVFC. Hence, ℋ is an IVFQ.

Corollary 1.

The IVFSG induced by a complete IVFQ is an IVFQ.

Proof.

By the definition of complete IVFQ we have the IVFSG induced by a complete IVFQ is complete. Then by Theorem 1, it is an IVFQ.

Theorem 2.

If IVFQ is a perfect interval-valued fuzzy strong then it is complete.

Proof.

Let ℋ=(U,Q,ℛ) be an IVFQ as well as perfect interval-valued fuzzy strong graph. Since, ℋ is an IVFQ then, ℋ∗ is a clique. Then for any u,v∈Q∗, (u,v)∈ℛ∗. Again ℋ is perfect interval-valued fuzzy strong then it follows that μℛ−(u,v)=min{μQ−(u),μQ−(v)}, ∀ (u,v)∈ℛ∗. Therefore, μℛ−(u,v)=min{μQ−(u),μQ−(v)}, ∀ u,v∈Q∗. Hence, the IVFQ is complete.

Theorem 3.

In an IVFG Z=(U,Q,ℛ), a subset Q′ of Q is a complete IVFQ if and only if μℛ−(u,v)≥min{μQ′−(u),μQ′−(v)} and μℛ+(u,v)≥min{μQ′+(u),μQ′+(v)}∀ u,v∈Q∗ and u≠v.

Proof.

First consider that Q′ is a complete IVFQ in Z=(U,Q,ℛ) and ℋ=(U,Q′,ℛ′) is the IVFSG induced by Q′. By Corollary 1, ℋ is a complete IVFSG. Then, we have min{μQ′−(u),μQ′−(v)}=μℛ′−(u,v)=minμQ′−(u),μQ′−(v),μℛ−(u,v)≤μℛ−u,v for all u,v∈Q∗ and minμQ′+(u),μQ′+(v)=μℛ′+(u,v)=minμQ′+(u),μQ′+(v),μℛ+(u,v)≤μℛ+u,v for all u,v∈Q∗ and u≠v.

Conversely, consider that Q′ is a subset of Q such that μℛ−(u,v)≥min{μQ′−(u),μQ′−(v)} and μℛ+(u,v)≥min{μQ′+(u),μQ′+(v)}∀ u,v∈Q∗ and u≠v. Since ℋ=(U,Q′,ℛ′) is the IVFSG induced by Q′, we have μℛ′−(u,v)=minμQ′−(u),μQ′−(v),μℛ−(u,v)=minμQ′−(u), μQ′−(v)} and μℛ′+(u,v)=minμQ′+(u),μQ′+(v),μℛ+(u,v)=minμQ′+(u),μQ′+(v)∀u,v∈Q∗ and u≠v. Hence, ℋ is complete IVFSG of the graph Z.

The following corollaries are two consequences of Theorem 3.

Corollary 2.

Q′ be a complete IVFQ in Z=(U,Q,ℛ). Then for each t∈(0,1], Q′t is a clique in Zt.

Proof.

Since, Q′ is a complete IVFQ in Z, then from Theorem 3, we have μℛ−(u,v)≥min{μQ′−(u),μQ′−(v)} and μℛ+(u,v)≥min{μQ′+(u),μQ′+(v)}∀ u,v∈Q∗ and u≠v. For each t∈(0,1], Q′t={u∈U:μQ′−(u)≥t} which implies that μℛ−(u,v)≥min{μQ′−(u),μQ′−(v)}≥t. Therefore (u,v)∈ℛt. Hence Q′t is a clique in Zt.

Corollary 3.

Let Q′ be a complete IVFQ in Z=(U,Q,ℛ). Then each nonempty subset Q″ of Q′ is a complete IVFQ in Z.

Proof.

This is immediate from Theorem 3 since, μQ″−(u)≤μQ′−(u) and μQ″+(u)≤μQ′+(u)∀u∈U.

In the following, we shall give another characterization of a complete IVFQ. For an IVFG Z=(U,Q,ℛ), define an n×n interval-valued fuzzy matrix MZ by

(MZ)ij={[μQ−(vi),μQ+(vi)],i=j[μℛ−(vi,vj),μℛ+(vi,vj)],i≠j.

For a subset Q′ of Q of the IVFG Z=(U,Q,ℛ), define an n×1 interval-valued fuzzy vector UQ by

(UQ)={[μQ′−(vi),μQ′+(vi)],vi∈(Q′)∗,[0,0],vi∉(Q′)∗

Let χZ={ℒ=([u1,v1][u2,v2]⋮[un,vn]):ui,vi∈[0,1](i=1,2,…,n)and ℒ⊙ℒT≤MZ}. Then we have the follwing theorem.

Theorem 4.

If Q′ be a complete IVFQ of an IVFG Z=(U,Q,ℛ), then UQ′∈χZ. Conversely, for any ℒ=([u1,v1][u2,v2]⋮[un,vn])∈χZ, the IVFS Q′ with μQ′−(vi)=ui and μQ′+(vi)=vi for all i∈n_ is a complete IVFQ.

Proof.

Let Q′ be a complete IVFQ in Z. Then from Theorem 3 it follows that (UQ′⊙UQ′T)ij=min{(UQ′)i,(UQ′)j}=[min{μQ′−(vi),μQ′−(vj)}, min{μQ′+(vi),μQ′+(vj)}]≤[μℛ−(vi,vj),μℛ+(vi,vj)](MZ)ij for any i,j∈n_ with i≠j and (UQ′⊙UQ′T)ii=min(UQ′)i, (UQ′)i=[min{μQ′−(vi),μQ′−(vi), min{μQ′+(vi),μQ′+(vi)}]≤[μℛ−(vi,vi),μℛ+(vi,vi)]=(MZ)ii for any i∈n_. Therefore, UQ′∈χZ.

Conversely, let ℒ=([u1,v1][u2,v2]⋮[un,vn])∈χZ and an IVFS Q′ be such that μQ′−(vi)=ui and μQ′+(vi)=vi∀i∈n_. Since, μQ′(vi)=[ui,vi]≤(MZ)ii=μQ(vi) for all i∈n_, we have Q′⊆Q. Then from Theorem 3, Q′ is a complete IVFQ. Hence the result follows.

The following example illustrates Theorem 4.

Example 3.

Let us consider the IVFG Z=(U,Q,ℛ) and the complete IVFQ Q′ in Example 2. Then we have

MZ=([1,1][0.8,0.9][0.5,0.6][0.6,0.7][0.5,0.6][0.8,0.9][1,1][0.8,0.9][0.6,0.7][0.5,0.6][0.5,0.6][0.8,0.9][1,1][0.7,0.8][0.5,0.6][0.6,0.7][0.6,0.7][0.7,0.8][1,1][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][1,1])

and UQ′=([0.7,0.8][0.8,0.9][0.5,0.6][0.6,0.7][0.5,0.6]). Then it can be easily verified that

UQ′⊙(UQ′)T=([0.7,0.8][0.7,0.8][0.5,0.6][0.6,0.7][0.5,0.6][0.7,0.8][0.8,0.9][0.5,0.6][0.6,0.7][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.6,0.7][0.6,0.7][0.5,0.6][0.6,0.7][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6][0.5,0.6])≤MZ.

This shows that UQ′∈χZ.

Corollary 3 states that every nonempty subset of a complete IVFQ is complete IVFQ. This gives a clue of having maximal and maximum complete IVFQ. Now, we give the definitions of maximal and maximum complete IVFQ.

Definition 5.

(Maximal and maximum complete IVFQ) A complete IVFQ Q″ in an IVFG Z=(U,Q,ℛ) is said to be maximal if there is no complete IVFQ Q′ in Z such that Q″⊂Q′. A maximal complete IVFQ Q″ is maximum if it posses the largest possible cardinality of the crisp set (Q″)∗.

Using Theorem 4, we can characterize the maximal complete IVFQs.

Theorem 5.

In an IVFG Z=(U,Q,ℛ), an interval-valued fuzzy subset Q″ of Q is a maximal complete IVFQ if and only if UQ″ is a maximal element in χZ.

Proof.

By Theorem 4, Q″ is a complete IVFQ if and only if UQ″∈χZ. Furthermore, if Q″ is maximal, then UQ″ is maximal in χZ and vice-versa. Hence, the result follows.

Theorem 6.

Let Q′ be a maximal complete IVFQ in Z=(U,Q,ℛ). Then ⋀u∈(Q′)∗μQ′−(u)=⋀v,z∈(Q′)∗μℛ−(v,z).

Proof.

Let us consider that the set Q′ is a complete IVFQ in the IVFG Z=(U,Q,ℛ). Then by Theorem 3, we have μℛ−(u,v)≥min{μQ′−(u),μQ′−(v)} and μℛ+(u,v)≥min{μQ′+(u),μQ′+(v)} for any u,v∈(Q′)∗. Therefore, ⋀u∈(Q′)∗μQ′−(u)≤⋀v,z∈(Q′)∗μℛ−(v,z). Let μQ′−(vk)=⋀u∈(Q′)∗μQ′−(u) and μℛ−(vi,vj)=⋀v,z∈(Q′)∗μℛ−(v,z) and μQ′+(vk)=⋀u∈(Q′)∗μQ′+(u) and μℛ+(vi,vj)=⋀v,z∈(Q′)∗μℛ+(v,z). Now, we prove that μQ′−(vk)=μℛ−(vi,vj) and the similar proof can be shown for μQ′+(vk)=μℛ+(vi,vj). If possible let μQ′−(vk)≠μℛ−(vi,vj). Then, μQ′−(vk)<μℛ−(vi,vj) as the other case μQ′−(vk)>μℛ−(vi,vj) does not hold in the fuzzy graph. Now, define an IVFS Q″ such that μQ″−(u)=μQ′−(u), ∀u(≠vk)∈U and μQ″−(vk)=μℛ−(vi,vj). Then it is obvious that Q′⊂Q″⊆Q, since, μQ″−(vk)=μℛ(vi,vj)⋀v,z∈(Q′)∗μℛ−(v,z)≤μℛ−(vk,z)≤μQ−(vk)∧μQ−(z)≤μQ−(vk) for any z∈(Q′)∗. Now, it is to be shown that Q″ is a complete IVFQ, i.e., μQ″−(v)∧μQ″−(z)≤μℛ−(v,z) for any v,z∈(Q′)∗. For all v,z∈U with v≠vk,z≠vk, μQ″−(v)∧μQ″−(z)=μQ′−(v)∧μQ′−(z)≤μℛ−(v,z). Otherwise, without any loss of generality, let, vk=v, then μQ″−(v)∧μQ″−(z)=μQ′−(vk)∧μQ′−(z)μℛ−(vi,vj)∧μQ′−(z)≤μℛ−(vi,vj)⋀u,v∈(Q′)∗μℛ−(u,v)≤μℛ−(v,z). Therefore, Q″ is a complete IVFQ, which contradicts the assumption that Q′ is maximal. Thus ⋀u∈(Q′)∗μQ′−(u)=⋀v,z∈(Q′)∗μℛ−(v,z) and hence the result follows.

Corollary 4.

Let Q′ be a maximal complete IVFQ in the IVFG Z=(U,Q,ℛ) and ℋ=(U,Q′,ℛ′) be the IVFSG induced by Q′ and ⋀u,v∈(Q′)∗μℛ(u,v)=μℛ(vi,vj). Then μℛ′(vi,vj)=μℛ(vi,vj).

Proof.

Since, ℋ is an IVFSG then it is obvious that, μℛ′−(vi,vj)≤μℛ−(vi,vj) and μℛ′+(vi,vj)≤μℛ+(vi,vj). We show that, μℛ′−(vi,vj)≮μℛ−(vi,vj) and μℛ′+(vi,vj)≮μℛ+(vi,vj). If possible let, μℛ′−(vi,vj)<μℛ−(vi,vj), then μℛ′−(vi,vj)=μQ′−(vi)∧μQ′−(vj)<μℛ−(vi,vj). Therefore, ⋀u∈(Q′)∗μQ′−(u)≤μQ′−(vi)∧μQ′−(vj)<μℛ(vi,vj)=⋀u,v∈(Q′)∗μℛ−(u,v), which contradicts Theorem 6. Therefore, μℛ′−(vi,vj)=μℛ−(vi,vj) and similarly it can be shown that μℛ′+(vi,vj)=μℛ+(vi,vj). Hence μℛ′(vi,vj)=μℛ(vi,vj).

Theorem 7.

Let Q′ be a maximal complete IVFQ in Z=(U,Q,ℛ). Then there is at least one u∈(Q′)∗ such that μQ′(u)=μQ(u).

Proof.

Let Q′ be a maximal complete IVFQ in Z=(U,Q,ℛ). Obviously, μQ′−(u)≤μQ−(u) and μQ′+(u)≤μQ+(u) for all u∈(Q′)∗. It is to prove that, ∃u∈(Q′)∗ such that μQ′−(u)=μQ−(u) and μQ′+(u)=μQ+(u). If possible let, μQ′−(u)<μQ−(u) for all u∈(Q′)∗. Define two crisp sets U1 and U2 be such that U1={u∈(Q′)∗:μQ′−(u)≤⋀v∈(Q′)∗μℛ−(u,v)} and U2={u∈(Q′)∗:μQ′−(u)>⋀v∈(Q′)∗μℛ−(u,v)}. Then (Q′)∗=U1∪U2. Then consider the following two cases:

Case-I. In this case, let us consider, U1=(Q′)∗ and take an arbitrary element u0∈U1 and construct an IVFS Q″ such that μQ″−(u)=μQ′−(u) and μQ″+(u)=μQ′+(u), whenever u≠u0 and for u=u0, μQ″−(u0)=μQ−(u0) and μQ″+(u0)=μQ+(u0), then Q′⊂Q″. Now,

μQ′′−(u)∧μQ′′−(u0)=μQ′−(u)∧μQ′′−(u0)≤⋀v∈(Q′)∗μℛ−(u,v)∧μQ−(u0) ≤μℛ(u,u0)∧μQ−(u0) ≤μℛ−(u,u0)for any u∈U1−{u0}.

and μQ″−(u)∧μQ′−(v)=μQ″−(u)∧μQ′−(v)≤μℛ−(u,v) for any u,v∈U1−{u0}. Therefore, by Theorem 3, Q″ is a complete IVFQ and which contradicts the maximality of Q′ since, Q′⊂Q″.

Case-II. Let us consider U1≠(Q′)∗, i.e., U2≠ϕ. Then take an arbitrary u0 of U2 be such that μQ′−(u0)=max{μQ′−(u):u∈U2} and define an IVFS Q″ by

μQ′′−(u)={μQ′−(u),u≠u0μQ−(u),u=u0μQ′′+(u)={μQ′+(u),u≠u0μQ+(u),u=u0

Then Q′⊂Q″. Now,

μQ′′−(u)∧μQ′′−(u0)=μQ′−(u)∧μQ−(u0)≤⋀v∈(Q′)∗μℛ−(u,v)∧μQ−(u0) ≤μℛ−(u,u0)∧μQ−(u0) ≤μℛ−(u,u0) for any u∈U1.

and μQ″−(u)∧μQ′−(u0)=μQ′−(u)∧μQ−(u0)≤μQ′−(u)∧μQ′−(u0)≤μℛ−(u,u0) when u∈U2 and μQ″−(u)∧μQ″−(v)=μQ′−(u)∧μQ′−(v)≤μℛ−(u,v) for any u,v∈(Q′)∗−{u0}. Therefore, by Theorem 3, Q″ is a complete IVFQ and which contradicts the maximality of Q′ since, Q′⊂Q″.

Therefore, considering the Cases I and II, it can be concluded that there is at least one u∈(Q′)∗ such that μQ′−(u)=μQ−(u). Making similar arguments, it can be also shown that there is at least one u∈(Q′)∗ such that μQ′+(u)=μQ+(u). Hence, for at least one u∈(Q′)∗, μQ′(u)=μQ(u).