Optimal Walking Gait Generator for Biped Robot Using Modified Jaya Optimization Technique
- DOI
- 10.2991/ijcis.d.200323.001How to use a DOI?
- Keywords
- Uncertain nonlinear biped robot system; Genetic Algorithm (GA); Particle Swarm Optimization (PSO); Jaya optimization algorithm; Central Force Optimization (CFO) algorithm; Modified Differential Evolution (MDE) algorithm; Gait optimization for biped robot; Zero moment point (ZMP) concept
- Abstract
This paper treats the optimization of the biped walking trajectory that can be used as a reference trajectory for control. The biped robot is modeled as a kinetic chain of 11 links connected by 10 joints. The inverse kinematics of the biped is derived for the specified positions of the hips and feet. The objective is to optimize the biped robot able to stably and naturally walking with preset foot-lift magnitude (or preset hip-shift, or preset step-length). The stability of the biped robot is quantified by the distance between the ZMP and the foot center in the step cycle, which represents the first objective function. Additionally, for the biped robot to follow the preset foot-lift value, the difference between the magnitude of foot-lift value and the foot-lift preset value represents the second objective function. Specifically, we minimize the value of the two objective functions by considering the gait parameters of biped robot as variables. The new Jaya optimization algorithm is innovatively applied to optimize the biped gait parameters as to ensure the biped robot walking robustly and steadily. The efficiency of the proposed Jaya-based identification method is compared with the Genetic Algorithm (GA), the Particle Swarm Optimization (PSO), the Central Force Optimization (CFO) and improved Differential Evolution (DE) [Modified Differential Evolution (MDE)] algorithms. The simulation results tested on the real small-sized biped robot system HUBOT-4 demonstrate that the novel proposed algorithm offers an efficient and stable gait for biped robot with precise foot-lift value.
- Copyright
- © 2020 The Authors. Published by Atlantis Press SARL.
- Open Access
- This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).
1. INTRODUCTION
The advanced biped robot walking mechanism is increasingly researched and developed in various aspects. Novel standards have been verified and applied to humanoid robots as to ensure more stable and natural gait gesture. Static stable walking is the first applied principle, in which the vertical projection of center of mass (CoM) on the ground is always to be kept within the supporting foot surface. In other words, humanoid robots can stop and move at any times during walking without falling apart. Based on its very simple manner, this principle is only successfully applied to slow-speed biped robots in which dynamic effects can be ignored [1,2]. Researchers then began to focus on developing dynamic walking [3]. This method allows the humanoid robot to speed up the pace. However, during locomotion process, the biped may fall due to environmental interference and cannot stop abruptly. Therefore, Zero Moment Point (ZMP)-based biped walking was proposed to help control and to handle biped inertia [4,5].
Numerous interesting researches have focused on improving the performance of humanoid robot walking gesture. Huang in [6] proposed a stable gait generator based on a newly proposed gait pattern in using the interpolation function. The method developed by D. Huan, through the Genetic Algorithm (GA), optimized the gait generator parameters as to help robot move steadily with the least amount of energy [7]. Dip et al. [8] exhibited steady gait for biped at constant velocity using the sine wave generator. Maximo et al. [9] introduced a new stable and quick model-free gait with specific arms movement for biped robots. Khusainov et al. [10] successfully combined kinematics and dynamics approaches in gait optimization for humanoid robot locomotion. The fact is that, nowadays, intelligent algorithms are being increasingly applied in this domain to optimize the gait generator parameters for humanoid robots such as GA [8], Particle Swarm Optimization (PSO) algorithm [11], Modified Differential Evolution (MDE) algorithm [12], Central Force Optimization (CFO) algorithm [13]. Shaffi in [14] introduced the humanoid robot achieved a stable gait by using the Fourier series-based gait generator. Furthermore novel approaches continually applied different intelligent algorithms to develop human robot stable and nature walking movement, such as bee swarm algorithm [15], T-S fuzzy controller [16], evolution techniques [17], recurrent neural networks optimized by Ant-Colony Optimization (ACO) [18] and so on. These intelligent algorithms have shown their effectiveness in gait generator for humanoid robot. However, there are still numerous areas for further improvement, especially those related to the computational cost of meta-heuristic algorithms.
Recently among newly proposed meta-heuristic optimization approaches, the powerful potential of the Jaya optimization algorithm has not yet being applied to optimize the biped robot walking gait generator. An enhanced optimization method, namely Jaya, initiatively introduced by Rao [19], proves compact and efficient to use with great benefit related to no need any particular control coefficients. Thus, it has been quickly used and improved for optimally solving different problems in various sectors such as mechatronics (Kumar et al. [20]; Rao et al. [21]), neural model identification (Suraj and Ghosh [22]), electronics (Bhoye et al. [23]), optimal civil problems (Venkata Rao and Saroj [24]; Du et al. [25]; Cong et al. [26]), control system implementation (Rao and More [27]; Rao and Saroj [28]) among others.
Enhancing with promising applications of the Jaya optimization algorithm, this paper intends to improve the modified Jaya approach for proposing a new approach of optimal nature-walking gait applied to biped robot.
In this paper, a new nature-walking pattern generation (n-WPG) is proposed which consists of gait generator for the two-foot trajectory, hip trajectory and the inverse kinematics in the full walking periodic sequence which can be seen as combination of three sub-sequences: Starting step, Periodic steps and Ending step. A combined objective function is newly introduced by linking two separate objective functions for humanoid robots that allows stable stepping with preset foot-lifting magnitude. The first one is based on ZMP criterion to stable stepping and the second is based on the difference between the magnitude of the foot-lift parameter and the foot-lift preset value. The Jaya algorithm is used to optimally identify the gait parameters for the biped as to reach steady nature-walking gait with accurate preset foot-lifting magnitude. The simulation and experiment results of proposed algorithm applied on the small-sized biped robot demonstrate the performance of the novel algorithm allowing the biped robot to move steadily and stably with an effectively reduced training time. The optimal nature-walking gait results attained by the proposed algorithm are comparatively tested with those obtained by well-known optimization approaches such as Modified Differential Evolution (MDE), CFO, GA and PSO algorithms.
The rest of this paper is arranged as follows: Section 2 fully presents the model design and implementation of the biped robot. In Section 3, inverse kinematics applied in biped optimized WPG parameters is presented. Section 4 presents the optimization results of the biped robot gait trajectory using Jaya technique in comparison with other four EAs algorithms. Section 5 presents the three Case Studies results. Finally, concluding remarks are given in Section 6.
2. BIPED MODEL IMPLEMENTATION
The analysis described in this research is based on a biped robot model shown in Figure 1. The origin of the fixed base reference coordinate B is located under Leg 1 on the ground plane. The x-axis points forward, the z-axis points upward and the y-axis is the cross product of z and x axes. The biped robot can be modeled as a kinetic chain of (2n + l) links connected by 2n revolute joints, where n = 5 is the number of degrees of freedom of each leg. Figure 1 shows the link and joint coordinate assignments and the values of physical parameters of the biped robot model are shown in Table 1.
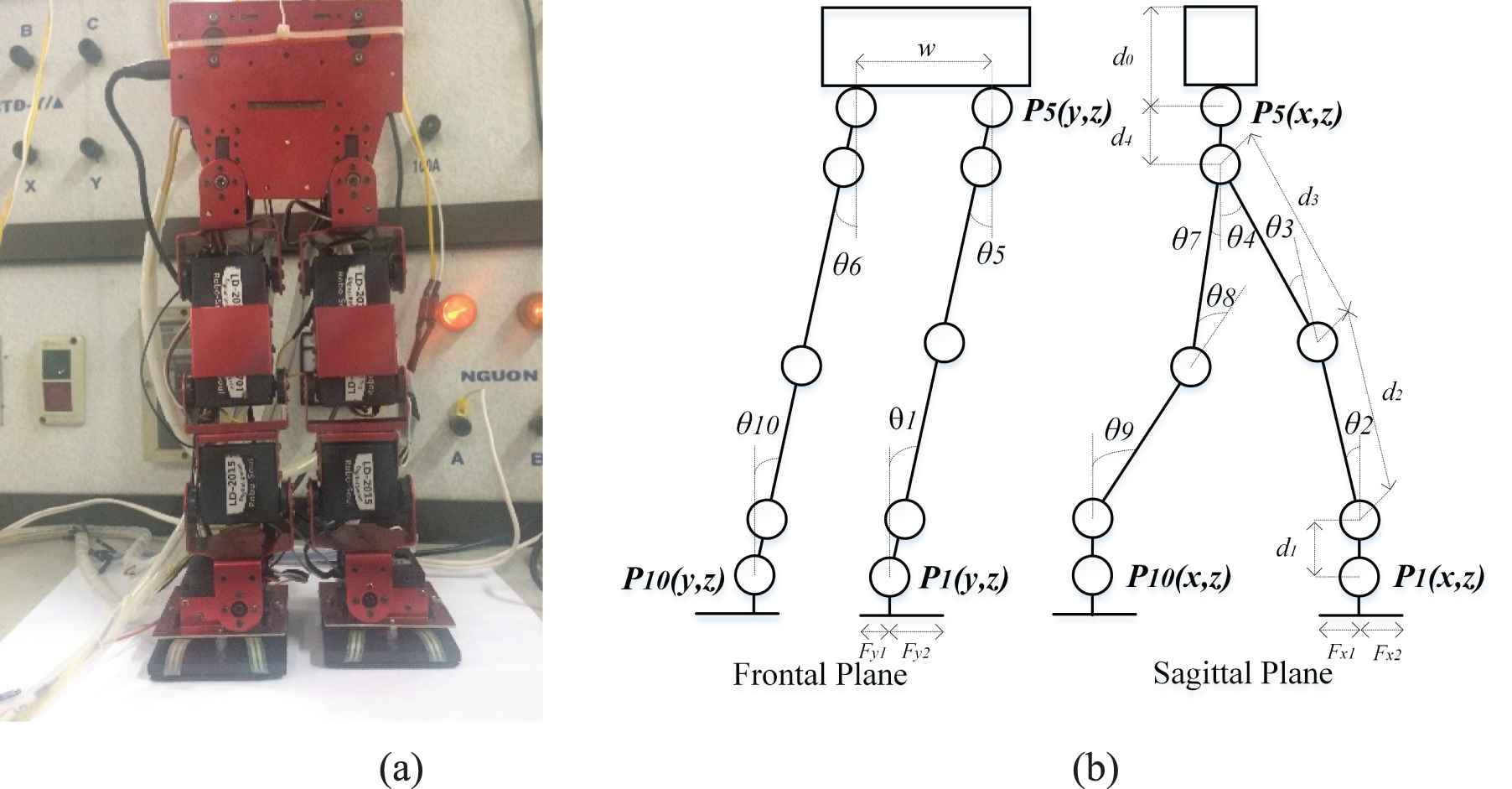
Biped robot model and coordinate configuration.
| Parameters | Value |
|---|---|
| 6.0 cm | |
| 4.5 cm | |
| 6.0 cm | |
| 6.0 cm | |
| 4.5 cm | |
| 6.6 cm | |
| 2.0 cm | |
| 4.0 cm | |
| 2.4 cm | |
| 70 g |
Physical parameters of biped robot (HUBOT-4).
The joint angle i is the rotation of frame i relative to frame (i−1) about axis zi. Each link has its mass mi concentrated at its CoM Pi = (Pix, Pyi, Pzi). The position of each link is computed from the 10 angles of rotation at one time in one step with the original coordination at the center of the supporting foot by direct kinematics, as Equations (1–3).
The balancing of the biped system can be simplified at an assigned ground point, called the ZMP (xZMP, yZMP, zZMP = 0), where the resultant moment at the ground plane is zero. The location of the ZMP [5] is
Constraints on the motion of the biped robot are that the location of the ZMP must be inside the convex hull of the support foot or feet. We assume the frictional coefficient is large enough so that the frictional constraint is negligible.
3. INVERSE KINEMATICS
To describe the specific configuration of the biped robot, we assign the motions of link 1 (foot 1), link 6 (body) and link 11 (foot 2). By fixing both the position and the orientation of these three links, the configuration of the biped robot is established. For simplicity, we assume that no rotational motion occurs for these three links during walking. In order to compute the joint motion, the inverse kinematic model is needed for given P1 = (P1x, P1y, P1z), P5 = (P5x, P5y, P5z) and P10 = (P10x, P10y, P10z) where Pi is the reference point of link i as shown in Figure 1. Because there is no rotation, the joint angles can be expressed by,
The coordination
In that, d0 represents the length of the upper body, d1 is the distance between two points P1 and P2, d2 is the distance between two points P2 and P3, d3 is the distance between two points P3 and P4, d4 represents the distance between two points P4 and P5, w represents the distance between 2 legs. Therefore, the biped motion can be expressed solely by positions P1, P5 and P10. A flowchart for computing the ZMP from the trajectories of P1, P5 and P10 is shown in Figure 2.

Calculation of the zero moment point.
4. OPTIMIZATION OF THE BIPED ROBOT TRAJECTORY
The trajectory optimization is based on an objective functional, involving the biped robot able to stably and naturally walking with preset foot-lift magnitude, with the gait parameters of biped robot as variables. Specifically, we define the optimization problem as follows:
The goal of biped robot is to achieve a stable gait with preset foot-lift value. For this purpose, the ZMP point is to always be ensured within the foot area [6]. If the ZMP is within the area of the supporting leg, the robot does not fall [7]. The calculation of the ZMP of biped robots in walking is shown in Figure 2. The stability of the humanoid robot is quantified by the distance between the ZMP and the foot center in the step cycle. Walking gait with maximum stability is obtained by minimizing the function f1 in Equation (8) [1]:
Additionally, for the humanoid robot to follow the preset foot-lifting height value –
Thus, in order for biped robot to obtain a steady gait with the foot-lift set up in advance, we find the minimum value of the two objective functions
To solve the problem, algorithm diagram of optimal walking gait for biped robots is shown in Figure 3. The n-WPG composes of the gait generator of the two-foot trajectory, the hip trajectory and the biped inverse kinematics (see additional works at [4]). The meta-heuristic optimization algorithms are used to create 4 gait parameters (S, H, h, n) that provide the n-WPG in which outputs of the n-WPG are to create 10 angles for biped robot. The output of biped robot is the location of ZMP points as described in Figure 2. The optimal target function identified by the meta-heuristic optimization algorithm is a biped robot that walks steadily with the desired foot-lift, as presented in Equation (9). The following difference approximation is used to calculate the derivatives:
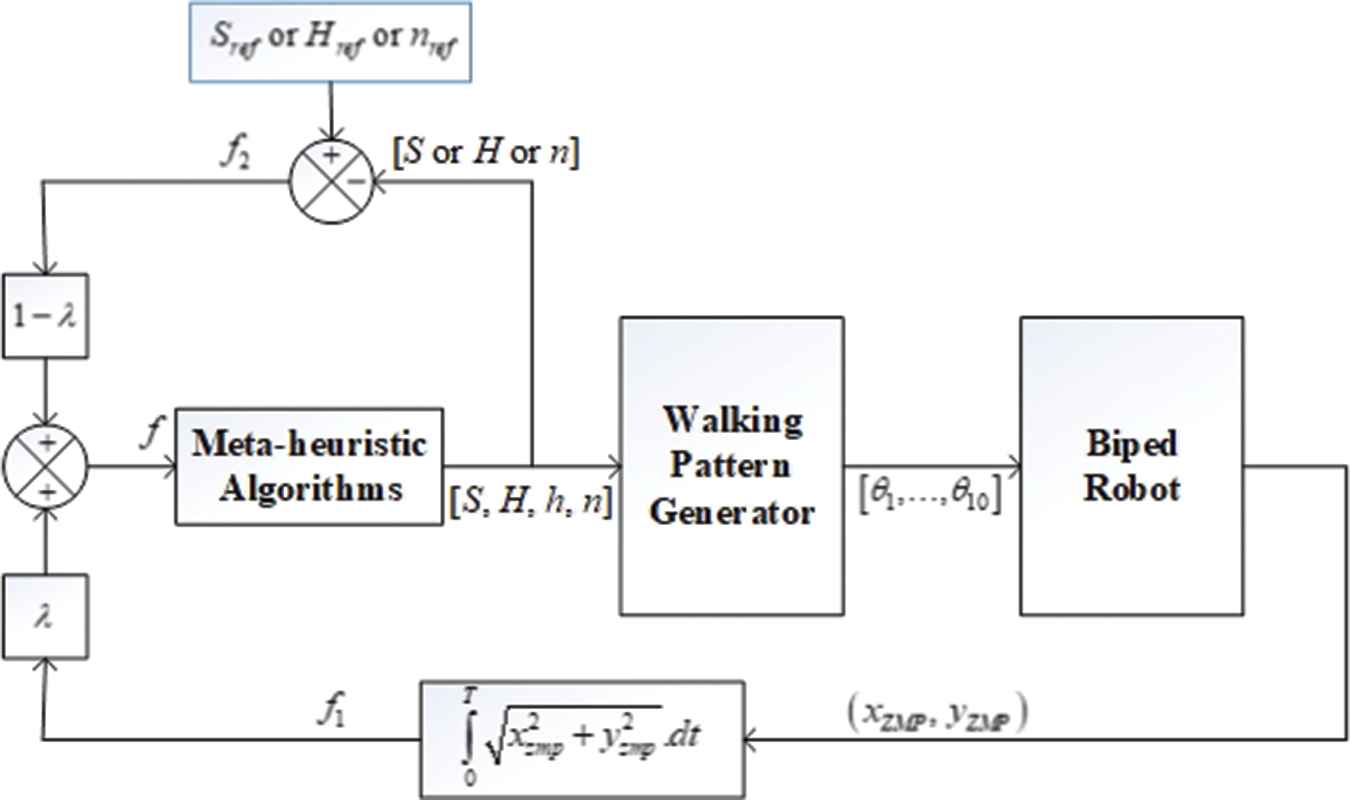
Algorithm diagram of optimal walking gait for biped robot.
In the simulation, (
The biped robot HUBOT-4 will walk stably with the preset foot-lift value. The coefficient
| Parameters | Lower Bound (cm) | Upper Bound (cm) |
|---|---|---|
| S-Step length | 8 | 12 |
| H-foot lifting | 0.1 | 5 |
| h-kneeling | 1.1 | 1.5 |
| n-hip swinging | 0.1 | 6 |
Bounds for four key walking gait parameters of humanoid HUBOT-4.
Simulation results are carried with MATLAB platform run with 2.49 GHz CPU & 8 GB RAM. Every method is tested 30 times. Table 3 eventually presents the GA, PSO, CFO, MDE and Jaya optimally selected parametric values.
| Method | Parameters | Value |
|---|---|---|
| GA | Mutating rate | 0.2 |
| Crossover rate | 0.7 | |
| PSO | Accelerated factor 1 | 2 |
| Accelerated factor 1 | 2 | |
| Inertia factor | 0.4 | |
| CFO | Alpha | 0.25 |
| Beta | 0.35 | |
| Gamma | 0.95 | |
| Frep | 0.5 | |
| deltaFrep | 0.05 | |
| MDE | Mutation value (F) | Random [0.4; 1.0] |
| Crossover probability (CR) | Random [0.7; 1.0] | |
| Jaya | No parameters | No |
GA, Genetic Algorithm; PSO, Particle Swarm Optimization; CFO, Central Force Optimization; MDE, Modified Differential Evolution.
Parameters of CFO, MDE and Jaya algorithm.
Specify the foot-lifting height of biped HUBOT-4 being
| No | Optimal Objective Function |
Run (Second) | |||
|---|---|---|---|---|---|
| Best | Worst | Mean | Variance | ||
| Jaya | 101.856724029548 | 1.01856724e+02 | 1.018567240000001e+02 | 3.3425940701226e-27 | 157 |
| MDE | 101.856724029550 | 1.01856724e+02 | 1.018567260000000e+02 | 3.5178160847427e-13 | 153 |
| CFO | 101.889479300000 | 1.027262942e+02 | 1.026317738400000e+02 | 0.606345370124322 | 159 |
| PSO | 101.856724029549 | 1.027262942e+02 | 1.018857096733334e+02 | 0.025205077757601 | 152 |
| GA | 101.927584300000 | 1.030504002e+02 | 1.022916734133333e+02 | 0.057276108848447 | 158 |
GA, Genetic Algorithm; PSO, Particle Swarm Optimization; CFO, Central Force Optimization; MDE, Modified Differential Evolution.
Performance comparisons in optimal fitness function.
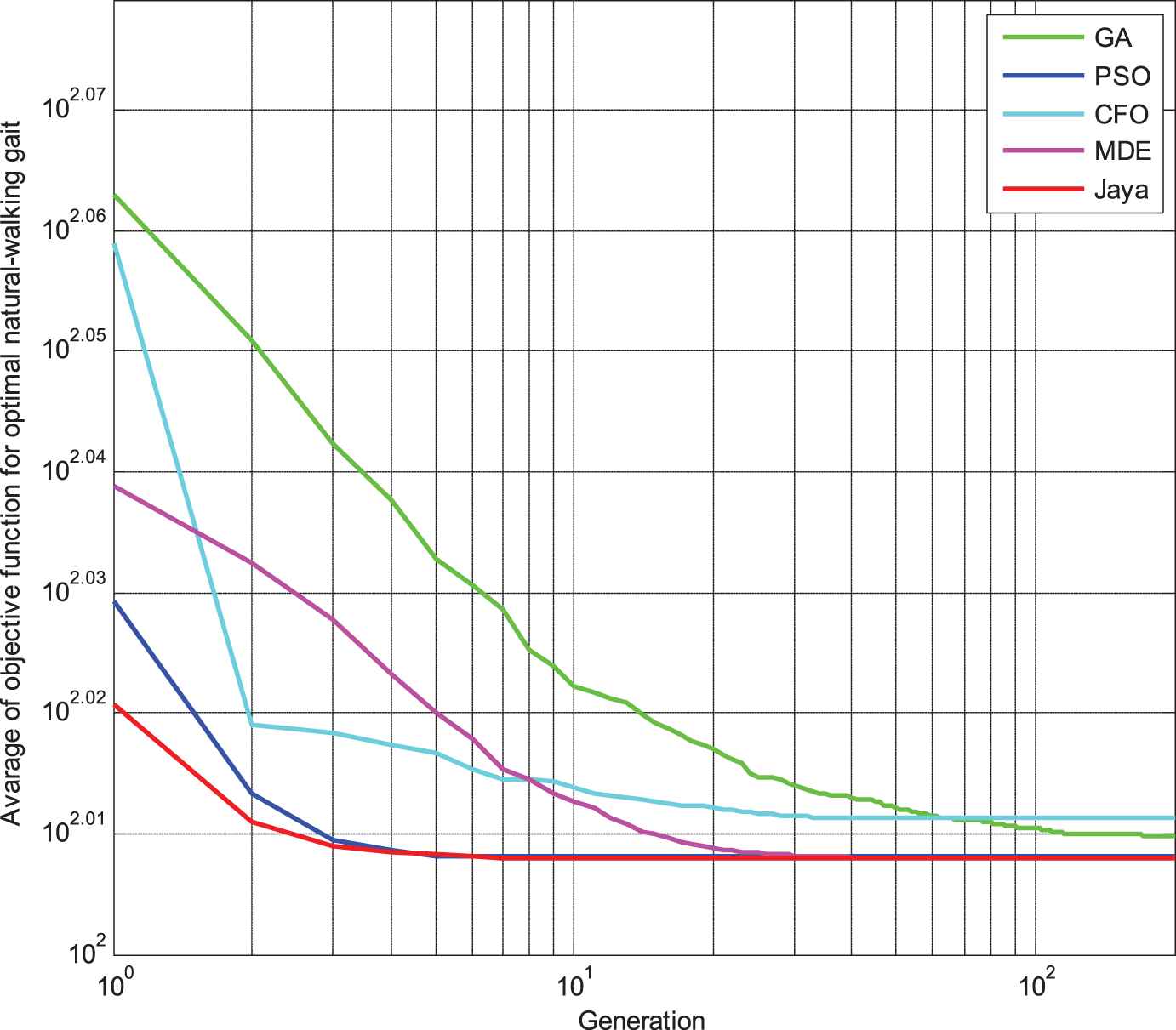
Convergence rate of the comparative algorithms in the optimal process.
The optimum set of 4 key parameters for biped HUBOT-4 conformed to the objective derived from 30 runs per GA, PSO, CFO, MDE and proposed Jaya algorithms is shown in Table 5.
| Href = 2 cm |
|||||
|---|---|---|---|---|---|
| Algorithms | Walking Gait Parameters Value |
Best Fitness Value f (cm) | |||
| S (cm) | H (cm) | h (cm) | n (cm) | ||
| GA | 11.99 | 1.99 | 1.1 | 5.97 | 101.927584300000 |
| PSO | 12.00 | 1.99 | 1.1 | 6.00 | 101.856724029549 |
| CFO | 11.97 | 1.99 | 1.1 | 5.97 | 101.889479300000 |
| MDE | 12.00 | 2.00 | 1.1 | 5.99 | 101.856724029550 |
| Jaya | 12.00 | 2.00 | 1.1 | 6.00 | 101.856724029548 |
GA, Genetic Algorithm; PSO, Particle Swarm Optimization; CFO, Central Force Optimization; MDE, Modified Differential Evolution.
Resulted parametric set for five comparative algorithms.
Based on the results described in Figure 4, it is important to notice that the Jaya algorithm searches for an optimal solution with an average value of 101.856724000000 after about 55 generations, while the MDE algorithm is approximately 134 generations after the search, finding an optimal solution obtained an average value of 101.856724300000, while the CFO algorithm must need around 158 generations to find the optimal solution with an average value of 102.626134800000, while the PSO algorithm is approximately 41 generations after the search, finding an optimal solution obtained an average value of 101.885709700000, while the GA algorithm must need around 190 generations to find the optimal solution with an average value of 102.291673400000. These results demonstrate that the Jaya algorithm outperforms GA, PSO, CFO and MDE in terms of convergence speed with the best target function value.
Table 5 shows the comparative optimized results of GA, PSO, CFO, MDE and proposed Jaya. The difference between the magnitude of the foot-lift value -
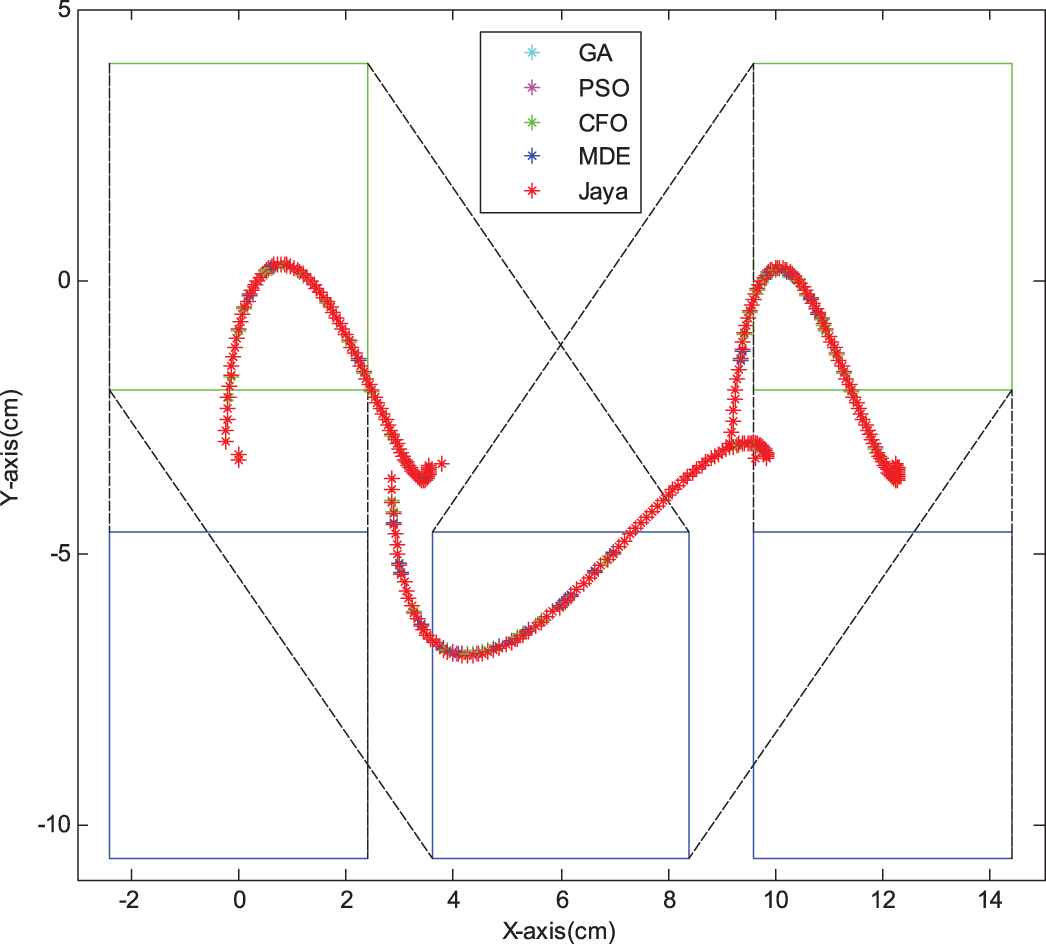
Resulted comparative Zero Moment Point (ZMP) survey.
The comparatively resulted ZMP trajectories using the five techniques illustrated in Figure 5 show that they surely keep in the supporting foot surface and it proves that biped allowing steadily robust stepping.
5. CASE STUDIES
The optimum identified solutions based on four principal biped WPG coefficients using proposed Jaya technique illustrated in Tables 6–8 which will strongly demonstrate that the eventual purpose of this study is completed with respect to the three following case studies which are investigated regarding to the preset foot-lift, the preset hip-shift and the preset step-length magnitudes, respectively.
| Href (cm) | Jaya Optimization Results |
|||
|---|---|---|---|---|
| S (cm) | H (cm) | h (cm) | n (cm) | |
| 2.0 | 12.0000 | 2.0000 | 1.1000 | 6.0000 |
| 3.0 | 12.0000 | 3.0000 | 1.1000 | 6.0000 |
The bold values represent the reference values based on them to optimize the parameter set using Jaya.
Optimal parameter set.
| nref (cm) | Jaya Optimization Results |
|||
|---|---|---|---|---|
| S (cm) | H (cm) | h (cm) | n (cm) | |
| 4.0 | 12.0000 | 1.5000 | 1.1000 | 4.0000 |
| 5.0 | 12.0000 | 1.5000 | 1.1000 | 5.0000 |
The bold values represent the reference values based on them to optimize the parameter set using Jaya.
Optimal parameter set.
| Sref (cm) | Jaya Optimization Results |
|||
|---|---|---|---|---|
| S (cm) | H (cm) | h (cm) | n (cm) | |
| 9.0 | 9.0000 | 2.0000 | 1.1000 | 6.0000 |
| 10 | 10.0000 | 1.0000 | 1.1000 | 6.0000 |
The bold values represent the reference values based on them to optimize the parameter set using Jaya.
Optimal parameter set.
5.1. Case Study-1: Biped Optimal Stable Walking with Preset Foot-lift Href Magnitudes
Table 6 demonstrates the optimized value of the walking gait parameters to ensure the biped HUBOT-4 to walk steadily with both cases corresponding to different preset foot-lift magnitudes. (

Convergence rate of the proposed Jaya algorithm in the optimal process.
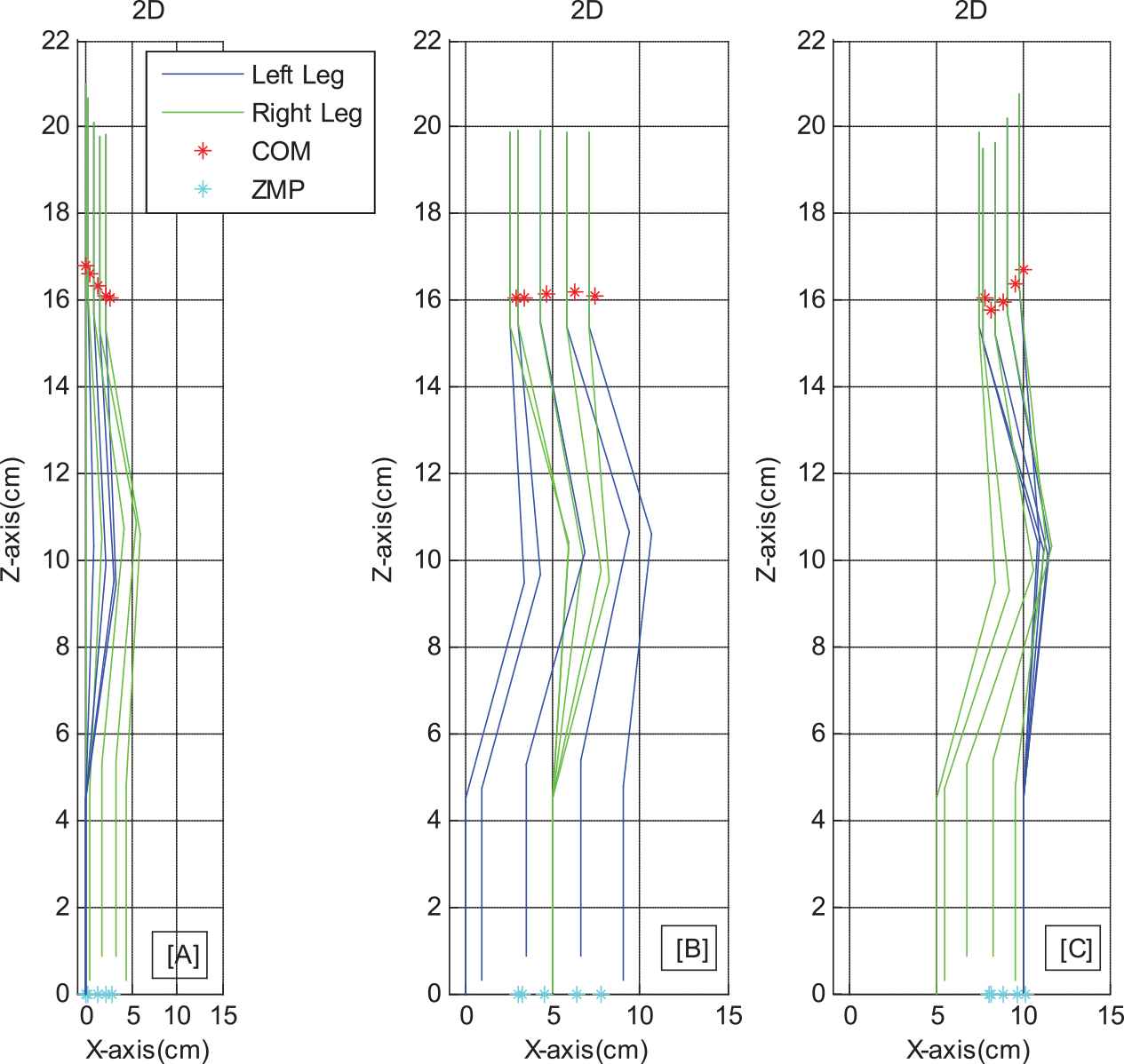
Continually Figure 7a and 7b illustrates the 2D gait in the X-Z plane of the HUBOT-5, corresponding to two cases with different preset foot-lift amplitudes. The results from Table 6 and Figure 7 show that the biped HUBOT-4 attains a pickup lift in term of the preset foot-lift value.
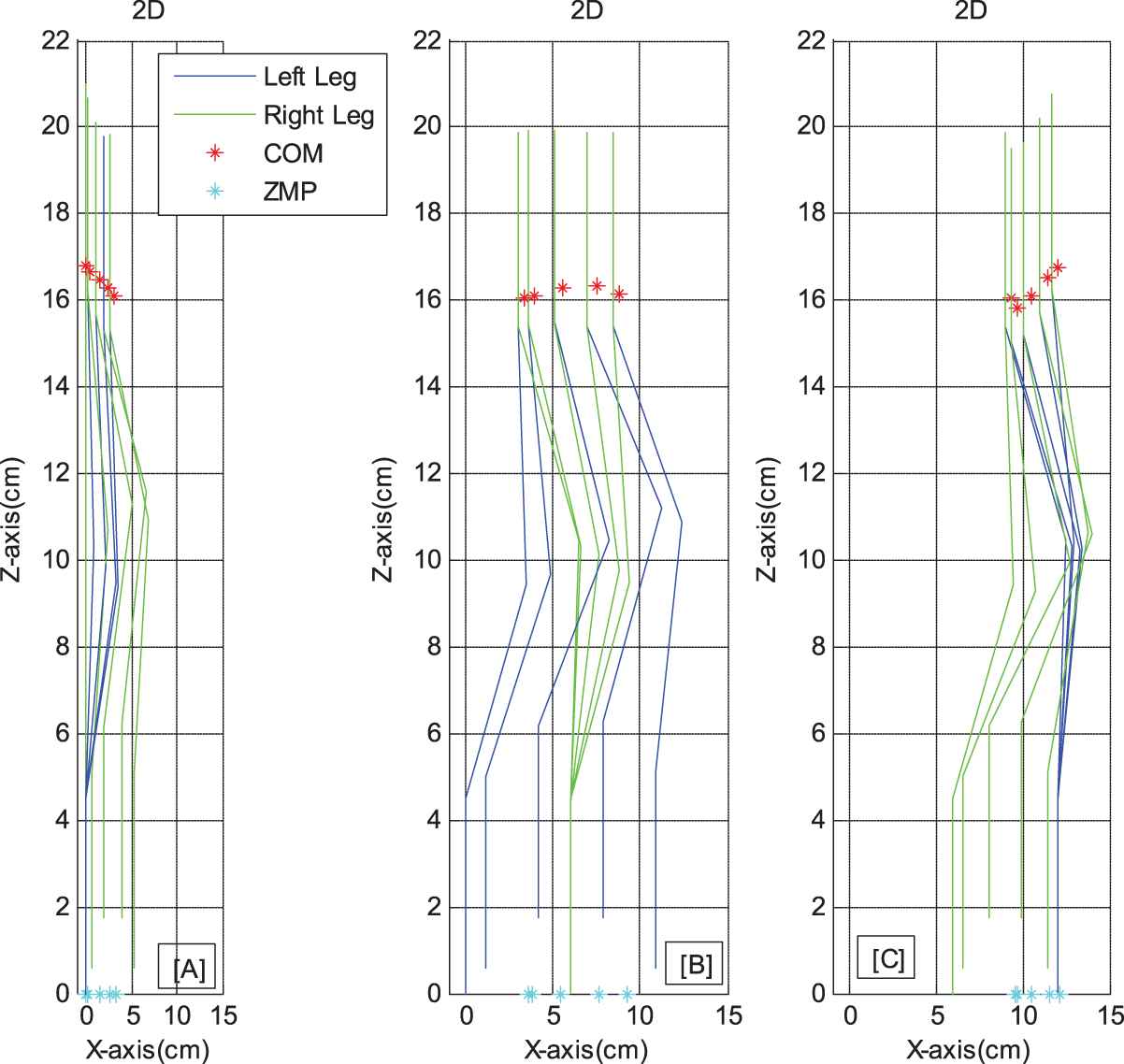
Stick diagram of biped robot for a nature-walking sequence in the x-z plan. [A]: Starting step. [B]: Periodic steps. [C]: Ending step.

Stick diagram of biped robot for a nature-walking sequence in the x-z plan. [A]: Starting step. [B]: Periodic steps. [C]: Ending step.
Furthermore Figure 8a and 8b illustrates the resulted ZMP point trajectory and the projection of GCOM trajectory for two different preset foot-lifting amplitudes. This result shows that the ZMP point is always in the supporting foot area and then it ensures that the HUBOT-4 biped robot surely keeps stable walking.

Resulted Zero Moment Point (ZMP) và Grounded-Center-Of-Mass (GCOM) trajectories.

Resulted Zero Moment Point (ZMP) và Grounded-Center-Of-Mass (GCOM) trajectories.
Figure 9 below demonstrates the 10 rotary angular trajectories in one stepping cycle of the two legs of biped HUBOT–4
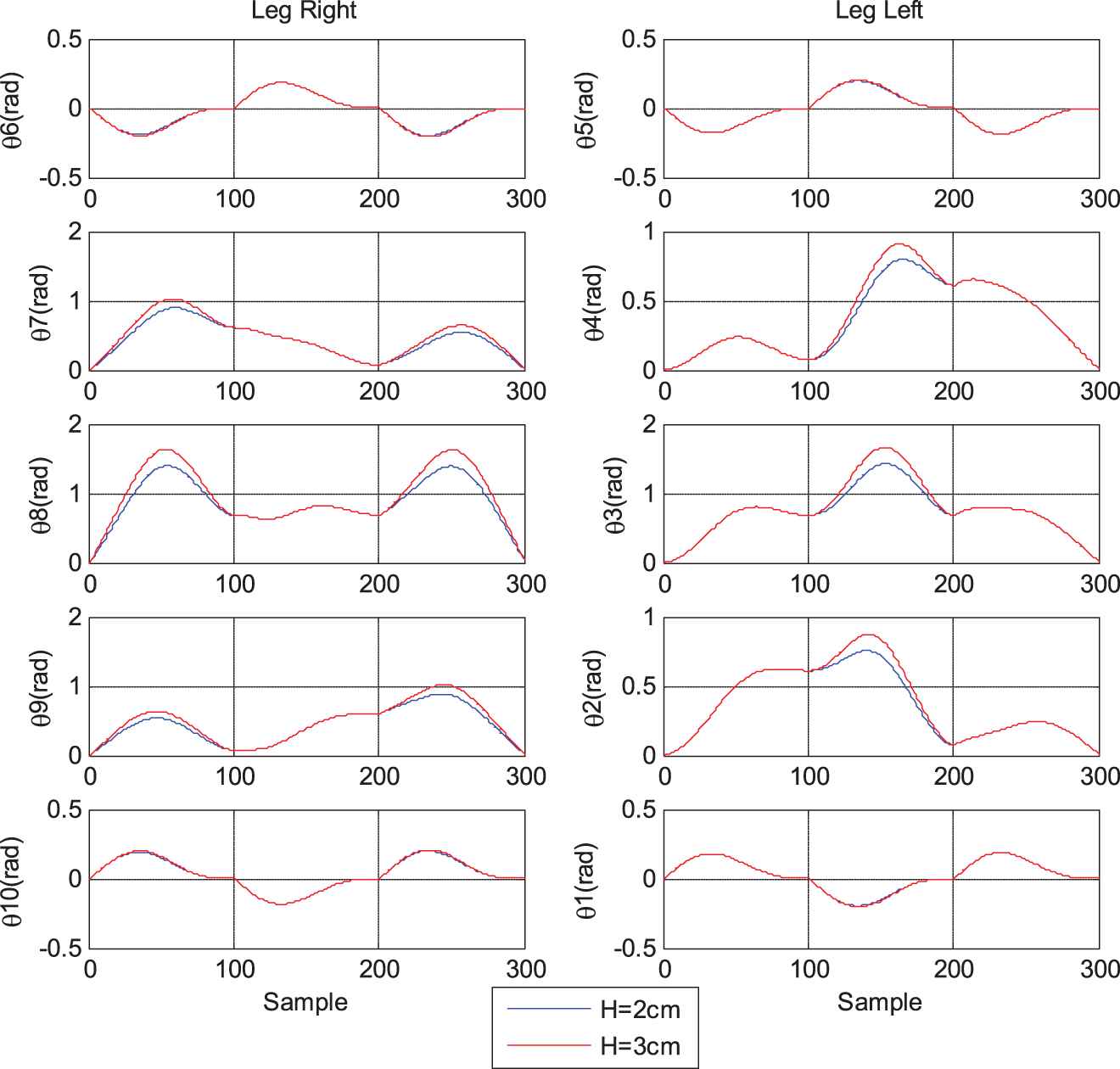
Trajectories of the ten joint angles located at two legs of biped HUBOT-4.
Based on the results of the optimization and simulation shown in Table 6, Figures 7–9, which convincingly demonstrate that the work of preset foot-lift parameter -
5.2. Case Study-2: Biped Optimal Stable Walking with Preset Hip-Shift nref Values
Table 7 demonstrates the optimum identified value of proposed WPG to guarantee the biped robot to step stably in two different cases regarding to various preset hip-shift values (
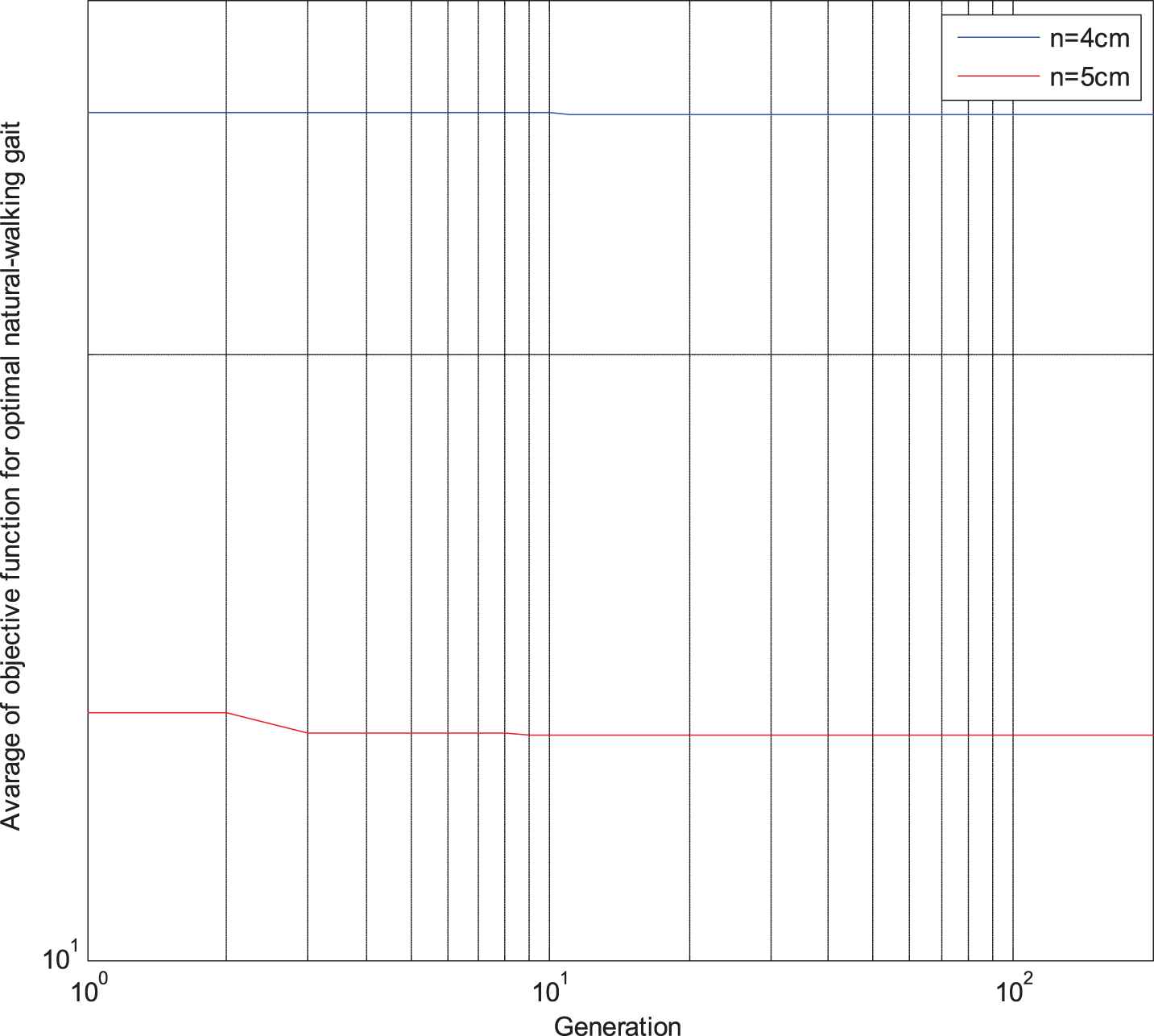
Convergence rate using the proposed Jaya algorithm in the optimal procedure.
Furthermore Figure 11a and 11b below presents the resulted 2D gait in the Y-Z co-ordinate of the biped, with respect to three different cases of preset hip-shift values. Results from Table 7 and Figure 11 strongly ensure that the humanoid robot successfully obtains a desired hip-shift value in control process.
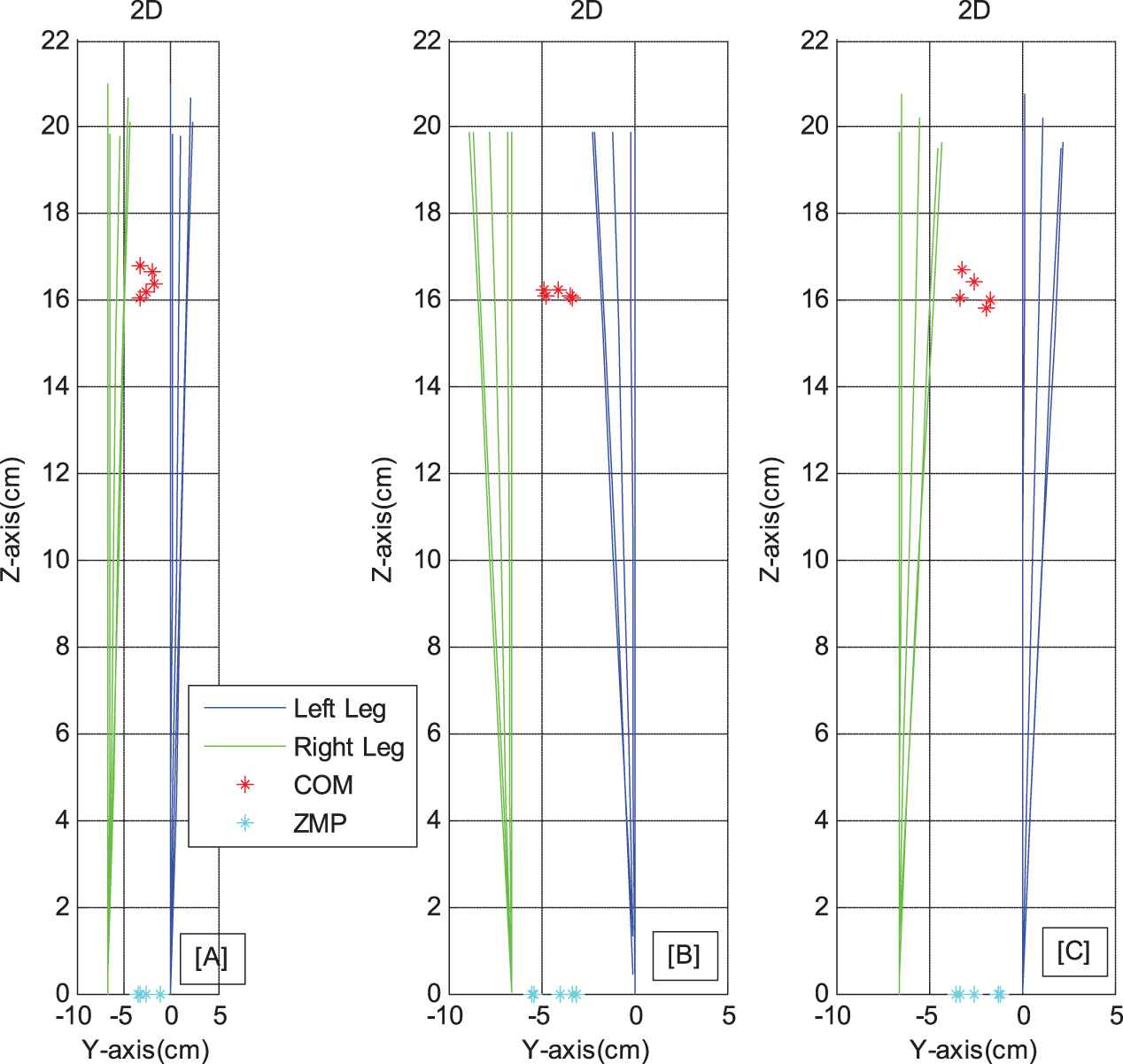
Resulted 2D gait of humanoid robot with

Resulted 2D gait of humanoid robot with
Figure 12 illustrates the resulted ZMP values for two preset hip-shift magnitudes. These results confirm that ZMP trajectory is always to be kept inside the supporting footprint surface and thus guarantees humanoid robot walking efficiently and robustly.
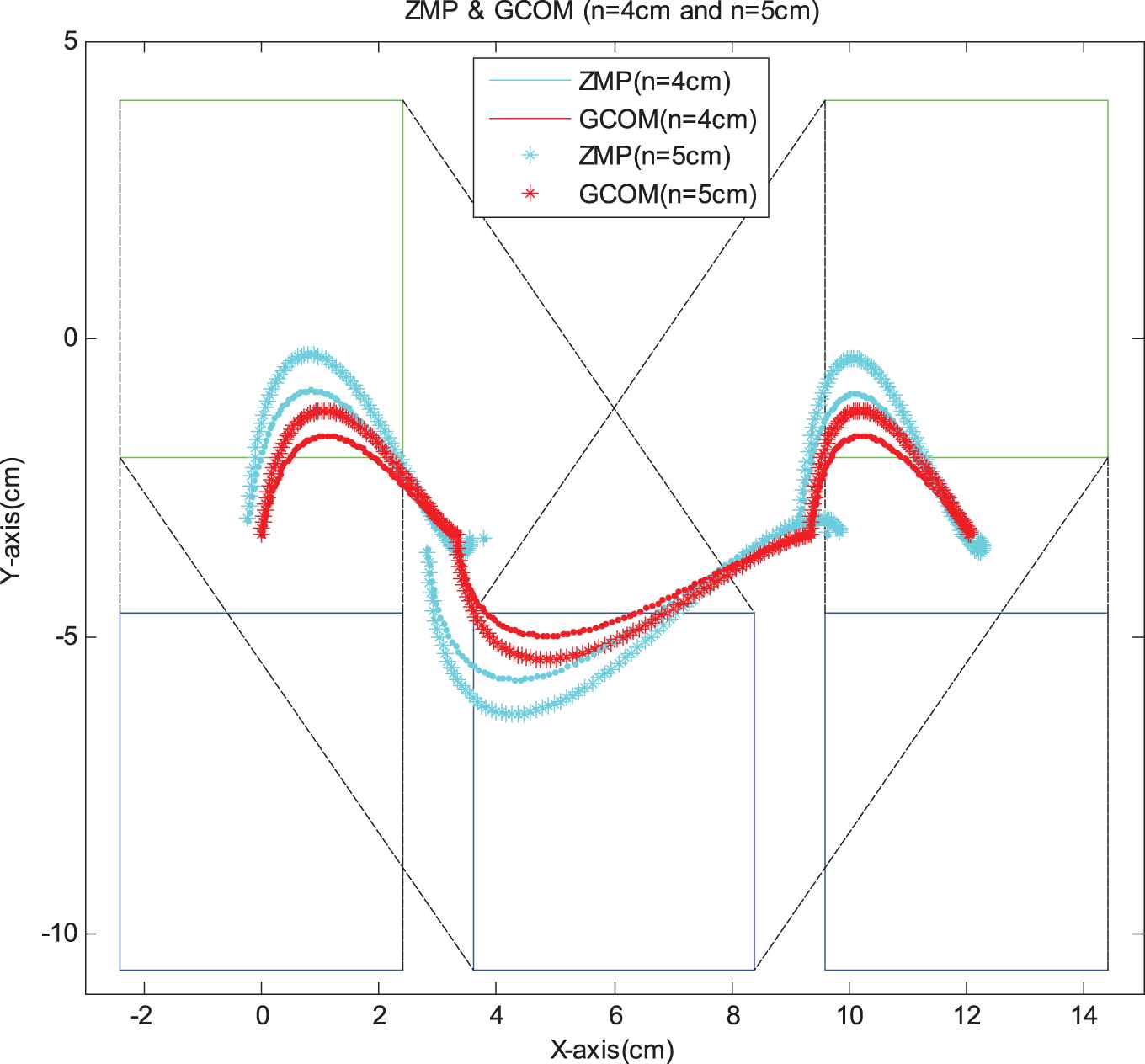
Resulted Zero Moment Point (ZMP) trajectories.
Figure 13 demonstrates the 10 rotary angular trajectories in one stepping cycle of the two legs of biped HUBOT–4
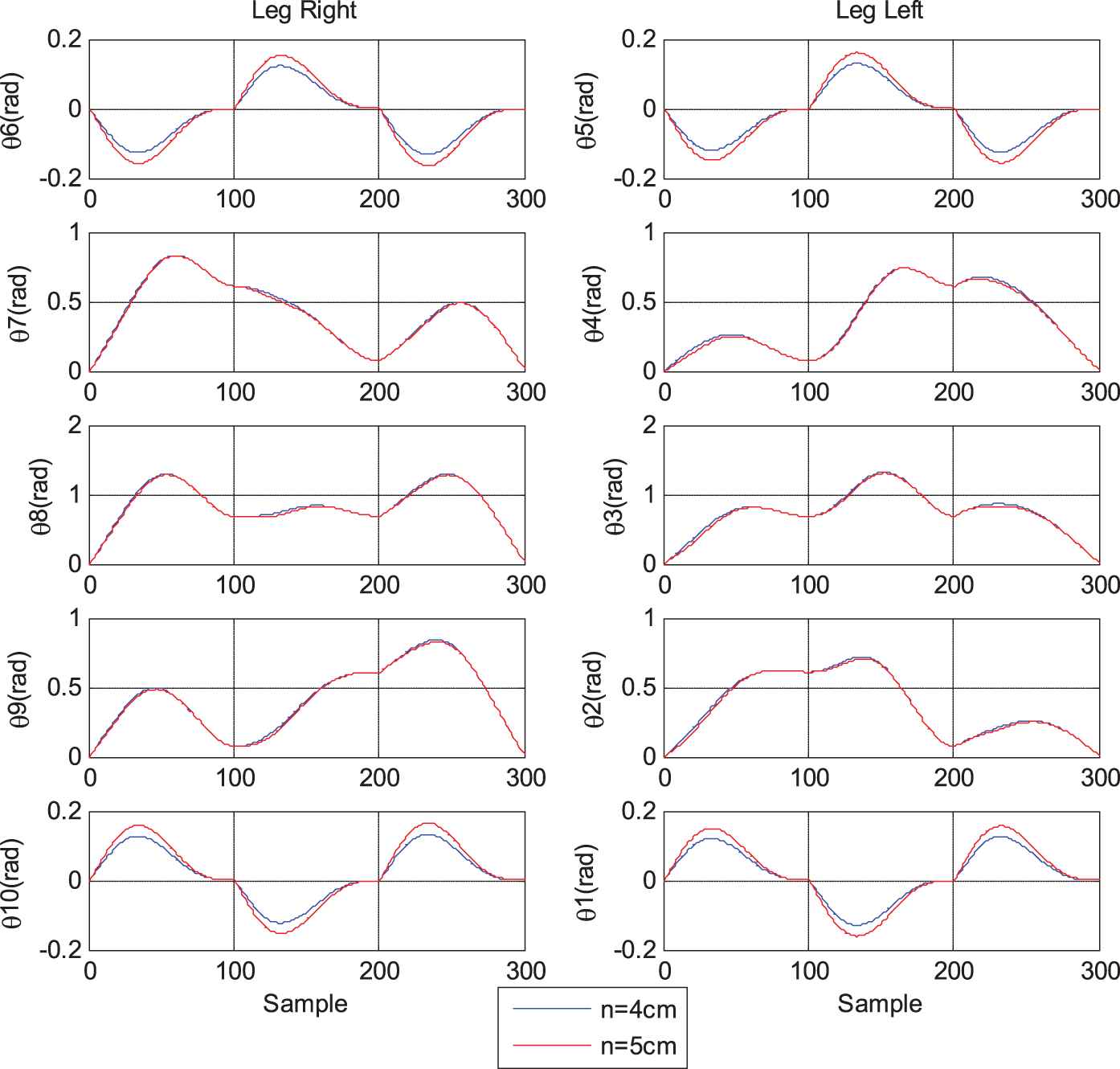
Trajectories of the ten joint angles located at two legs of biped HUBOT-4.
In summary based on the results of the optimization and simulation shown in Table 7, Figures 11–13, which once more demonstrate that the work of preset hip-shift parameter -
5.3. Case Study-3: Biped Optimal Stable Walking with Preset Step-Length Sref Values
Table 8 demonstrates the optimum identified value of proposed WPG to guarantee the humanoid robot to step stably in two different cases regarding to various preset step-length values (

Convergence rates optimized with proposed Jaya algorithm in the optimal procedure.
Continually Figure 15a and 15b presents the resulted 2D gait in the X-Z co-ordinate of the biped, with respect to different cases of preset step-length values. Results from Table 8 and Figure 15 strongly ensure that the biped robot successfully obtains a desired step-length value in control process.

Resulted 2D gait of biped robot with step-length
Resulted 2D gait of biped robot with
Then Figure 16a and 16b illustrates the resulted ZMP values for two preset step-length magnitudes. These results confirm that ZMP trajectory keeps inside the supporting footprint surface and thus guarantees humanoid robot walking efficiently and robustly.

Resulted Zero Moment Point (ZMP) trajectories with

Resulted Zero Moment Point (ZMP) trajectories with
Consequently results from Figure 17 demonstrate the 10 rotary angular trajectories in one stepping cycle of the two legs of biped HUBOT–4
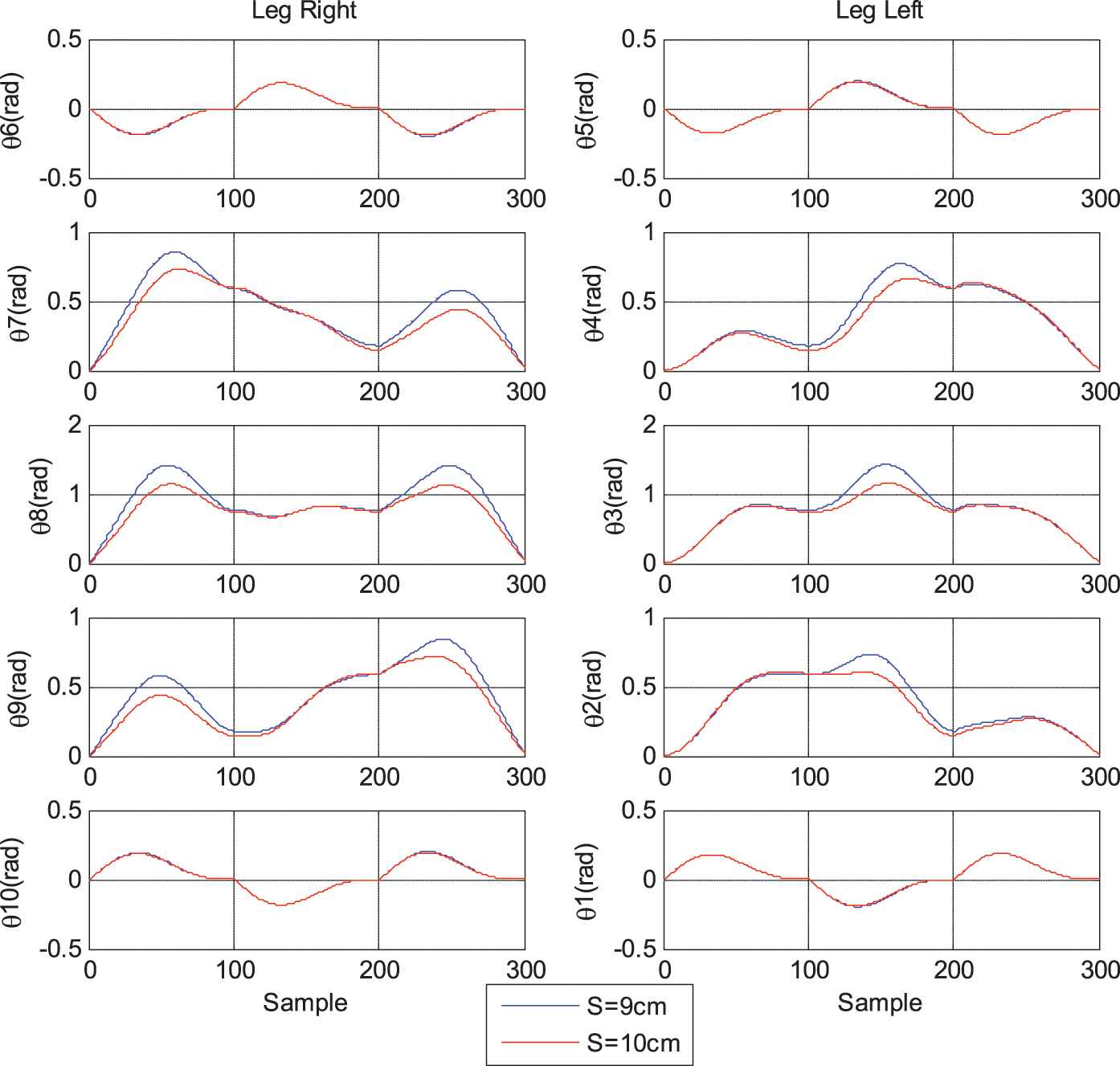
Trajectories of the ten joint angles located at two legs of biped HUBOT-4.
In summary based on the results of the optimization and simulation shown in Table 8, Figures 15–17, which once more strongly demonstrate that the work of preset step-length parameter -
6. CONCLUSIONS
In this paper the optimization of the biped walking gait trajectory available to stably and naturally walking with preset step-length magnitude, has been obtained by quantifying the distance between the ZMP and the foot center in the step cycle and optimally quantifying the difference between the magnitude of step-length value and the step-length preset one. We applied Jaya optimization algorithm to minimize them by treating the gait parameters of biped robot as variables. This innovative concept has been verified by a computer simulation of a real biped robot HUBOT-4. Since the optimization process is performed for each time interval, the proposed technique can generate the biped gait trajectory in real-time.
CONFLICTS OF INTEREST
Authors confirm that there is no any conflict of interest in this paper.
AUTHORS' CONTRIBUTIONS
Anh H.P.H.: conception, final rewriting, corresponding. Huan T.T.: software, draft writing, data collecting and checking.
ACKNOWLEDGMENTS
This research is fully funded by National Foundation for Science and Technology Development (NAFOSTED), Viet Nam under grant MDT 107.01-2018.10.
REFERENCES
Cite this article
TY - JOUR AU - Ho Pham Huy Anh AU - Tran Thien Huan PY - 2020 DA - 2020/04/03 TI - Optimal Walking Gait Generator for Biped Robot Using Modified Jaya Optimization Technique JO - International Journal of Computational Intelligence Systems SP - 382 EP - 399 VL - 13 IS - 1 SN - 1875-6883 UR - https://doi.org/10.2991/ijcis.d.200323.001 DO - 10.2991/ijcis.d.200323.001 ID - Anh2020 ER -
