International Journal of Computational Intelligence Systems

<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Volume 12, Issue 1, November 2018, Pages 250 - 258

A Hybrid Learnt Clause Evaluation Algorithm for SAT Problem

Authors
Guanfeng Wu1, 2, *, Qingshan Chen1, 2, Yang Xu2, Xingxing He2
1School of Information Science and Technology, Southwest Jiaotong University, Chengdu 610031, Sichuan, P.R. China
2National-Local Joint Engineering Laboratory of System Credibility Automatic Verification, Southwest Jiaotong University, Chengdu 610031, Sichuan, P.R. China
*

Corresponding author. Email: wl520gx@gmail.com

Received 20 October 2018, Revised 30 October 2018, Accepted 4 November 2018, Available Online 19 November 2018.
DOI
10.2991/ijcis.2018.125905645How to use a DOI?
Keywords
SAT problem; Parallel SAT solver; VSIDS; LBD; GLUCOSE
Abstract

It is of great theoretical and practical significance to develop the efficient SAT solvers due to its important applications in hardware and software verifications and so on, and learnt clauses play the crucial role in state of the art SAT solvers. In order to effectively manage learnt clauses, avoid the geometrical growth of learnt clauses, reduce the memory footprint of the redundant learnt clauses and improve the efficiency of the SAT solver eventually, learnt clauses need to be evaluated properly. The commonly used evaluation methods are based on the length of learnt clause, while short clauses are kept according to these methods. One of the current mainstream practices is the variable state independent decaying sum (VSIDS) evaluation method, the other is based on the evaluation of the literals blocks distance (LBD). There have been also some attempts to combine these two methods. The present work is focused on the hybrid evaluation algorithm by combining the trend intensity and the LBD. Based on the analysis of the frequency of learnt clauses, the trend of learnt clause being used is taken as an evaluation method which is then mixed with the LBD evaluation algorithm. The hybrid algorithm not only reflects the distribution of learnt clauses in conflict analysis, but also makes full use of literals information. The experimental comparison shows that the hybrid evaluation algorithm has advantages over the LBD evaluation algorithm in both the serial version and the parallel version of SAT solver, and the number of problems solved has significantly increased.

Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

1. INTRODUCTION

The SAT (Boolean satisfiability) problem is the basic problem of logic and computer science, and also is the first NP-complete problem that has been proven [1]. Many problems of natural science can be transformed into SAT problems [2–4], such as transportation, integrated circuit automatic routing, code automatic generation, software verify-cation, etc. It is of great theoretical and practical significance to develop the efficient SAT solvers. The algorithms of SAT solving can be divided into two types: complete algorithm and incomplete algorithm. A complete algorithm must be able to determine the satisfiability of the formula in theory. However, the incomplete algorithm is not guaranteed to find solutions to the problem. The solvers and algorithms involved in this paper refer to complete algorithms.

From the introduction of the Davis–Putnam–Logemann–Loveland (DPLL) algorithm in 1960 to the publication of conflict driven clause learning (CDCL) algorithm [5–7]. The SAT solvers have evolved over decades. Their modules tend to be stable. The state of art SAT solvers are both based on the framework of DPLL or CDCL algorithms [8–14], such as MiniSAT, Glucose, MapleCOMSPS, Kiel, etc. Including but not limited “simplification”, “two literals watched”, “decision variable selection”, “Boolean Constraint Propagation (BCP)”, “CDCL”, “branch backtracking”, “restart”, “clause management” modules.

A large number of learnt clauses will be generated by a CDCL-based SAT solver during the solution process. Take a benchmark “g2-ak128modbtbg2msisc.cnf” from Main Track in SAT Competition (2017) as an example. The total number of literals are 296 051 and the number of clauses are 968 713. There are 16 007 084 learnt clauses generated by Glucose, and 15 204 538 learnt clauses are deleted during search. The rate of the deletion is almost 95%. The memory resources are occupied by excessive learnt clauses, and this increases the time complexity of traversing clauses during search. So, learning too much clauses means that the solver has to sort the “good” clauses to be used.

GRASP [7] found the influence of learnt clauses on the search process in experiments. The learnt clauses increased exponentially and reduced the efficiency of searching. To avoid this, it deletes learnt clauses which length (the number of literals in the clause) greater than 30.

Chaff uses the number of unassigned variables as the condition for the clause to be deleted. When the number of unassigned variables in the learnt clause reaches the threshold, the learnt clause is deleted [8].

Minisat uses the variable state independent decaying sum (VSIDS) evaluation method. The activity is set for the clause, and the clauses are sorted according to the activity, and the half of the learnt clauses with low activity are periodically deleted [13].

Precosat is the champion solver for the SAT Competition (2009). It uses VSIDS to evaluate the learnt clauses and adds preprocessing techniques to the binary clauses, making full use of the role of the binary clauses in conflict analysis [15].

Glucose uses the value of literals blocks distance (LBD) as the basis of retaining the learnt clause [11].

In addition, Lingeling uses a hybrid evaluation method of VSIDS and LBD [16].

VSIDS and LBD belong to the radical learnt clause evaluation method. The description of the learnt clause is relatively simple. When the learnt clause is deleted periodically, some clauses that play a role in the search may be deleted by mistake.

The research on parallel solvers started late due to the development of computer hardware. Some representative parallel solvers have appeared in more than ten years, such as ManySAT [17], ppfolio2011 [18], PLingeling [19], TLingeling [20], Glucose-Syrup [21] and so on. They are essentially one of the three parallel processing principles: search tree partitioning, combinatorial parallelism, or hybrid both of them.

Some of the solvers are based on network exchange [22], and some solvers are based on database storage [23], and also some based on shared memory [12]. From the early sharing of all to the subsequent selective sharing, the learnt clause sharing strategy of the parallel solver is gradually formed.

Although the SAT solution has developed rapidly and the scale of the problems that can be dealt with has reached tens of millions, it still cannot meet the actual application needs. In the SAT Competition (2017), there were 350 benchmarks. The Champion Solver solved only 208 in the specified time. There are still 142 problems that cannot be solved [24] (a large part of the SAT Competition benchmarks comes from real industrial application problems).

The parallel solvers improve the efficiency of the SAT problem to some extent, but its capability is limited by the parallel hardware environment and other factors. In essence, it is necessary to study the effective SAT problem solving algorithm or improve the existing SAT solving algorithm. The description of the clauses of the learnt clause based on the length of the clause, VSIDS or LBD is not sufficient to fully quantify the role of the learnt clause in the search process.

This paper combines the simplified evaluation method based on the trend strength of learnt clauses with the LBD evaluation algorithm and proposes a mixed clause evaluation algorithm to describe the characteristics of the learnt clause more accurately. The key ideas are applied to Glucose4.1 and its parallel version of Syrup respectively by improving their evaluation algorithm part and the parallel node clause sharing strategy, aiming at enhancing the capability and efficiency the SAT solvers.

The remainder of the paper is organized as follows. The review of related works is provided in Section 2, including some brief overviews of relevant search algorithms and evaluation algorithms. Section 3 introduces the hybrid evaluation algorithm with focus on the serial version of SAT solver, while Section 4 proposes the improved clause sharing strategy for the parallel solver. The detailed experimental case studies and comparison analysis are provided in Section 5. The paper is concluded in Section 6.

2. RELATED WORKS

2.1. The DPLL Algorithm

The DPLL algorithm is an algorithm proposed by Davis, Putnam, Logemann and Loveland and named according to their name [5, 6]. The DPLL replaces the resolution part of the DP algorithm with branch backtracking. Essentially a depth-first traversal of a fully binary tree, looking for an assignment path so that all clauses are satisfied. When there is no unit clause or pure literal that can be used for Boolean constraint propagation, the algorithm selects a variable from the unassigned variables as a branch variable, assigns it to 1, and then traverses the branch. If there is a conflict (at least one clause cannot be satisfied), backtracking, assigning the branch variable to 0 and continue traversing.

The DPLL algorithm is a typical recursive algorithm [12], and the algorithm is described as follows:

  1. Execute the BCP and pure literal elimination algorithms until there are no unit clauses and pure literals in the clause set. If the branch is satisfied, the formula set can be satisfied. The current assignment is an example of the formula, and the algorithm ends. Otherwise, go to the next step.

  2. Select decision variables according to the strategy and perform the next step.

  3. Select the branch whose decision variable is assigned the value ”1” and execute the DPLL algorithm. If the branch can be satisfied, the formula set can be satisfied and the algorithm ends. Otherwise, go to the next step.

  4. Select the branch whose decision variable is assigned ”0”, and execute the DPLL algorithm. If the branch can be satisfied, the formula set can be satisfied and the algorithm ends. Otherwise, the current branch is executed and the current branch is not satisfied.

If the currently executing branch is the topmost branch, the entire algorithm ends and the clause set is unsatisfiable.

Figure 1 shows a partial example of a DPLL search algorithm, with blank nodes representing a certain decision of the algorithm. Up 0 means that the variable is assigned by Boolean constraint propagation. In this decision, variable x1 is assigned a value of 0 by Boolean constraint propagation. In the subsequent variable decision process, the DPLL algorithm does not utilize the known search information [12], and the same branch in the search space in the dotted line frame are repeatedly accessed.

Figure 1

An example of the assignment of DPLL.

2.2. CDCL Algorithm

In order to avoid the problem of repeated searches in the DPLL, Marques-Silva et al. first proposed the CDCL algorithm in the GRASP [7] solver. The purpose of retaining the assignment information when a conflict occurs is achieved.

The main improvement of CDCL algorithm compared with DPLL algorithm is [25]: analyzing the causes of conflicts by constructing implication graphs, constructing learnt clauses and putting them into the original clause set; non-recursive executing algorithms; instead of returning to the previous decision position, algorithm backtracking undoes the most recent assignments and the BCP implication assignments resulting from these assignments after analysis.

The classic CDCL algorithm [25] is described below

  1. Simplify the clause set and return when it can be satisfied by simplification.

  2. Check if all the literals have been assigned, and return if all clauses are satisfied. Otherwise, go to step 3.

  3. Select an unassigned variable as a decision variable based on the heuristic strategy.

  4. Execute the BCP process, if the conflict is found, go to step 5, otherwise skip back to step 2 and continue.

  5. Analyze the reason for the conflict, obtain the learnt clause and the backtracking decision level. If the backtracking level is 0, it means that it has been rolled back to the top level, and the founding value is not found, and the clause set is unsatisfied. Otherwise, perform step 6.

  6. Back to the specified level, undo all assignments from the current level to the backtracking level and undo assignments in the BCP process. Go to step 2.

2.3. The VSIDS Algorithm

The VSIDS evaluation algorithm is a classical algorithm in the SAT problem solving [13], which is described as follows:

The algorithm sets the activity attribute for each original clause, with the initial value set to 1. Cla_inc is the activity increment with an initial value of 1/0.999.

When a conflict occurs during the search, and if the clause is used for conflict analysis, its activity value activity=activity*cla_inc. When the activity value exceeds 10 [20], the activity value of all clauses is scaled by 10−20, and cla_inc is scaled to cla_inc*10−20.

At the end of each conflict analysis, adjust the activity increment, cla_inc=cla_inc*(1/0.999).

2.4. LBD Algorithm

LBD was first proposed by Gilles in the early version of Glucose (Champion, SAT Competition 2009 and 2011) [11] to evaluate the quality of the learnt clause. The value of LBD is the number of different decision levels in which the literals in a clause. The literals at the same decision level are considered to be a block, and a learnt clause links the literals on different blocks together.

Suppose there are two learnt clauses as follows:

C1=x1(6)∨x3(6)∨x4(3)∨x5(6)C2=x7(1)∨x8(5)∨x9(7)

The symbol x1(6) indicates that the variable x1 is assigned at the 6th decision level. Then the decision level set of the variable in clause C1 is {3, 6}, and its LBD value is 2. So, clause C2 has its variables from three decision levels with an LBD value of 3.

A clause with an LBD value of 2 is called a glue clause, such as the learnt clause C2 above. Because one of the literals comes from the decision level at which the conflict occurred, the other literals comes from another decision level. The glue clause is considered to be the best and most reserved clause. Glucose periodically deletes clauses with an LBD value greater than 2 to reduce the size of the learnt clauses.

2.5. Hybrid Evaluation Algorithm

The hybrid evaluation algorithm is a mixture of well-known evaluation algorithms.

Lingeling [16] uses the inner-outer scheme to manage learnt clauses, also known as reduce-schedule. In the Inner scheme, the evaluation method of LBD is adopted. When the distribution of the glue clause is not balanced, the clause evaluation method of the VSIDS is dynamically switched. The Outer scheme uses the Luby sequence to control the total number of learnt clauses. Such a scheme has proven to be very effective in well-structured example solving.

The outstanding contribution of the MapleCOMSPS solver is the learning rate branching heuristic (LRB) algorithm and the conflict history based branching heuristic (CHB) algorithm [26, 27]. The decision variables selected by these two algorithms can produce high-quality learnt clauses. At the same time, in the management of learnt clauses, MapleCOMSPS also uses the clause deletion strategy of LBD and VSIDS. In the first 2 500 seconds of the operation, the clause is evaluated by LBD. Then, use VSIDS evaluates learnt clauses [14]. Win the championship in the SAT competition (2016) Main group.

2.6. Clause Sharing Strategy

The “good” clause sharing strategy in the parallel solver can accelerate the parallel solution efficiency. The “bad” clause sharing strategy occupies communication bandwidth and increases the size of invalid learnt clauses of the database in each node, which is not conducive to solving the problem.

In the 2009 International SAT Competition, the Parallel Competition Group first appeared. The champion of parallel group, ManySAT [17] shared the learnt clause based on lockless queues, and the length of the shared learnt clauses ware limited to no more than 8.

In 2011, the parallel version of Lingeling, PLingeling and its variant TLingeling joined the shared equivalence structure based on the shared unit clause. These two versions of the parallel solver have been in the leading position in many years [16, 20].

Roussel O. developed a combined parallel solver named ppfolio by combining Minisat, zCharf, Lingeling and other solvers, while ppfolio provides only unit clause sharing function between these combined solvers [18]. Ppfolio is considered the benchmark for parallel solver efficiency.

Soos M. added parallel processing to CryptoMiniSat, using a lockless shared data structure, sharing unit clauses, learnt clauses, and “Xor” clauses between parallel nodes [28]. Ranked third in the SAT Competition (2016) in Parallel Group.

Audemard, G. proposed a lazy data exchange strategy [29], the generated learnt clauses are not immediately shared, only the clauses that are used once in the conflict analysis will be shared. It also limits the LBD value of the shared clause and limits the length of the clause. When the parallel node imports the external learnt clause, only the clause with the LBD value less than 2 and the unit clause being monitored are imported. The improved Glucose parallel version won the first place in the parallel group between the 2015 and 2017 SAT competitions [30].

3. SIMPLIFIED TREND STRENGTH AND LBD HYBRID EVALUATION ALGORITHM

3.1. Trend Strength Evaluation Algorithm

We tested and analyzed the examples of the SAT Competitions (2015 and 2016) and found that: 84% of the learnt clauses were deleted by the solver based on the VSIDS evaluation method; the solver which used LBD method removes 80% of the learnt clauses.

The earliest generated learnt clauses account for less and less in the subsequent search process. Both VSIDS and LBD clause evaluation methods adopt stricter deletion strategies, and the utilization rate of learnt clauses is not high.

The trend strength evaluation algorithm quantifies the trend strength of the learnt clauses used for conflict analysis.

Definition 1.

Conflicts number ti(i>=0) indicates the total number of conflicts that occurred during search, corresponding to the i-th the learnt clause C being applied to the conflict analysis. In particular, t0 represents the total number of conflicts when the learnt clause C was generated.

Definition 2.

Conflicts interval Δti indicates that the total number of conflicts of the i-th the learnt clause C is applied to the conflict analysis compared with the previous one. The specific calculation method is as follows:

Δti=0(i=0)ti−ti−1(i≥1)

By Definition 2, it can be concluded that the smaller the Δt, the more frequently the clause is used.

Definition 3.

Local trend Ti is the quantitative value of the change trend of the frequency of learnt clauses being used. The specific calculation method is as the Eq. (2) shown.

Ti=1, iff(Δti−Δti−1)<0;0, iff(Δti−Δti−1)=0;(i≥2)−1, iff(Δti−Δti−1)>0;

It indicates that the frequency of the clause being used is increased if Ti = 1, and so the trend is enhanced. If Ti = 0, it indicates that it is not used during the conflict period. Ti = −1 means that the interval used in the period becomes larger and the tendency becomes weaker.

For clause C, the general trend Gk(C) in the k-th period can be obtained from the local trend accumulation.

G(C)=0(i≤1)∑​ki=2Ti(2≤i≤k)

We first incorporates this algorithm into the MiniSat solver and tests it with the cases in the SAT Competition (2015 and 2016). In the best case, the Trend strength evaluation algorithm is better than VSIDS and worse than LBD.

Although the trend strength can describe the trend change of the clause applied to the conflict analysis, its calculation method is more complicated than the number of times the clause is used. The simplified version only needs to save the number of times the learnt clause is used for conflict analysis.

3.2. Simplified Trend Strength and LBD Hybrid Evaluation Algorithm

The simplified trend strength algorithm is a shorten version of trend strength algorithm. It only save the number of times of the learnt clause. In order to implement this, we introduce a function which named “UsageCount”. The “UsageCount” function is mainly responsible for updating the conflicts number of a learnt clause which corresponding to “usedCount” (a member of the clause object).

The simplified trend strength and LBD hybrid algorithm is based on the LBD algorithm and adds the “UsageCount” function of the learnt clause in conflict analysis. In terms of data structure, the “usedCount” member is added to the clause structure, and the “usedCount” counter value is increment by one each time the learnt clause participates in the conflict analysis by “UsageCount” function.

Periodically deleting the learnt clause module in Glucose corresponds to the reduceDB() function. The LBD restriction is replaced by the “usedCount” restrictions. As it shown in rhombuses in Figure 2.

Figure 2

Flow chart of reduceDB().

4. IMPROVED CLAUSE SHARING STRATEGY IN PARALLEL SOLVER

4.1. The Clauses Strategy of Syrup

4.1.1. The shared data structures

Syrup is essentially a multi-threaded parallel solver. All children threads share learnt clauses and implement data synchronization between threads through locks.

The MultiSolvers class manages ParallelSolver classes, maintains and runs multiple threads in parallel. At the same time, it relies on SolverCompanion and its subclass ShareComparion to manage the learnt clauses sharing.

The UML class diagram is shown in Figure 3.

Figure 3

Class diagram of syrup.

4.1.2. Export and import of learnt clauses

Syrup is more cautious in dealing with clause sharing between parallel nodes. It considers that clauses with LBD value less than 8 and clause length less than 40 to be “good” clauses and should be shared. Second, in order to avoid mutual interference between nodes. In the initial time of running, it is forbidden to share the learnt clause until the number of conflicts of the node reaches 5 000 times.

It performs a lazy clause sharing strategy. Before the clause is shared, it observes the number of times it is applied to the conflict analysis. Only the clauses that appear in conflict analysis can be shared. Consistent with the strategy in the serial version, the LBD value of the clause that restricts sharing is less or equal to 8, and the length of the clause is less than 40, and the unit clause is directly shared.

If the number of conflicts has reached 5 000 during the search, the import operation of the external learnt clauses can be performed. First import the unit clauses and then import other learnt clauses that meet the evaluation criteria.

4.2. Clause Sharing Strategy Using the Hybrid Evaluation Method

During the execution of the search function of the parallel node, if there is a conflict, the analyze function will analyze the cause of the conflict and obtains the learnt clause. If the learnt clause is a unit clause, it will be directly shared with the shared memory queue. It judges whether to share the current learnt clause or not according to the clause sharing strategies. Algorithm 1 is a clause sharing strategy in the hybrid evaluation mode, and the number of times the clause is used as a condition to replace the original partial LBD constraint.

The second line of bold code replace the original LBD evaluation condition, and derives the clauses with the highest frequency of use, or derives the best learnt clauses considered by the LBD algorithm—“glue” clause. “LimitNum” indicates the threshold of the number of times the learnt clause is used whose value needs to be set according to the experimental results.

Algorithm 1. Parallel Export Learnt Clause

5. EXPERIMENTAL CASE STUDIES

Glucose is an internationally renowned CDCL solver. The author's main contribution is to propose an LBD evaluation algorithm and successfully apply it to the solver. Glucose has won numerous awards in the SAT International Competition. The SAT competition (2016) even set the Glucose-Hack award outside of the Main Track group. Based on Glucose 4.1 and its parallel version of Syrup, this paper uses the hybrid clause evaluation method to improve in reduceDB() function and the clause shared strategy in parallel node.

The versions of the SAT solvers and the software environment and hardware environment of the test machines are shown in Table 1 and Table 2.

OS Software CPU Memory
Win7
x64		 Cygwin64
GCC6.4.0		 Intel®Core™ i7-4790 CPU @3.60 GHz 3.6 GHz 16 G
Table 1

Operation environment.

Solver Description
Glucose Serial version
Syrup Glucose parallel version
Glucose-H Added hybrid clause evaluation strategy
Syrup-H Added hybrid clause evaluation strategy, unchanged parallel clause sharing strategy
Syrup-HE Added hybrid clause evaluation strategy, changed parallel clause sharing strategy
Syrup-HEN40 Added hybrid clause evaluation strategy, changed the parallel clause sharing strategy, but removed the limitation that the length of the shared learnt clause does not exceed 40.
Table 2

Versions of SAT solvers.

We use 350 benchmarks of the MainTrack group of the SAT Competition (2017), with a time limit of 3 600 seconds. All test machines strictly guarantee the same software and hardware environment. According to the results of previous experimental analysis, Glucose-H achieved the best results when the value of LimitNum was 150. The same values are used in the parallel version, and for each test case is runs 5 times, and the average is taken as the statistical result.

First, ran Glucose and Glucose-H based on the hybrid clause evaluation strategy. The results are shown in Table 3. The evaluation strategy based on the hybrid learning clause is 3 more than the original version on SAT, and 1 less than the original version on UNSAT. There are 2 more overall, and the average time is 28.5 seconds less than that of Glucose.

Solvers SAT UNSAT Total Avg-time(s)
Glucose 86 99 185 749.694
Glucose-H 89 98 187 721.121
Table 3

Results of glucose and Glucose-H.

The results are highly coincident in the time distribution of the first 80 questions, so the abscissa starts from 80. In Figure 4, Sum represents the number of solving problems, and the ordinate axis represents the time taken for solving a single problem. It is obvious from the figure that the Glucose-H based on the hybrid evaluation algorithm represented by the red triangle is significantly less time-consuming than Glucose, especially in the 150–180 range.

Figure 4

The relationship of used times and results.

In the parallel version of the experiment, we used the same configuration of Syrup in the SAT Competition, running 24 threads in parallel by default. In order to analyze the influence of the hybrid clause evaluation and clause sharing strategy on the solution results, different combinations are set up to form different parallel solvers. The parallel solvers involved in the comparative analysis are named after the Syrup prefix. See Table 2 for details.

The results of the parallel experiments are shown in Table 4. It can be seen that the number of solving problems of each version based on the hybrid clause evaluation strategy is more than Syrup, which shows the effectiveness of the hybrid learning clause evaluation method. On the other hand, the version of Syrup-HE with a hybrid clause sharing strategy is 1 less than the results of Syrup-H which only use the hybrid clause evaluation algorithm, but the number of UNSAT solved by it is 100, and more than other versions.

Solvers SAT UNSAT Total Avg-time(s)
Syrup 97 95 192 634.031
Syrup-H 99 99 198 707.568
Syrup-HE 97 100 197 713.459
Syrup-HEN40 96 98 194 706.111
Table 4

Results of parallel solvers.

When Syrup-HEN40 shares the learning clause, it removes the restrictions that the learnt clauses must be less than 40 in length so they can be shared. The results are 3 less than Syrup-HE, which reduces the efficiency of the solution. This also confirms the rationality of the length limit of learnt clauses in [31].

Figure 5 shows the relationship between the results and time distribution. From the relationship between the number and the time distribution curve, although average time consumption of the improved version is more than Syrup, the solution problems are concentrated on the more difficult problems. On the last few difficult problems, the red triangle representing Syrup-HE is lower than the other lines, indicating that it takes less time than several other solvers.

Figure 5

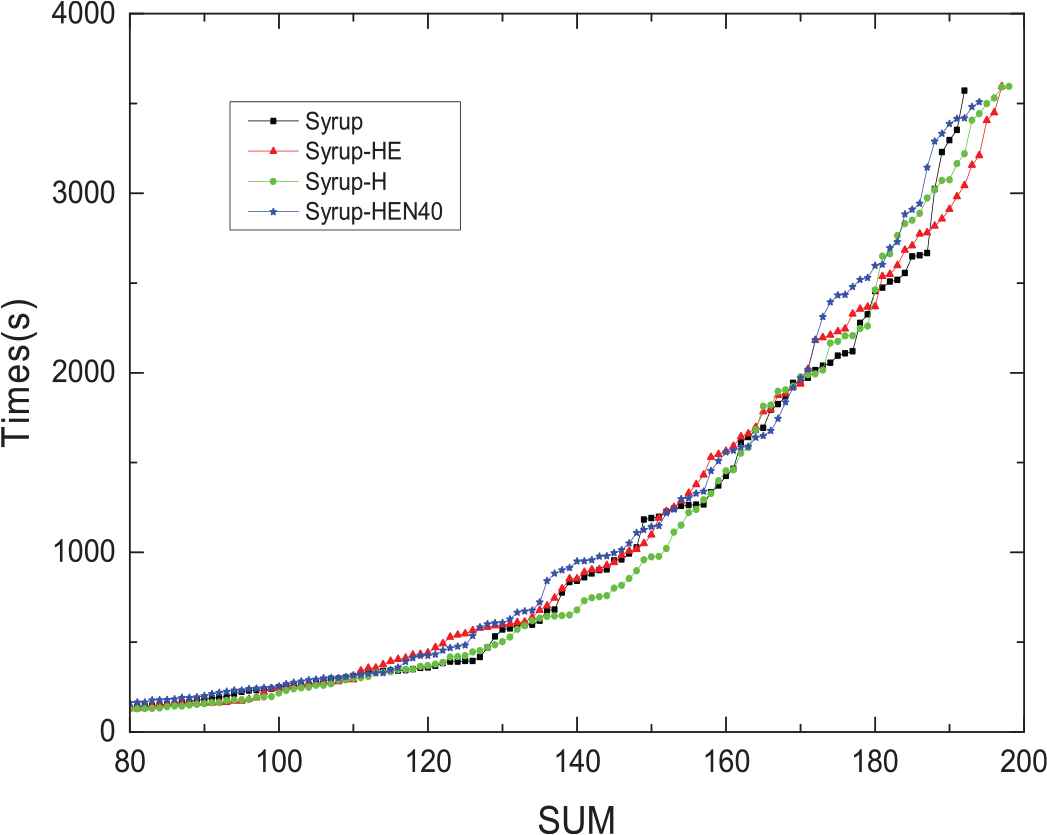
The relationship of used times and results for parallel version solvers.

There are 166 records that are the intersection of results of Glucose, Syrup, and Syrup-HE. After eliminating the noise data with relatively large difference between the two times, the corresponding acceleration ratio data distribution is shown in Figure 6. The red left slash shades to indicate a parallel solver based on the hybrid clause evaluation and hybrid sharing strategy, and the blue right slash shaded area represents Syrup. The red shaded area is larger than the blue shaded area, indicating that the Syrup-HE has a higher speedup than the original program at the same number of threads.

Figure 6

The speed-up ratio of Syrup-HE and Syrup.

In a given hardware environment, the performance of parallel programs does not always increase with the number of threads. In order to study the relationship between the number of threads and the number of problems solved, the results of the execution under different number of threads of Syrup and Syrup-HE are shown in Table 5.

TN Syrup Syrup-HE
SAT UNSAT SUM SAT UNSAT SUM
4 95 110 205 88 106 194
8 97 111 208 97 111 208
12 97 106 203 95 106 201
16 95 103 198 93 107 200
20 97 99 196 94 102 196
24 97 95 192 97 100 197
Table 5

Results of Syrup and Syrup-HE with different TNs (thread numbers).

When the number of threads is 8, both solvers reach the peak value of the number of problems solved, and then the number of solutions decreases as the number of threads increases. At the same time, although the number of solving problems is exactly the same when the number of threads is 8, the problems solved are not the same. There are seven problems that have not been solved by Syrup-HE.

We also tested the solvers with 400 benchmarks in the SAT Competition 2018 at the same environment except that the thread number is set to 8. The result is shown in Figure 7. Obviously, for the test data of 2018, the improved version of the parallel solver is still more efficient than the original. For Syrup-H, there are 6 more solutions than the Syrup.

Figure 7

The relationship of used times and results for parallel version solvers (thread number = 8).

6. CONCLUSIONS

In this paper, the hybrid learning clause evaluation algorithm has been proposed and applied to improve Glucose and its parallel version of Syrup (the champion of parallel group in SAT Competition 2017). The experimental case studies and comparisons have shown that the hybrid evaluation method can reach and exceed the solution efficiency of the SAT solvers which are only based on the LBD evaluation algorithm to a large extent.

The downside is that the parameter settings in the hybrid evaluation algorithm are based on statistical analysis, and the intrinsic relationship needs further investigation, although most existing clause evaluation algorithms have this kind of shortage.

Follow-up research will consider the specific problem type, analyze the relationship between the frequency of the usage of the learnt clause and the problem itself, in order to find the patterns between parameters and the problem types, with the expectation to solve more problems within the specified time.

ACKNOWLEDGEMENTS

This work is supported by the National Natural Science Foundation of P. R. China (Grant No.61673320) and the Fundamental Research Funds for the Central Universities (Grant No.2682018ZT10, 2682018CX59, 2682018-ZT25). The authors also gratefully acknowledge the helpful comments and suggestions of the teachers and students from National-Local Joint Engineering Laboratory of System Credibility Automatic Verification at Southwest Jiaotong University in China, and especially appreciate that the Lab provides the testing PC equipment.

REFERENCES

1.S.A. Cook, The complexity of theorem proving procedures, in Proceeding of 3rd Annual ACM Symposium on Theory of Computing (New York), 1971, pp. 151-158.
2.E. Clarke, A. Biere, R. Raimi, and Y. Zhu, Bounded model checking using satisfiability solving, Form. Method. Syst. Des., Vol. 19, No. 1, 2001, pp. 7-34.
3.Y. Vizel, G. Weissengbcher, and S. Malik, Boolean satisfiability solvers and their applications in model checking, Proc. IEEE., Vol. 103, No. 11, 2015, pp. 2021-2035.
4.L. Kuper, G. Katz, J. Gottschlich, K. Julian, C. Barrett, and M. Kochenderfer, Toward Scalable Verification for Safety-Critical Deep Networks, arXiv preprint arXiv: 1801.05950, 2018.
5.M. Davis and H. Putnam, A computing procedure for quantification theory, J. ACM., Vol. 7, No. 3, 1960, pp. 201-215.
6.J. Franco and M. Paull, Probabilistic analysis of the Davis Putnam procedure for solving the satisfiability problem, Discrete Appl. Math., Vol. 5, No. 1, 1983, pp. 77-87.
7.J.P. Marques-Silva and K.A. Sakallah, GRASP: a search algorithm for propositional satisfiability, IEEE Transac. Comput., Vol. 48, No. 5, 1999, pp. 506-521.
8.M.W. Moskewicz, C.F. Conor, Y. Zhao, L. Zhang, and S. Malik, Chaff: engineering an efficient SAT solver, in Proceedings of the 38th annual Design Automation Conference (ACM, New York, 2001), pp. 530-535.
9.N. Een and N. Sorensson, An extensible SAT-solver, Theory and Applications of Satisfiability Testing, Springer, Berlin, Heidelberg, 2004, pp. 502-518.
10.J. Marques-Silva, I. Lynce, and S. Malik, Conflict-driven clause learning SAT solvers, A. Biere, M. Heule, H. van Maaren, and T. Walsh (editors), Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, IOS Press, The Netherlands, 2009, pp. 131-153.
11.G. Audemard and L. Simon, Glucose: A solver that predicts learnt clauses quality, SAT Competition, Swansea, Wales, United Kingdom, June 30–July 3 2009, pp. 7-8.
12.T. Ehlers, SAT and CP-Parallelisation and Applications, Universitätsbibliothek Kiel, Germany, 2017.
13.N. Sorensson and N. Een, Minisat v1.13- A SAT solver with conflict-clause minimization, SAT Competition, Vol. 2005, No. 53, 2005, pp. 1-2.
14.J.H. Liang, C. Oh, V. Ganesh, K. Czarnecki, and P. Poupart, Maple-COMSPS, MapleCOMSPS LRB, Maple COMSPS CHB, SAT Competition Bordeaux, France, 2016, pp. 52.
15.A. Biere, P{re, i}coSAT, SAT Competition, Swansea, Wales, United Kingdom, June 30–July 3 2009, pp. 41-43.
16.A. Biere, Lingeling and friends entering the SAT challenge 2012, in Proceedings of SAT Challenge (2012), pp. 33-34.
17.Y. Hamadi, J. Said, and S. Lakhdar, ManySAT: a parallel SAT solver, J. Satisfiability Boolean Model. Comput., Vol. 6, 2008, pp. 245-262.
18.O. Roussel, Description of ppfolio, in Proceeding of SAT (Trento, Italy, June 17–20, 2012), 2011, pp. 46.
19.A. Biere, Lingeling, plingeling, picosat and precosat at sat race 2010, FMV Rep Ser. Tech. Rep., Vol. 10, No. 1, 2010, pp. 1-4.
20.A. Biere, Splatz, Lingeling, PLingeling, Treengeling, YalSAT Entering the SAT Competition, in Proceedings of SAT Competition (2016), 2016, pp. 44-45.
21.G. Audemard and L. Simon, Glucose and Syrup in the SAT Race 2015, SAT Race, Austin, Texas, USA, 24–27 September 2015.
22.W. Chrabakh and R. Wolski, GridSAT: a system for solving satisfiability problems using a computational grid, Parallel Comput., Vol. 32, No. 9, 2006, pp. 660-687.
23.M. Lewis, T. Schubert, and B. Becker, Multithreaded SAT solving, in Design Automation Conference (ASP-DAC'07 (Asia and South Pacific IEEE 2007)), 2007, pp. 926-931.
24.M. Heule, M. Jarvisalo, and T. Balyo, Results page of SAT Competition 2017, 1 Sept. 2017. Retrieved September 20, 2018, from https://baldur.iti.kit.edu/sat-competition-2017/index.php?cat=results
25.K. Claessen, N. Een, M. Sheeran, and N. Sorensson, SAT-solving in practice, Discrete Event Systems, WODES 2008, in 9th International Workshop on IEEE, 2008, pp. 61-67.
26.J.H. Liang, V. Ganesh, P. Poupart, and K. Czarnecki, Learning rate based branching heuristic for SAT solvers, in Proceedings of the 19th International Conference on Theory and Applications of Satisfiability Testing (Springer, Cham), 2016.
27.J.H. Liang, V. Ganesh, P. Poupart, and K. Czarnecki, Exponential recency weighted average banching heuristic for SAT solvers, AAAI, 2016, pp. 3434-3440.
28.M. Soos, The CryptoMiniSat 5 set of solvers at SAT Competition 2016, SAT Competition, Bordeaux, France, 2016, pp. 28.
29.G. Audemard and L. Simon, Lazy clause exchange policy for parallel SAT solvers, in Theory and Applications of Satisfiability Testing – SAT 2014 – 17th Internation Conference (Vienna, Austria), 2014.
30.A. Gilles and L. Simon, On the Glucose SAT solver, Int. J. Artif. Intell. Tools., Vol. 27, No. 1, 2018, pp. 1840001.
31.Z.H. Fu, M. Yogesh, and M. Sharad, New features of the SAT04 versions of zChaff, SAT Competition 2004, Solver Descriptions, 2004.
<Previous Article In Issue
Download article (PDF)
Next Article In Issue>
Journal
International Journal of Computational Intelligence Systems
Volume-Issue
12 - 1
Pages
250 - 258
Publication Date
2018/11/19
ISSN (Online)
1875-6883
ISSN (Print)
1875-6891
DOI
10.2991/ijcis.2018.125905645How to use a DOI?
Copyright
© 2019 The Authors. Published by Atlantis Press SARL.
Open Access
This is an open access article distributed under the CC BY-NC 4.0 license (http://creativecommons.org/licenses/by-nc/4.0/).

Cite this article

risenwbib
TY  - JOUR
AU  - Guanfeng Wu
AU  - Qingshan Chen
AU  - Yang Xu
AU  - Xingxing He
PY  - 2018
DA  - 2018/11/19
TI  - A Hybrid Learnt Clause Evaluation Algorithm for SAT Problem
JO  - International Journal of Computational Intelligence Systems
SP  - 250
EP  - 258
VL  - 12
IS  - 1
SN  - 1875-6883
UR  - https://doi.org/10.2991/ijcis.2018.125905645
DO  - 10.2991/ijcis.2018.125905645
ID  - Wu2018
ER  -