A comparative study on the mechanical properties of the umbilical vein and umbilical artery under uniaxial loading
- DOI
- 10.1016/j.artres.2014.02.001How to use a DOI?
- Keywords
- Umbilical vein; Umbilical artery; Mechanical properties; Hyperelastic; Constitutive modeling
- Abstract
Purpose: Coronary Artery Disease (CAD) is the main cause of mortalities worldwide. The Saphenous Vein (SV) and Umbilical Vein (UV) are the most common veins using for treatment as a Coronary Artery Bypass Graft (CABG). The mechanical properties of UV owing to its long-term patency for CABG are deemed important. However, there is a lack of knowledge on the mechanical properties of UV. In this study, the linear (Young’s modulus and maximum stress) and nonlinear (hyperelastic material coefficients) mechanical properties of 8 human umbilical vein and umbilical artery (UA) are investigated using a series of uniaxial tensile tests. The nonlinear mechanical behavior of UV/UA is computationally investigated using hyperelastic strain energy density functions, including Mooney-Rivlin and Ogden. A hyperelastic constitutive model is selected to best fit the axial behavior of the UV/UA.
Results: The results reveal that the Young’s modulus and maximum stress of UA are 342% and 19% more than that of UV, respectively. The Mooney-Rivlin material model is selected to represent the nonlinear behavior of the UV and UA which can be used in future biomechanical simulations of the umbilical vein and umbilical artery.
Conclusions: The higher mechanical properties of umbilical artery compared to umbilical vein might have related to the amount of elastin and collagen content on the UA wall. The results of this study could be utilized to understand the extension and rupture mechanism of UV and UA, and has implications for interventions and surgeries, including balloon-angioplasty, bypass, and stenting.
- Copyright
- © 2014 Association for Research into Arterial Structure and Physiology. Published by Elsevier B.V. All rights reserved.
- Open Access
- This is an open access article distributed under the CC BY-NC license.
Introduction
Coronary Artery Disease (CAD) is responsible for almost 30% of all mortalities worldwide.1–4 The most common treatment for CAD is bypass surgeries which usually a human Saphenous Vein (SV) or Umbilical Vein (UV) are employed for.5 During parental development, the umbilical cord is physiologically and genetically part of the fetus and in humans normally contains a pair of arteries and a vein.6,7 The umbilical vein supplies the fetus with oxygenated, nutrient-rich blood from the placenta. Conversely, the fetal heart pumps deoxygenated, nutrient-depleted blood through the umbilical arteries (UA) back to the placenta.8,9
The mechanical properties of umbilical vein and umbilical artery have a key asset in their long-term performance as the natural implant in Coronary Artery Bypass Graft (CABG). In addition, the mechanical properties of human UV and UA can be incorporated to hemodynamic studies of UV/UA and would lead to more precise hemodynamic outcomes. In most computational models, arterial wall is considered to be rigid, and, as a result, the velocity profile was found to be partially blunted and skewed.10 The mechanical properties of fetal veins are not known, and computations with elastic walls and pulsatile flow have so far not been attempted. Once information on the mechanical properties of the UV and UA is available, the wave propagation can be addressed in a mathematical model, and a more meaningful interpretation of various clinical findings can be expected. Hellevik et al.,11,12 characterized the mechanical properties of UV using animal samples. They only measured the linear elastic parameters which clearly cannot address the nonlinear behavior of human UV. Recently, the nonlinear hyperelastic mechanical properties of human UA in preeclampsia have been computed using a series of uniaxial extension tests.13 Nonetheless, there is still a lack of knowledge on the linear (Young’s modulus and maximum stress) and nonlinear (hyperelastic material coefficients) mechanical properties of human UV and UA. To address this issue, it is important to conduct sufficient tests for the nonlinear calibrations and verification of suitable mathematical constitutive models under general axial states of stresses.14 To date, most studies regarding the characterizing the mechanical properties of UV for the purpose of bypass surgeries have been concentrated on the linear elastic properties.12,15 Hyperelastic behavior of UV is deemed important as coronary artery mechanical behavior is almost entirely nonlinear.1–3 Thus, it seems necessary to design a setup to measure the mechanical properties of human UV/UA by considering nonlinear behavior.
This study is aimed to experimental and analytical characterization of the linear elastic and nonlinear hyperelastic mechanical behavior of human UV and UA under uniaxial loading candidates for bypass surgeries. Two independent hyperelastic models, i.e., Mooney-Rivlin and Ogden, are implemented for the nonlinear response of umbilical tissues. Proposed hyperelastic models are calibrated from the experimental results and used to predict the mechanical response of the UV/UA under general axial stress states.
Materials and methods
Materials and specimen preparation
The UV and UA were removed after cesarean from eight individuals. All materials removal was excised with permission of donators under the ethical rules of Tehran University of Medical Sciences (TUMS). The veins and arteries were removed and cleaned from the surrounding tissues subsequently. In order to minimize tissue degradation, portions of the veins and arteries immediately were preserved in solution of 0.90% w/v of NaCl at 4–5 °C before the uniaxial tensile test. The testing material was obtained by cutting 15 mm long branchless segment of veins and arteries.
Experimental setting and tensile test
The outer diameter, initial wall thickness, and length of the segments of umbilical veins and umbilical arteries were measured precisely using digimatic ruler having a resolution of 0.005 mm ± 0.05% (Insize, Vienna, Austria) and listed in Table 1. The tensile test was performed using a uniaxial tensile test apparatus adapted for testing biological specimens used in our previous studies.16–19 The specimens were taken out from the physiological saline right before the test and mounted on the tensile test machine. The tests were carried out at sufficient extra relative humidity to prevent the specimens from drying. The consistent spray of physiological saline was also used for the same reason. Preconditioning of soft tissues has become a common procedure in tensile testing to assess the history dependence of soft tissues. Therefore, ten cyclic preconditioning with a suitable pre-load based on uniaxial experimental results is applied to each UV and UA before any measurement begin. The sample’s length was measured after the application of the pre-load. Force was, then, applied to each specimen and the linear (elastic modulus and maximum stress) and nonlinear (hyperelastic material coefficients) mechanical properties of each sample was measured before the failure occurred. A low strain rate of 5 mm/min which is typical for surgical procedures and gives more insight into tissue behavior was employed by the action of an axial servo motor.3,20,21
| Sample number | Age (year) | Outer diameter (mm) | Inner diameter (mm) | Initial length (mm) | |
|---|---|---|---|---|---|
| 1 | Umbilical vein | 24 | 4.92 | 3.97 | 15 |
| Umbilical artery | 3.01 | 2.42 | 15 | ||
| 2 | Umbilical vein | 25 | 4.95 | 3.96 | 15 |
| Umbilical artery | 2.99 | 2.46 | 15 | ||
| 3 | Umbilical vein | 25 | 4.96 | 3.89 | 15 |
| Umbilical artery | 3.00 | 2.47 | 15 | ||
| 4 | Umbilical vein | 26 | 4.95 | 3.92 | 15 |
| Umbilical artery | 3.02 | 2.48 | 15 | ||
| 5 | Umbilical vein | 28 | 4.98 | 3.94 | 15 |
| Umbilical artery | 3.01 | 2.50 | 15 | ||
| 6 | Umbilical vein | 29 | 4.93 | 3.97 | 15 |
| Umbilical artery | 2.97 | 2.51 | 15 | ||
| 7 | Umbilical vein | 31 | 4.87 | 3.90 | 15 |
| Umbilical artery | 2.99 | 2.45 | 15 | ||
| 8 | Umbilical vein | 34 | 4.96 | 3.95 | 15 |
| Umbilical artery | 2.95 | 2.48 | 15 |
The age and dimensions of umbilical veins and umbilical arteries samples.
Constitutive equations-strain energy density functions
The uniaxial experimental data was used to calibrate isotropic hyperelastic strain energy density functions (SEDFs) in order to generate multi-axial stress–strain relations that can be used in future finite element simulations of umbilical veins and umbilical arteries. Under the assumption that UV and UA are isotropic materials, it was possible to fit a general polynomial isotropic SEDF form (Eq. (1)). Two different isotropic SEDF models were examined: Mooney–Rivlin (Eq. (2)) and Ogden (Eq. (3)). The Mooney-Rivlin4,22 is special cases of the polynomial SEDF while the Ogden23 can be also considered as a polynomial form in terms of the stretch ratios as its variables instead of the invariants. The polynomial along with the other specialized forms of the SEDFs can be written as:
It should be noted that the above SEDFs are composed from two sums. The first is related to the uncompressive part of the function using the first and second invariants, while the second sum is for the compressive part of the SEDF using the third strain invariant. Linear least squares fit has been used for the Mooney-Rivlin model calibration, and nonlinear least squares fit was applied to match the constant for the Ogden model.
Statistical analysis
Data were first analyzed by analysis of variance (ANOVA); when statistical differences were detected, student’s t-test for comparisons between groups was performed using SPSS software version 16.0 (SPSS Inc., Chicago, IL, USA). Data are reported as mean ± std at a significance level of p < 0.05.
Results and discussions
The most common treatment for CAD is bypass surgeries which usually a human Saphenous Vein or Umbilical Vein are employed for.5 Many studies have used linear elasticity to measure the mechanical properties of UV.12,15 However, for large displacements and/or strains, these models might not be valid, and the non-linear stress–strain characteristics of these tissues must be considered.24 With that in mind, the purpose of this study was to quantify the hyperelastic mechanical properties of UV and UA intended for use as bypass grafts in CABG.
The (a) umbilical vein and (b) umbilical artery during uniaxial test are illustrated in Fig. 1. The uniaxial tensile test machine is consisted of a fix and moveable jaw which provides us with constant strain rate. The stress–strain diagrams for (a) UV and (b) UA under uniaxial loading are indicated in Fig. 2. The comparative histogram representation of the Young’s modulus and maximum stress for UV and UA is indicated in Fig. 3. The Young’s moduli of UV and UA are 2.67 and 9.98 MPa, respectively. This is entirely in agreement with13 which showed the Young’s modulus of 2.78 MPa for human umbilical artery. The maximum stress of UA is 19.05% more than that of UV (Fig. 3). The results show that the Young’s modulus of umbilical artery is significantly higher than that of umbilical vein (342.67%). This stiffness is believed to be related to the amount of elastin and collagen in UV which are considered as the most important components in arterial wall.3,13,15 Hayashi et al.25 stated that a simple constitutive relation, such as an exponential or logarithmic mechanical properties of soft biological tissues, is more advantageous than the more elaborated relations based on strain energy functions. In these simple formulations the numbers of coefficients are reduced, while their physical meaning is retained. From a practical point of view, expressing the elastic properties by a single parameter is more useful than a thorough but more composite expression based on several parameters.26,27 However, it should be noted that such linear mechanical properties cannot address the nonlinear mechanical behavior of most soft tissues, especially UV and UA, and using nonlinear material models based on SEDFs is deemed important for precise simulation and modeling results.12 Results from the tensile experimental tests were used to calibrate the SEDF candidates used for axial constitutive modeling. The experimental data were used to fit the incompressible part of the SEDF. Material constants for each SEDF candidate are listed in Tables 2 and 3. The plotted representative test result is the average values generated from all samples at their last loading cycle. Different range of ability to match the experimental test results is demonstrated by these functions (Fig. 2). Mooney-Rivlin and Ogden SEDFs were used to capture the nonlinear mechanical behavior of UV and UA. Mooney-Rivlin and Ogden material models shows nearly similar behavior and adequate ability to predict the UV behavior for most of the test data range. However, Ogden diverges from the Mooney-Rivlin at larger uniaxial strain magnitudes, especially for UA. The Mooney-Rivlin SEDF shows excellent ability to model the experimental stress–strain data for the entire range.28,29 The aim was to select a constitutive hyperelastic model for the UV and UA under uniaxial tensile loading. Therefore, the Mooney-Rivlin and Ogden functions seem to be more logical selection to represent the mechanical behavior of UV and UA where incompressible behavior is expected for higher hydrostatic stretch values. The Mooney-Rivlin function is select as the most material model to define the nonlinear mechanical behavior of UV and UA compared to the Ogden material model.

The (a) umbilical vein and (b) umbilical artery during uniaxial tensile test.
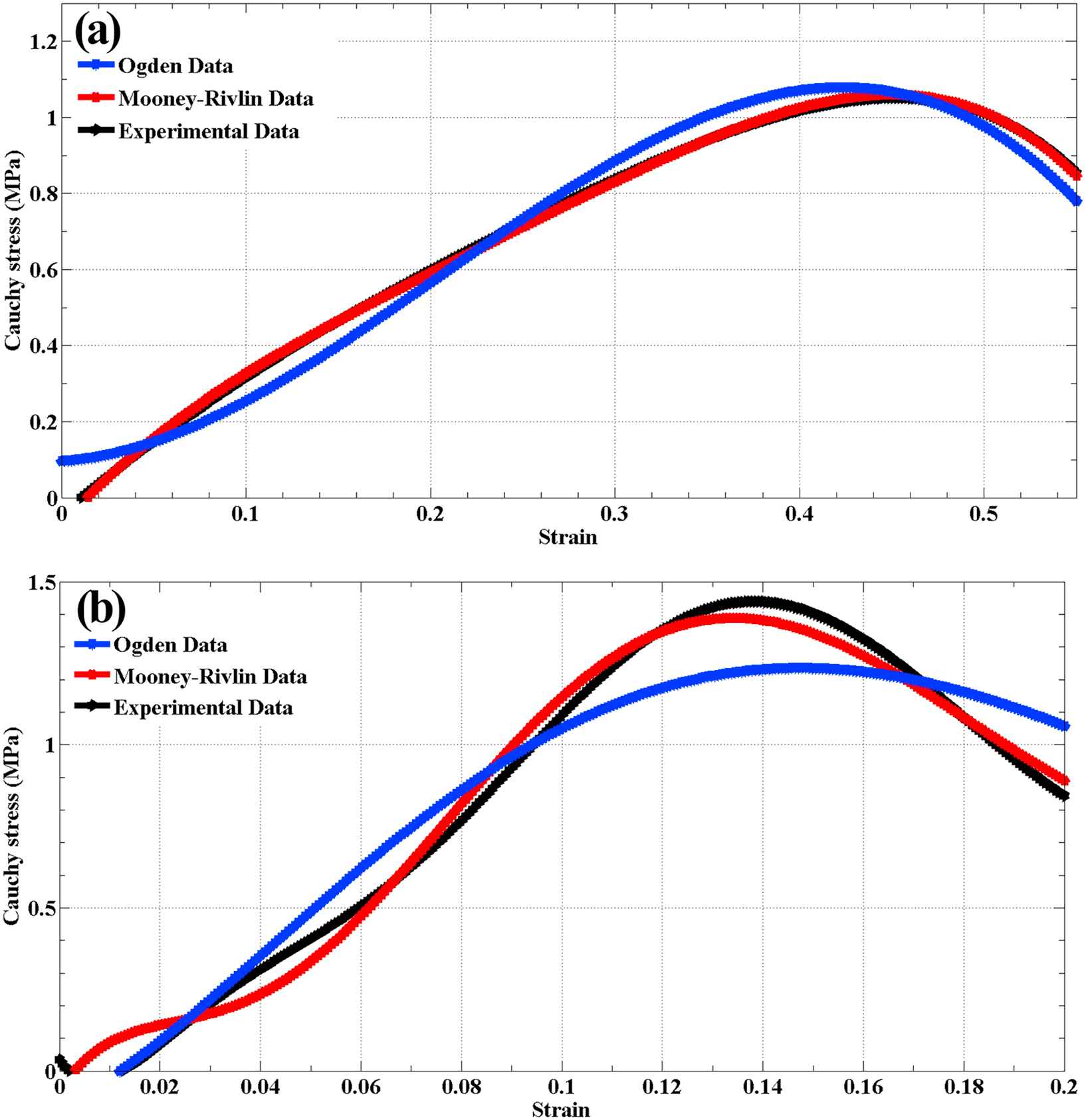
The comparative stress–strain diagrams of the (a) umbilical vein and (b) umbilical artery along with the data for the Mooney-Rivlin and Ogden hyperelastic models.
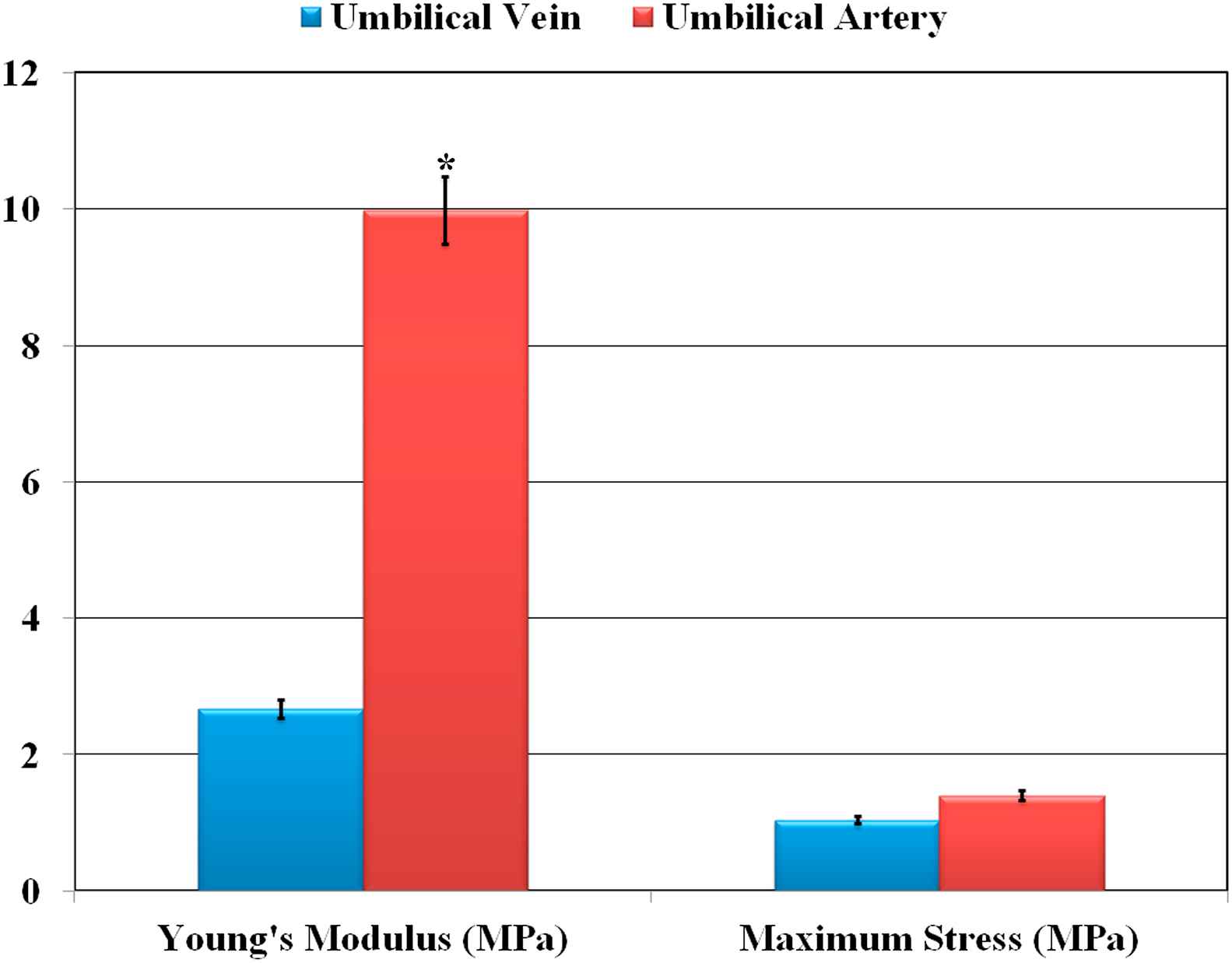
A histogram representation of Young’s modulus and maximum stress of umbilical vein and umbilical artery. *p < 0.05 compared to the Young’s modulus of umbilical vein.
| Umbilical vein | Material constants (MPa) | |||
| Hyperelastic model | C10 | C01 | ||
| Mooney-Rivlin | 0.89 | −0.42 | ||
| Umbilical vein | Material constants (MPa) | |||
| Hyperelastic model | μ1 | μ2 | α1 | α2 |
| Ogden | 3.16 | −2.94 | 3.71 | −11.89 |
Hyperelastic material coefficients of umbilical vein.
| Umbilical artery | Material constants (MPa) | |||
| Hyperelastic model | C10 | C01 | ||
| Mooney-Rivlin | −12.93 | 14.77 | ||
| Umbilical artery | Material constants (MPa) | |||
| Hyperelastic models | μ1 | μ2 | α1 | α2 |
| Ogden | −51.40 | 55.09 | −3.39 | −7.21 |
Hyperelastic material coefficients of umbilical artery.
Results presented in the current study may have implications for hemodynamic studies. Most investigations on the mechanical properties of the arteries have adopted a rigid artery wall assumption which could be acceptable for clinical studies of CABG,30 small arteries (<6 mm), and coronary laminar flow simulations.31 This is an incorrect assumption since the pulsatility affects the structure of the artery wall and causes deformation by the cyclic hemodynamics forces, particularly for the larger arteries, such as coronary, that show significant adaptation to these forces.2,32 Hence, the incorporation of the linear elastic and nonlinear hyperelastic parameters provided in this study instead of rigid wall assumption for the large arteries can have clinical relevance and can demonstrate the effects of hemodynamic forces on the structural changes.31 The reported mechanical properties also can be used to calculate pulse velocity and compliance in the human UV and UA.
Conclusions
This study investigated the mechanical properties of human umbilical vein and umbilical artery using a uniaxial tensile test instrument. The findings revealed that the elastic modulus and maximum stress of UA are higher than that of UV. The higher mechanical properties of umbilical artery compared to umbilical vein might have related to the amount of elastin and collagen content on the UA wall. We also captured the nonlinear mechanical behavior of UV and UA through strain energy density functions, including Mooney-Rivlin and Ogden. The Mooney-Rivlin and Ogden well fitted with the experimental data of UV, whereas UA fitted with Mooney-Rivlin material model. These results can be utilized to understand the extension and rupture mechanism of UV and has implications for interventions and surgeries, including balloon-angioplasty, bypass, and stenting.
Conflicts of interest
We declare that we have no conflicts of interest.
Acknowledgment
The authors acknowledge the
References
Cite this article
TY - JOUR AU - Alireza Karimi AU - Mahdi Navidbakhsh AU - Mansour Alizadeh AU - Ahmad Shojaei PY - 2014 DA - 2014/02/28 TI - A comparative study on the mechanical properties of the umbilical vein and umbilical artery under uniaxial loading JO - Artery Research SP - 51 EP - 56 VL - 8 IS - 2 SN - 1876-4401 UR - https://doi.org/10.1016/j.artres.2014.02.001 DO - 10.1016/j.artres.2014.02.001 ID - Karimi2014 ER -
